1 кг это масса кубика с водой

1 кг это масса кубика с водой

Деревянный кубик с ребром 10 см плавает частично погруженный в воду. Его начинают медленно погружать, действуя силой, направленной вертикально вниз. В таблице приведены значения модуля силы, под действием которой кубик находится в равновесии частично или полностью погруженный в воду. Выберите все верные утверждения на основании данных, приведенных в таблице.

№ опыта	1	2	3	4	5	6	7	8
Модуль силы, F, H	0,2	0,8	1,8	3,0	4,0	5,0	5,0	5,0

1) В опыте № 6 сила Архимеда, действующая на кубик, меньше, чем в опыте № 2.

2) В опыте № 7 кубик погружен в воду полностью.

3) Масса кубика равна 0,5 кг.

4) В опыте № 4 кубик погружен в воду на половину своего объема.

5) Плотность кубика равна 400 кг/м 3 .

Введём обозначения: — масса кубика, — длина его ребра, — погружённая в воду высота кубика, — плотность воды.

В равновесии силы, действующие на кубик, компенсируют друг друга:

1) В опыте № 6 сила больше, чем в опыте № 2, значит, и сила Архимеда тоже больше.

2) После опыта № 6 сила перестала меняться, сила Архимеда тоже, значит, кубик полностью погрузился в воду.

3) Установим массу кубика из опыта, с полностью погруженным кубиком:

4) В опыте № 4 глубина погружения была

5) Плотность кубика равна

Верными являются второе и третье утверждения.

Источник

1 кг это масса кубика с водой

Формулы, используемые в задачах по физике на плотность, массу и объем.

Название величины

Обозначение

Единицы измерения

Формула

Масса

m = p * V

Объем

V = m / p

Плотность

кг/м 3

p = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

Физика 7 класс: все формулы и определения КРУПНО на трех страницах

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см 3 ?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см 3

Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м 3 ) меньше плотности стали (ρ₁ = 7800 кг/м 3 ). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

Задача № 5. Определите плотность мела, если масса его куска объемом 20 см 3 равна 48 г. Выразите эту плотность в кг/м 3 и в г/см 3 .

Ответ: Плотность мела 2,4 г/см 3 , или 2400 кг/м 3 .

Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м 2 ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м 3 • 0,04 м 2 • 5 м = 160 кг.

Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K = а 3 = 216 см 3 . Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р: V_С = m_К / р = 91 см 3 . Следовательно, объем полости V_П = V_K — V_C = 125 см 3 . Поскольку 125 см 3 = (5 см) 3 , полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м 3

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?

1. Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
2. Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
3. Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
4. Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
5. Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
6. Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
7. Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

Конспект урока «Задачи на плотность, массу и объем с решением».

Источник

Условия плавания тел

О чем эта статья:

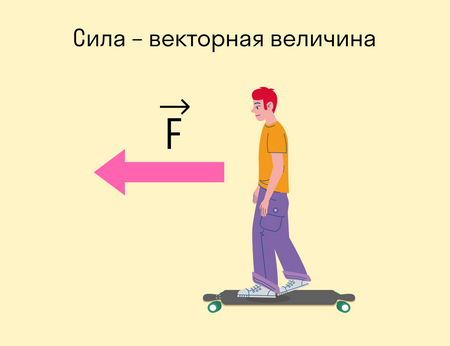
Сила: что это за величина

Перед тем, как разобраться в процессе плавания тел, нужно понять, что такое сила.

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — ее величество сила.

• Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.

Закон Архимеда

Этот закон известен преимущественно не своей формулировкой, а историей его возникновения.

Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом, не причиняя вреда самой короне. То есть, нельзя ее расплавить или в чем-нибудь растворить.

Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.

Это можно сделать по формуле плотности.

Формула плотности тела

ρ — плотность тела [кг/м^3]

m — масса тела [кг]

V — объем тела [м^3]

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.

Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (по легенде он даже не оделся).

Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.

На поверхность твердого тела, погруженного в жидкость или газ, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.

Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.

Сила Архимеда

ρ ж — плотность жидкости [кг/м^3]

V погр — объем погруженной части тела [м^3]

g — ускорение свободного падения [м/с^2]

На планете Земля: g = 9,8 м/с^2

А теперь давайте порешаем задачки.

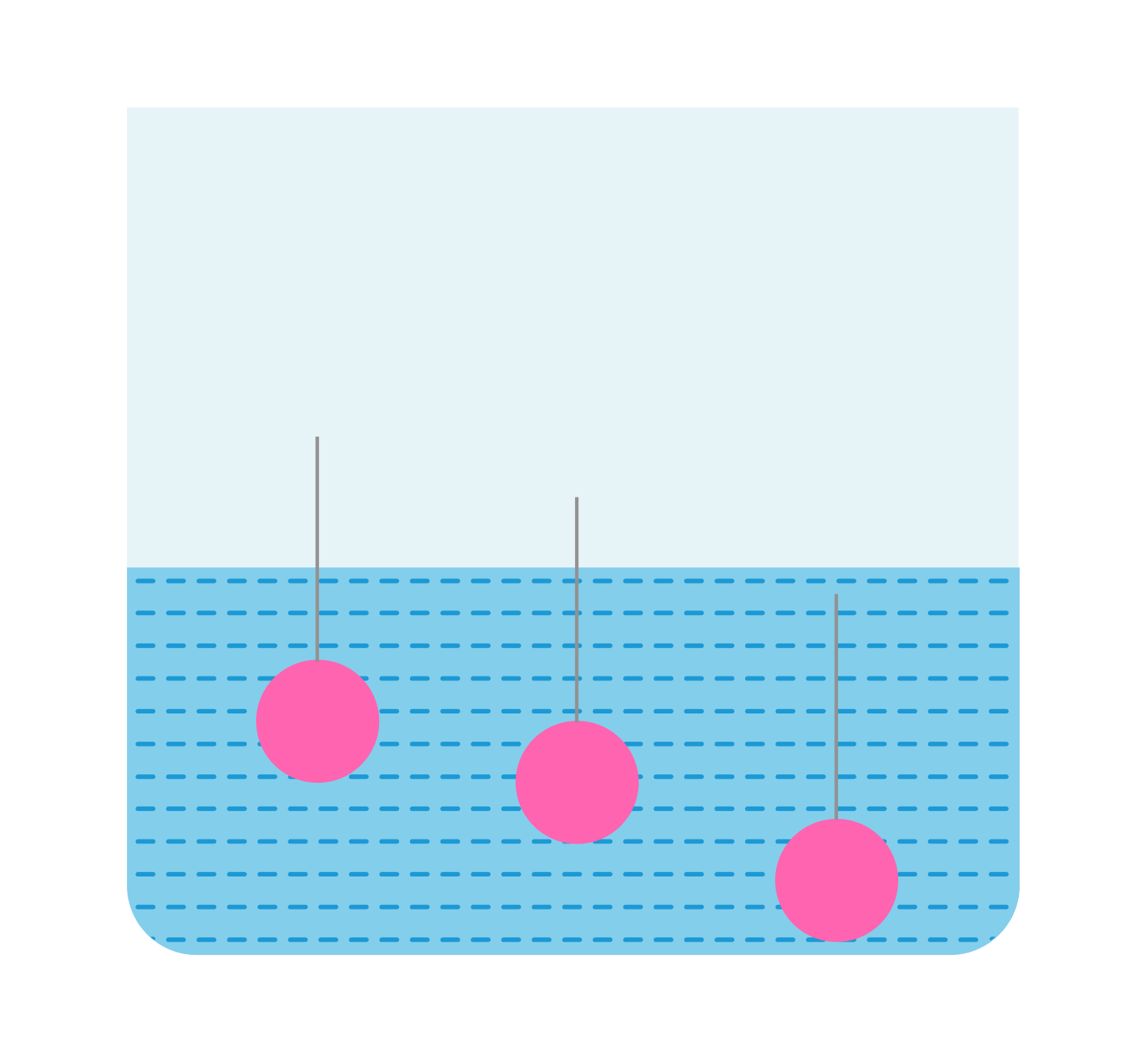
Задача 1

В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? (Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой).

Решение:

Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.

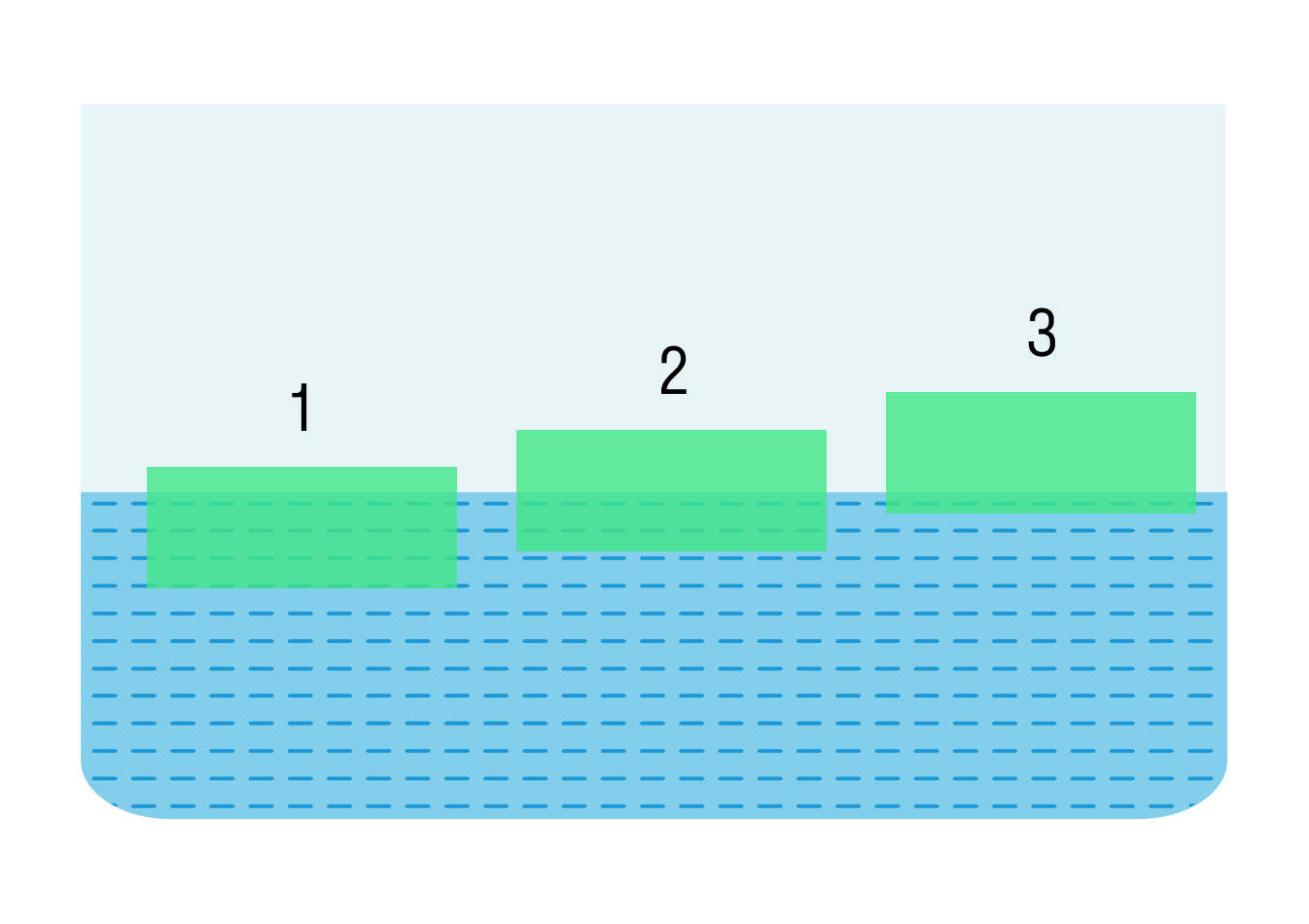
Задача 2

На поверхности воды плавают бруски из дерева, пробки и льда. Укажите, какой брусок из пробки, а какой изо льда? Какая существует зависимость между плотностью тела и объемом этого тела над водой?

Решение:

Чем меньше плотность тела, тем большая часть его находится над водой. Дерево плотнее пробки, а лед плотнее дерева. Значит изо льда — материал №1, а из пробки — №3.

Задача 3

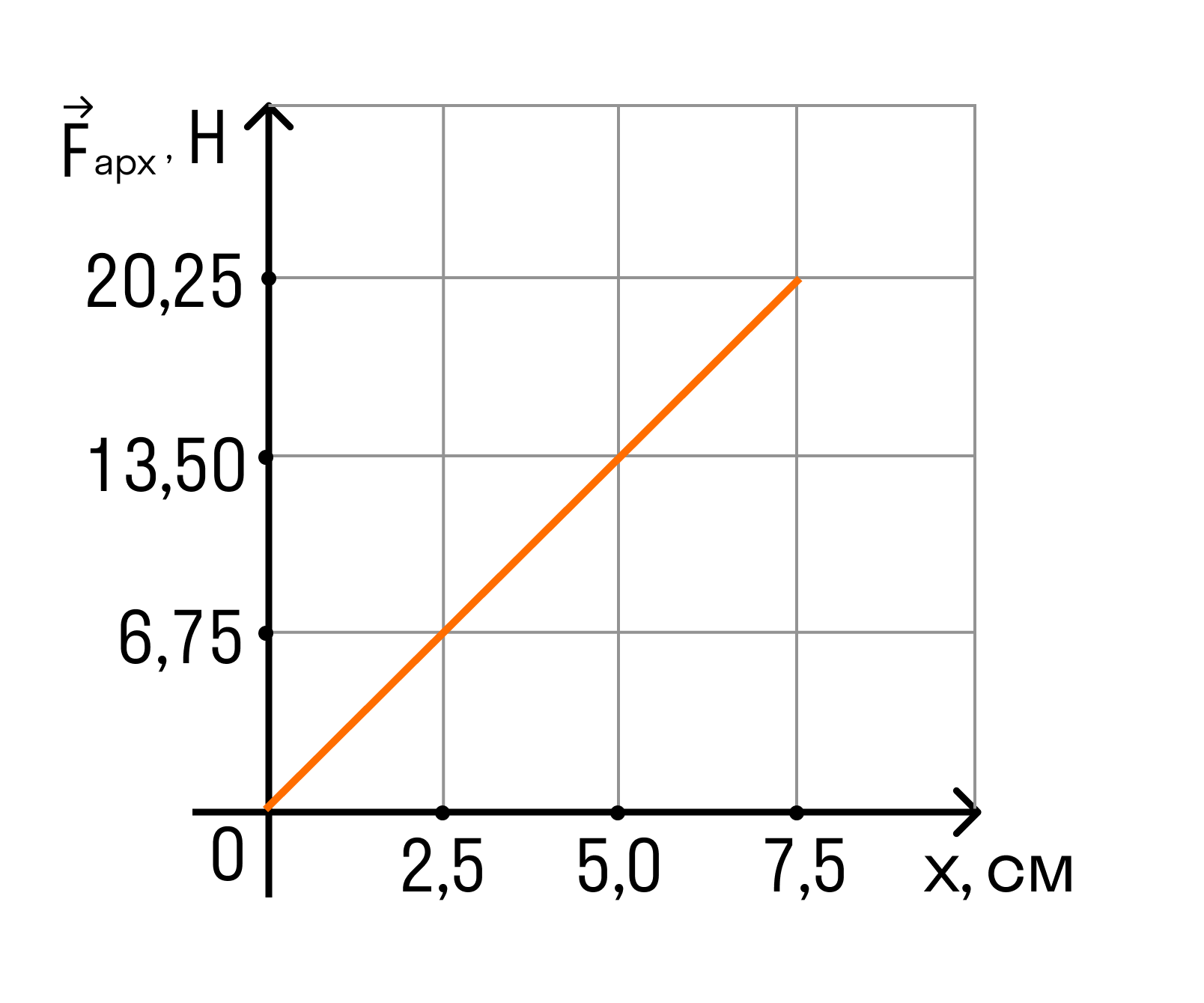
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с2.

Решение:

Сила Архимеда, действующая на кубик равна F_Арх = ρ_ж * g * V_погр

V — объём погруженной части кубика,

ρ — плотность жидкости.

Учитывая, что нижнее основание кубика всё время параллельно поверхности жидкости, можем записать:

а — длина стороны кубика.

ρ = F_Арх / (g * a 2 * x)

Рассматривая любую точку данного графика, получим:

ρ = F_Арх / (g * a 2 * x) = 20,25 / (10 * 7,5 * 10 -2 ) = 2700 кг/м3

Ответ: плотность жидкости равна 2700 кг/м3

Задача 4

В сосуде с водой, не касаясь стенок и дна, плавает деревянный кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? (Плотность сосны — 400 кг/м3.)

Решение:

В первом случае кубик плавает в воде, а это значит, что сила тяжести уравновешивается силой Архимеда:

F_Арх1 = mg = ρ_т * g * a 3 = 400 * 0,2 3 * 10 = 32 Н

После замены части кубика его средняя плотность станет равной

0,5 * 400 + 0,5 * 2400 = 1400 кг/м3

Получившаяся плотность больше плотности воды = 100 кг/м3. Это значит, что во втором случае кубик полностью погрузится в воду. Сила Архимеда в этом случае будет равна:

F_Арх2 = ρ_т * g * V_т = 1000 * 10 * 0,23 = 80 Н

Отсюда получаем, что сила Архимеда увеличится на 48 Н.

Ответ: сила Архимеда увеличится 48 Н

Плавание тел

Из закона Архимеда есть следствия об условиях плавания тел.

Условия плавания тел

Плавание внутри жидкости

Плавание на поверхности жидкости

Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.

Почему корабли не тонут?

Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.

В подводных лодках есть специальные резервуары, заполняемые водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.

Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.

Источник