Что такое ламинированная вода

ЛАМИНАРНОЕ ТЕЧЕНИЕ

Физический энциклопедический словарь. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1983 .

(от лат. lamina — пластинка) — упорядоченный режим течения вязкой жидкости (или газа), характеризующийся отсутствием перемешивания между соседними слоями жидкости. Условия, при к-рых может происходить устойчивое, т. е. не нарушающееся от случайных возмущений, Л. т., зависят от значения безразмерного Рейнольдса числа Re. Для каждого вида течения существует такое число R е Кр , наз. нижним критич. числом Рейнольдса, что при любом Re кp Л. т. является устойчивым и практически осуществляется; значение R е кр обычно определяется экспериментально. При R е>R е кр , принимая особые меры для предотвращения случайных возмущений, можно тоже получить Л. т., но оно не будет устойчивым и, когда возникнут возмущения, перейдёт в неупорядоченное турбулентное течение. Теоретически Л. т. изучаются с помощью Навье — Стокса уравнений движения вязкой жидкости. Точные решения этих ур-ний удаётся получить лишь в немногих частных случаях, и обычно при решении конкретных задач используют те или иные приближённые методы.

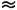
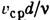
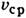
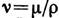
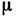
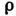
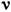
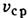
Представление об особенностях Л. т. даёт хорошо изученный случай движения в круглой цилиндрич. трубе. Для этого течения R е Кр 2200, где Re= ( — средняя по расходу скорость жидкости, d — диаметр трубы, — кинематич. коэф. вязкости, — динамич. коэф. вязкости, — плотность жидкости). Т. о., практически устойчивое Л. т. может иметь место или при сравнительно медленном течении достаточно вязкой жидкости или в очень тонких (капиллярных) трубках. Напр., для воды (=10 -6 м 2 /с при 20° С) устойчивое Л. т. с =1 м/с возможно лишь в трубках диаметром не более 2,2 мм.

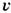
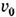
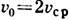
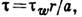
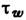
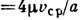
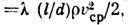
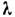
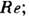
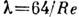
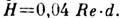
При Л. т. в неограниченно длинной трубе скорость в любом сечении трубы изменяется по закону —(1 — —r 2 / а 2 ), где а — радиус трубы, r — расстояние от оси, — осевая (численно максимальная) скорость течения; соответствующий параболич. профиль скоростей показан на рис. а. Напряжение трения изменяется вдоль радиуса по линейному закону где = — напряжение трения на стенке трубы. Для преодоления сил вязкого трения в трубе при равномерном движении должен иметь место продольный перепад давления, выражаемый обычно равенством P₁-P₂ где p₁ и р ₂ — давления в к.-н. двух поперечных сечениях, находящихся на расстоянии l друг от друга, — коэф. сопротивления, зависящий от для Л. т. . Секундный расход жидкости в трубе при Л. т. определяет Пуазейля закон. В трубах конечной длины описанное Л. т. устанавливается не сразу и в начале трубы имеется т. н. входной участок, на к-ром профиль скоростей постепенно преобразуется в параболический. Приближённо длина входного участка

Распределение скоростей по сечению трубы: а — при ламинарном течении; б — при турбулентном течении.

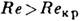
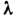
Когда при течение становится турбулентным, существенно изменяются структура потока, профиль скоростей (рис., 6 )и закон сопротивления, т. е. зависимость от Re (см. Гидродинамическое сопротивление).

Кроме труб Л. т. имеет место в слое смазки в подшипниках, вблизи поверхности тел, обтекаемых маловязкой жидкостью (см. Пограничный слой), при медленном обтекании тел малых размеров очень вязкой жидкостью (см., в частности, Стокса формула). Теория Л. т. применяется также в вискозиметрии, при изучении теплообмена в движущейся вязкой жидкости, при изучении движения капель и пузырьков в жидкой среде, при рассмотрении течений в тонких плёнках жидкости и при решении ряда др. задач физики и физ. химии.

Лит.: Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1954; Лойцянский Л. Г., Механика жидкости и газа, 6 изд., М., 1987; Тар г С. М., Основные задачи теории ламинарных течений, М.- Л., 1951; Слезкин Н. А., Динамика вязкой несжимаемой жидкости, М., 1955, гл. 4 — 11. С. М. Тарг.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Источник

Ламинарные фонтаны

Наткнулся на интересный вид фонтанов – Laminar jet, что в переводе на русский.. ламинарные фонтаны.

Вот ламинарный поток

А вот обычный турбулентный:

Наука это хорошо, но еще лучше, когда научные изыскания натыкаются на пытливый креативный ум, и люди начинают применять науку на пользу.

Фишка в том, что создав внутри пушки ламинарный поток и выведя его через дырку на конце получаем абсолютно ровную красивую струю воды.

поскольку струя ровная, она отлично проводит свет действуя как оптокабель. Поэтому такой фонтан запущенный с подсветкой выглядит просто офигенно ночью.

Самое главное – как и всё гениальное, сделать такой фонтан довольно просто, потребуется несколько труб, насос и пара сотен трубочек для коктейля. А, еще пара рук, растуших не из жопы.

Вот инструкция с которой можно начать:

Если хотите что-то серьезнее и интереснее, то шагайте на Нерусский форум

Я немного пояндексил и нашел даже у нас производителей такого чуда – Гидросервис. Тока дерут денег много.

Источник

Ламинарный режим движения жидкости

Движение жидкости, наблюдаемое при малых скоростях, при котором отдельные струйки жидкости движутся параллельно друг другу и оси потока, называют ламинарный режим движения жидкости.

В этой статье подробно описывается процесс ламинарного режима, переход в ламинарного режима из турбулентный, формула и закон этого режима и многое другое.

Очень наглядное представление о ламинарном режиме движения жидкости можно получить из опыта Рейнольдса. Подробное описание здесь.

Содержание статьи

Ламинарный режим движения в опытах

Жидкая среда вытекает из бака через прозрачную трубу и через кран уходит на слив. Таким образом жидкость течет с определенным небольшим и постоянным расходом.

На входе в трубу установлена тонкая трубочка по которой в центральную часть потока поступает подкрашенная среда.

При попадании краски в поток жидкости движущейся с небольшой скоростью красная краска будет двигаться ровной струйкой. Из этого опыта можно сделать вывод о слоистом течении жидкости, без перемешивания и вихреообразования.

Такой режим течения жидкости принято назыать ламинарным.

Рассмотрим основные закономерности ламинарного режима при равномерном движении в круглых трубах, ограничиваясь случаями, когда ось трубы горизонтальна.

При этом мы будем рассматривать уже сформировавшийся поток, т.е. поток на участке, начало которого находится от входного сечения трубы на расстоянии, обеспечивающем окончательный устойчивый вид распределения скоростей по сечению потока.

Имея ввиду, что ламинарный режим течения имеет слоистый(струйный) характер и происходит без перемешивания частиц, следует считать, что в ламинарном потоке будут иметь место только скорости, параллельные оси трубы, поперечные же скорости будут отсутствовать.

Можно представить себе, что в этом случае движущаяся жидкость как бы разделяется на бесконечно большое число бесконечно тонких цилиндрических слоев, параллельных оси трубопровода и движущихся один внутри другого с различными скоростями, увеличивающимися в направлении от стенок к оси трубы.

При этом скорость в слое, непосредственно соприкасающемся со стенками из-за эффекта прилипания равна нулю и достигает максимального значения в слое, движущемся по оси трубы.

Формула ламинарного режима течения

Принятая схема движения и введенные выше предположения позволяют теоретическим путем установить закон распределения скоростей в поперечном сечении потока при ламинарном режиме.

Для этого сделаем следующее. Обозначим внутренний радиус трубы через r и выберем начало координат в центре её поперечного сечения O, направив ось х по оси трубы, а ось z по вертикали.

Теперь выделим внутри трубы объем жидкости в виде цилиндра некоторого радиуса y длиной L и применим к нему уравнение Бернулли. Так как в следствии горизонтальности оси трубы z1=z2=0, то

где R – гидравлический радиус сечения выделенного цилиндрического объема = у/2

τ – единичная сила трения = — μ * dυ/dy

Подставляя значения R и τ в исходное уравнение получим

Задавая различные значения координаты y, можно вычислить скорости в любой точке сечения. Максимальная скорость, очевидно, будет при y=0, т.е. на оси трубы.

Для того, чтобы изобразить это уравнения графически, необходимо отложить в определенном масштабе от некоторой произвольной прямой АА скорости в виде отрезков, направленных по течению жидкости, и концы отрезков соединить плавной кривой.

Полученная кривая и представит собой кривую распределения скоростей в поперечном сечении потока.

График изменения силы трения τ по сечению выглядит совсем по другому. Таким образом, при ламинарном режиме в цилиндрической трубе скорости в поперечном сечении потока изменяются по параболическому закону, а касательные напряжения – по линейному.

Полученные результаты справедливы для участков труб с вполне развитым ламинарным течением. В действительности, жидкость, которая поступает в трубу, должна пройти от входного сечения определенный участок, прежде чем в трубе установится соответствующий ламинарному режиму параболический закон распределения скоростей.

Развитие ламинарного режима в трубе

Развитие ламинарного режима в трубе можно представить себе следующим образом. Пусть, например, жидкость входит в трубу из резервуара большого размеры, кромки входного отверстия которого хорошо закруглены.

В этом случае скорости во всех точках входного поперечного сечения будут практически одинаковы, за исключением очень тонкого, так называемого пристенного слоя(слоя вблизи стенок), в котором вследствие прилипания жидкости к стенкам происходит почти внезапное падение скорости до нуля. Поэтому кривая скоростей во входном сечении может быть представлена достаточно точно в виде отрезка прямой.

По мере удаления от входа, вследствие трения у стенок, слои жидкости, соседние с пограничным слоем, начинают затормаживаться, толщина этого слоя постепенно увеличивается, а движение в нем, наоборот, замедляется.

Центральная же часть потока (ядро течения), еще не захваченная трением, продолжает двигаться как одно целое, с примерно одинаковой для всех слоев скоростью, причем замедление движения в пристенном слое неизбежно вызывает увеличение скорости в ядре.

Таким образом, в середине трубы, в ядре, скорость течения все время возрастает, а у стенок, в растущем пограничном слое, уменьшается. Это происходит до тех пор, пока пограничный слой не захватит всего сечения потока и ядро не будет сведено к нулю. На этом формирование потока заканчивается, и кривая скоростей принимает обычную для ламинарного режима параболическую форму.

Переход от ламинарного течения к турбулентному

Ламинарное течения жидкости при некоторых условиях способно перейти в турбулентное. При повышении скорости течения потока слоистая структура потока начинает разрушаться, появляются волны и вихри, распространение которых в потоке говорит о нарастающем возмущении.

Постепенно количество вихрей начинает возрастать, и возрастает пока струйка не разобьется на множество перемешивающихся между собой более мелких струек.

Хаотичное движение таких мелких струек позволяет говорить о начале перехода ламинарного режима течения в турбулентное. С увеличением скорости ламинарное течение теряет свою устойчивость, при этом любые случайные небольшие возмущения, которые раньше вызывали только лишь малые колебания, начинают быстро развиваться.

Видео о ламинарном течении

В бытовом случае переход одного режима течения в другой можно отследить на примере струи дыма. Сначала частицы движутся практически параллельно по неизменяемым во времени траекториям. Дым практически неподвижен. Со временем в некоторых местах вдруг возникают крупные вихри, которые двигаются по хаотичным траекториям. Эти вихри распадаются на более маленькие, те – на еще более мелкие и так далее. В конце концов, дым практически смешивается с окружающим воздухом.

Источник