Эффект колеса для перемещения по воде

На цилиндрических колесах по воде

Когда в 1852 г. берлинский физик Магнус начинал свои опыты с цилиндрами, помещенными в воздушный поток, он, очевидно, и не предполагал, что результаты его исследований смогут найти практическое применение. Более того, он даже не смог объяснить обнаруженного явления, которое впоследствии получило его имя — эффект Магнуса. А явление это состоит в том, что если поместить цилиндр в воздушный поток (осью поперек направления потока) и начать вращать его, то появится какая-то сила, стремящаяся вытолкнуть цилиндр из потока. Причем эта сила действует перпендикулярно потоку, а ее направление зависит от того, в какую сторону вращается цилиндр.

Вскоре об эффекте Магнуса забыли, и забыли надолго. Только после исследований и Геттингенском аэродинамическом институте в 1923 г. немецкий инженер А. Флеттнер впервые попытался практически использовать вращающиеся цилиндры. Ему удалось построить судно — 900-тонную шхуну «Букау», на которой вместо мачт и парусов были установлены две цилиндрические колонны — роторы, приводимые во вращение двигателями мощностью по 20 л. с. (рис. 1).

Испытания показали полную техническую пригодность роторного судна, хотя как и у обычного парусного судна, скорость «Букау» зависела от скорости ветра. В экономическом отношении шхуна оказалась, конечно, менее выгодной, чем моторные суда, поэтому идея роторного судна заинтересовать судовладельцев не смогла, и вращающимися цилиндрами снова на некоторое время заниматься перестали.

Эффект Магнуса получил объяснение лишь после того, как Л. Прандтль в начале 90-х годов разработал теорию пограничного слоя. Было установлено, что при обтекании тела вязкой жидкостью (или газом) частицы жидкости, непосредственно соприкасающиеся с его поверхностью, как бы прилипают к ней и задерживают движение соседних частиц. Только на некотором удалении от поверхности тела скорость движения частиц жидкости снова становится равной скорости основного потока. Этот подторможенный слой жидкости Прандтль и назвал пограничным слоем.

Ну а в какой же связи находятся поперечная сила на вращающемся цилиндре и пограничный слой?

Сначала предположим, что цилиндр неподвижен. В самый начальный момент, когда еще не развился пограничный слой, цилиндр будет обтекаться сплошным, без отрыва, потоком жидкости. Скорости течения в точках А и С, где расходятся и вновь встречаются верхняя и нижняя части потока, оказываются равными нулю, а в точках В превышают скорость основного потока (рис. 2). В результате в точках А и С имеет место максимум давления, а в точках В максимальное разрежение, т. е. на участках АВ скорость течения возрастает, а на участках ВС уменьшается.

Образование на цилиндре пограничного слоя видоизменяет эту показанную на рис. 3 картину. На участках АВ частицы жидкости в пограничном слое движутся, преодолевая трение вдоль поверхности тела. На участках ВС, где разрежение постепенно переходит в давление, скорость частиц в пограничном слое уменьшается, происходит торможение пограничного слоя и возникает возвратное течение (рис. 4). Это течение как бы оттесняет внешний поток от поверхности цилиндра и приводит к отрыву пограничного слоя. В результате образуются вихри за цилиндром (рис. 5), которые размываются и уносятся потоком (рис. 6). Так как цилиндр обтекается симметрично с верхней и нижней сторон, никаких сил, направленных поперек потока, не будет.

Если же привести сам цилиндр во вращение, например, вправо (по часовой стрелке), то картина будет принципиально иной. Поскольку скорость частиц жидкости относительно верхней поверхности цилиндра уменьшится, здесь уменьшается и сопротивление трения (оно пропорционально квадрату скорости обтекания), частицы жидкости в пограничном слое продвинутся дальше по потоку, и точка отрыва пограничного слоя сместится в направлении к точке С.

На нижней поверхности цилиндра относительная скорость частиц жидкости увеличивается, поэтому возрастает сопротивление трения и точка отрыва пограничного слоя перемещается уже навстречу потоку, т. е. удаляется от точки С.

Симметрия обтекания нарушилась; следовательно, перераспределилось и давление по поверхности вращающегося цилиндра. Результатом этого перераспределения давлений и является поперечная сила, которая всегда направлена к той стороне, где направления вращения и потока совпадают.

При горизонтальном расположении цилиндров в воде, как это и должно иметь место на колесных судах, о которых мы будем говорить ниже, эта поперечная сила будет направлена вверх (подъемная сила на рис. 7, а) или вниз (топящая сила на рис. 7,6), в зависимости от направления вращения цнлиндров-колес.

Итак, мы рассмотрели эффект Магнуса и выяснили, что для его использования на «колесных» судах с целью получения силы, поднимающей корпус судна над водой, вращающиеся цилиндры должны быть полностью погружены в воду. Естественно, что для движения судна придется применять какие-го обычные движители. Таким образом получается, что погруженные цилиндры могут играть лишь роль подводных крыльев, но, по сравнению с крылом, цилиндр всегда будет иметь неизмеримо большее сопротивление и, следовательно, более низкое гидродинамическое качество (отношение подъемной силы к силе сопротивления). Максимальное гидродинамическое качество воащающегося цилиндра составляет К=1,3 и при использовании торцевых дисков К=2,28 (торцевые диски препятствуют перетеканию воды и как бы увеличивают эффективное удлинение цилиндра, а это приводит к росту величины подъемной силы (см. рис. 8). У подводного же крыла гидродинамическое качество оказывается выше в 10 и более раз.

Поэтому-то изобретатели и пытаются применить вращающиеся цилиндры, не погруженные в воду, а движущиеся по ее поверхности, что не имеет никакого отношения к эффекту Магнуса.

Еще в 30-е годы предлагалось установить цилиндры под днищем глиссирующего катера таким образом, чтобы они катились по поверхности воды. В 1939 г. англичане Ламбардини и Фиддерман после обширных исследований разработали проект катера (рис. 9), в котором подъемная сила создавалась на катящихся по воде шести цилиндрах. Они экстраполировали полученные экспериментальные данные на довольно высокую скорость, обеспечить которую не смогли из-за ограниченных возможностей лаборатории, где ставились опыты. Тем не менее, авторы сделали оптимистические выводы о несущей способности цилиндров.

В этом случае, как и в проекте Подорванова, делается ставка на ту поддерживающую силу, которая возникает на цилиндрах как на глиссирующих поверхностях. Однако, как показали экспериментальные исследования, гидродинамическое качество цилиндра всегда оказывается ниже, чем плоской пластины. Если у плоской пластины отогнута вверх по дуге круга только задняя часть, гидродинамическая подъемная сила сразу же существенно уменьшается. Как видно из построенного по результатам исследований В. П. Гребешова графика (рис. 10), на котором представлена зависимость обратного качества ε от угла атаки α, уменьшение К пластины с отгибом вверх при прочих равных условиях может составить около 25%. Значит, и поддерживать на воде такая выпуклая пластинка сможет не больший, а даже меньший вес, чем плоская (наоборот, если заднюю часть пластинки отогнуть вниз, подъемная сила возрастает, что и используется часто при проектировании катеров: днищу у транца придают небольшой отгиб вниз).

Глиссирующий цилиндр — та же пластина с отгибом вверх, только цилиндр находится в худших условиях обтекания, поэтому можно ожидать еще большего снижения гидродинамического качества. Вращение цилиндра вносит определенные изменения в структуру его обтекания, а потому и в характер развития сил на такой поверхности. Однако непременным условием, при котором возможно возникновение динамической подъемной силы, остается условие схода струй (срыва потока) в районе максимально погруженной точки (рис. 11). При этом в случае вращения цилиндра в направлении его движения действительно будет иметь место некоторое снижение сопротивления трения, если относительная скорость жидкости равна нулю, т. е. когда линейная скорость на поверхности вращающегося цилиндра равна скорости набегающего потока. Это равенство, как видно из эпюры распределения относительных касательных скоростей (рис. 11), выполняется не во всех точках погруженной поверхности, а потому будет снижаться только часть сопротивления трения. Заметим, что остальные виды сопротивления, характерные для тел, движущихся на поверхности воды, остаются. Что же касается подъемной силы, то расчеты по формулам работы [4] показывают уменьшение подъемной силы катящегося по поверхности воды цилиндра в два раза, по сравнению с эквивалентной плоской пластиной (этот результат относится к случаю бесконечного размаха сравниваемых поверхностей).

Таким образом, идея использовать вращающиеся цилиыдры или колеса для достижения наивысшей скорости на воде оказывается далеко не столь многообещающей, как уверяют некоторые изобретатели. При равной мощности механизмов и одинаковом весе «колесный» катер всегда будет проигрывать в скорости обычному глиссирующему, не говоря уже о катере на подводных крыльях. Но, может быть, важны амфибийные качества судна на колесах, его способность ходить по мелководью и выходить на берег? Именно с этой точки зрения американский ученый Таппорт оценивает колесные суда как перспективные. Однако до сих пор не было построено ни одного подобного судна. Многочисленные заявки изобретателей за последние 10 лет в большинстве своем повторяют одна другую, причем основное внимание в них до сих пор уделялось не конструктивным проработкам, а объяснению преимуществ будущих колесных аппаратов.

Небезынтересно упомянуть о некоторых применениях цилиндров на воде. Во время второй мировой войны губернатор штата Нью-Джерси (США) Чарльз Эдисон предложил использовать вращающееся с большой скоростью (катапультируемое с судна) цилиндрическое колесо, которое содержит катушку, для переброски каната на берег. Еще до войны в опытовом бассейне Д. Тейлора была начата серия испытаний зубчатых колес (рис. 12), которым сообщалась большая скорость вращения, после чего их сбрасывали на наклонную поверхность, подходившую по касательной к поверхности воды. Горизонтальная скорость, которую колесо развивало на наклонной плоскости, сохранялась и на некотором участке бассейна. Эти работы, приостановленные в годы войны, были вновь начаты в 1957 г. одной из американских компаний с целью использовать зубчатые колеса на высокоскоростных судах. Здесь уже ученые пытались использовать совсем другой принцип — принцип удара о поверхность воды. Таппорт предполагает, что зубчатые колеса могут найти применение, выполняя одновременно функции несущих поверхностей и движителей.

В последнее время и у нас в стране были проведены теоретические и экспериментальные исследования гидродинамических характеристик гладких и специальным образом профилированных круговых цилиндрических колес. Была испытана серия таких колес — свободно вращающихся и с приводом от двигателя. Эти испытания подтвердили предположение, что вращающиеся . колеса будут иметь значительно более низкое гидродинамическое качество, чем идентичная глиссирующая пластина или подводное крыло. Максимальное гидродинамическое качество испытанных колес оказалось немногим больше единицы, а это означает, что в экономическом отношении колесные аппараты будут значительно уступать глиссирующим судам, судам на подводных крыльях, судам на воздушной подушке и экранопланам.

Источник

О возможности повышения эффективности гребного колеса при высокой скорости судна

В настоящее время актуальны задачи освоения обширных территорий, в т.ч. районов крайнего Севера, с почти отсутствующей всесезонной дорожной сетью и портовой инфраструктурой при наличии неподготовленной морской береговой линии, болот, рек, озёр и др. Значительную роль в решении этих задач могут сыграть амфибийные средства на воздушной подушке, способные передвигаться как по суше, так и по заболоченным участкам, по мелководью, по глубокой воде [1] . Скорость таких судов при движении по воде должна по возможности превышать критическую (обычно порядка \(20\ldots 40 \;\text<км/ч>\) ), тогда энергозатраты на движение значительно снижаются, а дальность автономного передвижения повышается.

Для движителей таких судов традиционно применяются аэродинамические винты и водомёты [2] . Аэродинамические винты при характерных невысоких скоростях транспортного средства (судна) \(v_v\) относительно скорости отбрасываемого воздуха \(v_a\) имеют невысокую эффективность: отношение к потоку энергии \(\frac<1> <2>A \rho v_a^2\) мощности упора (тяги), связанной с силой отдачи от потока импульса \(\frac<1> <2>v_v A \rho v_a\) , сравнительно низкое ( \(A\) – характерная площадь сечения потока, \(\rho\) – плотность воздуха). Водомётные движители также не свободны от недостатков, в т.ч. [3–6]

• Меньший, по сравнению с винтом, КПД, из-за:
  • Необходимости перевозки, помимо собственно полезного груза, также и воды, находящейся в трубопроводе (в качестве рабочего тела);
  • Потери мощности из-за трения воды в трубопроводах;
  • Потери мощности из-за турбулентных завихрений потока воды в каналах водомёта.
• Затруднительность подачи воды сквозь днище судна к насосу, на эффективность которого будет влиять скорость движения судна относительно воды.
• Водозабор работает также как помпа и может затянуть со дна камни, песок, мусор. Это может забить систему охлаждения либо повредить импеллер и водовод.
• Водометный движитель разрушает дно прибрежной полосы
• Высока степень износа пары ротор-статор, так как эксплуатация производится на мелководье.
• Резкое и внезапное снижение КПД и упора при уменьшении скорости.

В качестве движителей судов применяются гребные колёса с неподвижными или поворотными лопатками (последние меняют угол наклона с частотой циклов поворота, равной частоте оборотов колеса) [7] . Они обеспечивают большой упор при малом заглублении, т.е. применимы на мелководье [8] . При малых скоростях судна \(\boldsymbol<\mathbf>_v\) они отличаются высокой эффективностью, определяемой как отношение мощности, связанной с силой от колеса \(\boldsymbol<\mathbf>\) , к механической мощности на валу,

где \(\boldsymbol<\mathbf>\) – вращательный момент на валу, \(\boldsymbol<\mathbf<ω>>\) − угловая скорость вращения колеса.

Длительное время их использование было ограничено [9] , что связано, во-первых, с недостаточной надёжностью поворотных лопаток, особенно при высоких скоростях вращения колеса, во-вторых, с тем, что при повышении скорости судна \(v_v\) до \(20\ldots30\;\text<км/ч>\) эффективность движителя \(\eta\) как с поворотными, так и с неподвижными лопатками обычно существенно снижается. Правда, в настоящее время, по-видимому, в связи с достижением предельных характеристик конкурирующих движителей для тихоходных мелкосидящих судов, отмечается некоторый рост интереса к колесным движителям [10; 11] .

Принципиальные ограничения эффективности колёсного движителя с неподвижными лопатками при высоких скоростях в литературе практически не описаны. Поэтому представляет значительный интерес изучение и устранение указанных ограничений с целью создания колёсного движителя, эффективного и на высоких, и на низких скоростях судна. Этому и посвящена данная работа.

Решалась система уравнений Навье-Стокса для динамики воздуха и воды как среды с переменной плотностью с учётом силы тяжести и с моделью турбулентности SST (вариант k-ω), в приближении изотермичности и малости числа Маха по сравнению с единицей [12] :

Здесь \(\alpha = \lbrace ,\rbrace\) – индекс, соответствующий воде или воздуху, \(r_<\alpha>\) – объемная доля соответствующей фазы, \(\rho\) – плотность, \(\boldsymbol<\mathbf>\) – вектор скорости среды, t – время, \(\mu_\) – эффективная вязкость среды, \(\mu\) – динамическая вязкость, \(\mu_\) – турбулентная вязкость, \(\rho_\) – референсная плотность, \(\rho_ = \rho_\) , \(\boldsymbol<\mathbf>\) – вектор ускорения свободного падения, \(k\) – турбулентная кинетическая энергия, \(\omega\) – удельная скорость диссипации, \(P_\) – возникновение турбулентности от вязких сил, S – инвариантная мера скорости деформации, \(F_<1>,F_<2>\) – смешивающие функции, \(y\) – расстояние до ближайшей стенки, \(\beta = 0.09\) , \(a_ <1>= \frac<5><9>\) , \(\beta_ <1>= 0.075\) , \(\sigma_ = 2\) , \(\sigma_ <\omega 1>= 2\) , \(a_ <2>= 0.44\) , \(\beta_ <2>= 0.0828\) , \(\sigma_ = 1\) , \(\sigma_ <\omega 2>= 1/0.856\) – модельные коэффициенты, \(\Phi_ <3>= F_<1>\Phi_ <1>+ \left( 1 — F_ <1>\right)\Phi_<2>\) , где \(\Phi = \lbrace a,\ \beta,\ \sigma_,\sigma_<\omega>\rbrace\) .

Зависимостью параметров от направления вдоль оси вращения пренебрегалось, что хорошо обосновано при характерных условиях, практически устраняющих нежелательные краевые эффекты: при наличии торцевых ограничителей и/или ширине колеса, превышающей ширину лопатки. На одной стороне прямоугольной расчётной области задавались скорости воды и воздуха, равные \(v_v\) , постоянное давление воздуха и распределение давления в воде, связанное с гравитацией \(p = \rho_ g (H — y)\) , где \(H\) – высота уровня воды, \(y\) – вертикальная координата, \(g\) – ускорение свободного падения, \(\rho_\) – плотность воды. На противоположной стороне задавалось свободное истечение с аналогичным распределением давления. На верхней границе задавалось свободное втекание и истечение воздуха \(\nabla \left(<\boldsymbol<\mathbf>\cdot\boldsymbol<\mathbf>>\right) = 0\) , \(p = p_<0>\) , где \(\boldsymbol<\mathbf>\) – скорость среды, \(p\) – давление на границе, \(p_<0>\) – атмосферное давление, \(\boldsymbol<\mathbf>\) – нормаль к границе; на нижней – непротекание \(\boldsymbol<\mathbf>\cdot\boldsymbol<\mathbf> = 0\) . Начальные условия соответствовали мгновенному появлению движущегося и вращающегося колеса в покоящихся (в земной системе координат) воде и воздухе. Расчёты производились до установления квазипериодического движения воды и воздуха (более одного оборота колеса).

Применялась подробная квазирегулярная многоблочная расчётная сетка, причём межлопаточные блоки скользили относительно периферийного блока, имеющего форму прямоугольника с вырезанным кругом.

Вычисления проводились с помощью программ ANSYS CFX, для уравнений переноса использовалась численная схема высокого разрешения, для шага по времени обратный метод Эйлера второго порядка, для турбулентности метод первого порядка. В качестве условия сходимости выбрана относительная среднеквадратичная погрешность меньше \(10^<- 4>\) . Сила \(\boldsymbol<\mathbf>\) вычислялась как интеграл горизонтальных проекций сил давления и поверхностного трения по всей площади контакта колеса с водой. В качестве параметров воды и воздуха (при \(25\;\text<⁰C>\) ) взяты данные из библиотеки материалов ANSYS. При вычислении КПД \(\eta\) , проводилось усреднение по времени периода входа лопаток (т.е. оборота колеса, делённого на число лопаток), чтобы сгладить выбросы, связанные с временным сдвигом между продольными импульсами и пиками момента торможения колеса.

Проводились вычислительные эксперименты по математическому моделированию различных вариантов геометрии неподвижных лопаток при скорости судна \(v_v\) от \(10\) до \(45\;\text<км/ч>\) и скорости вращения колеса, соответствующей максимальной окружной скорости \(v_\omega\) от \(10\) до \(60 \;\text<км/ч>\) . На приведённых ниже примерах диаметр колеса \(4\;\text<м>\) , скорость судна \(v_v = 45\;\text<км/ч>\) , \(v_\omega = 60\;\text<км/ч>\) .

Вначале был рассмотрен близкий к традиционному (паром ПКР-25, проекты ледоколов и др. [11; 13] ) вариант колеса с ободом и радиально расположенными лопатками (вариант I).

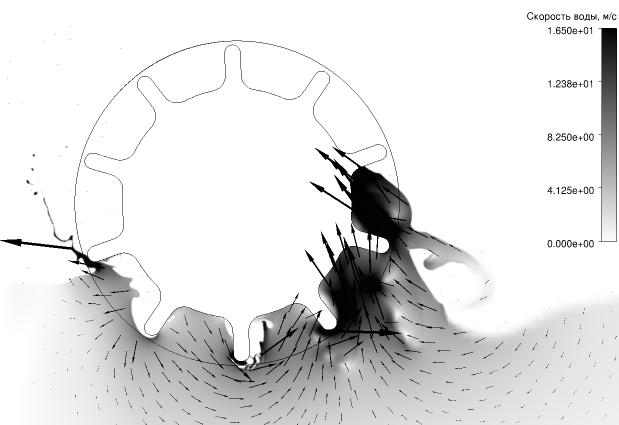
Результаты вычислений (рис. 1, 2) показали, что при указанной высокой скорости судна, во-первых, при входе лопатки в воду создаётся большое усилие, сильный всплеск, который гонит воду как назад, так и вперёд. Во-вторых, между лопатками при их нахождении под водой создаётся разрежение, которое формирует течение к колесу, в т.ч., сзади вперёд в земной системе координат. В-третьих, это разрежение замедляет слив воды при выходе лопаток, и вода ускоряется вверх относительно колеса, т.е. вперёд в земной системе координат. Т.о., при движении постоянно происходит захват части воды с ускорением вперёд до скорости порядка \(v_v\) . Другая часть воды получает при гребке скорость порядка скорости скольжения \(\Delta v = v_ω − v_v\) , но при необходимых высоких скоростях \(\Delta v \ll v_v\) . В результате, суммарный импульс, передающийся воде, в среднем направлен вперёд, а не назад, т.е. сила от колеса (упор) направлена назад относительно скорости судна. В результате, при высокой скорости (например, \(v_v = 45 \;\text<км/ч>\) ), эффективность движителя не просто мала, а отрицательна: колесо не ускоряет, а тормозит судно (рис. 2).

Рисунок 1: Распределение скоростей для варианта I Рисунок 2: Зависимости мгновенной эффективности η от угла поворота колеса φ для разных вариантов: а – вариант I, б – II, в – III. Стрелками обозначены выходящие за рамки части графиков

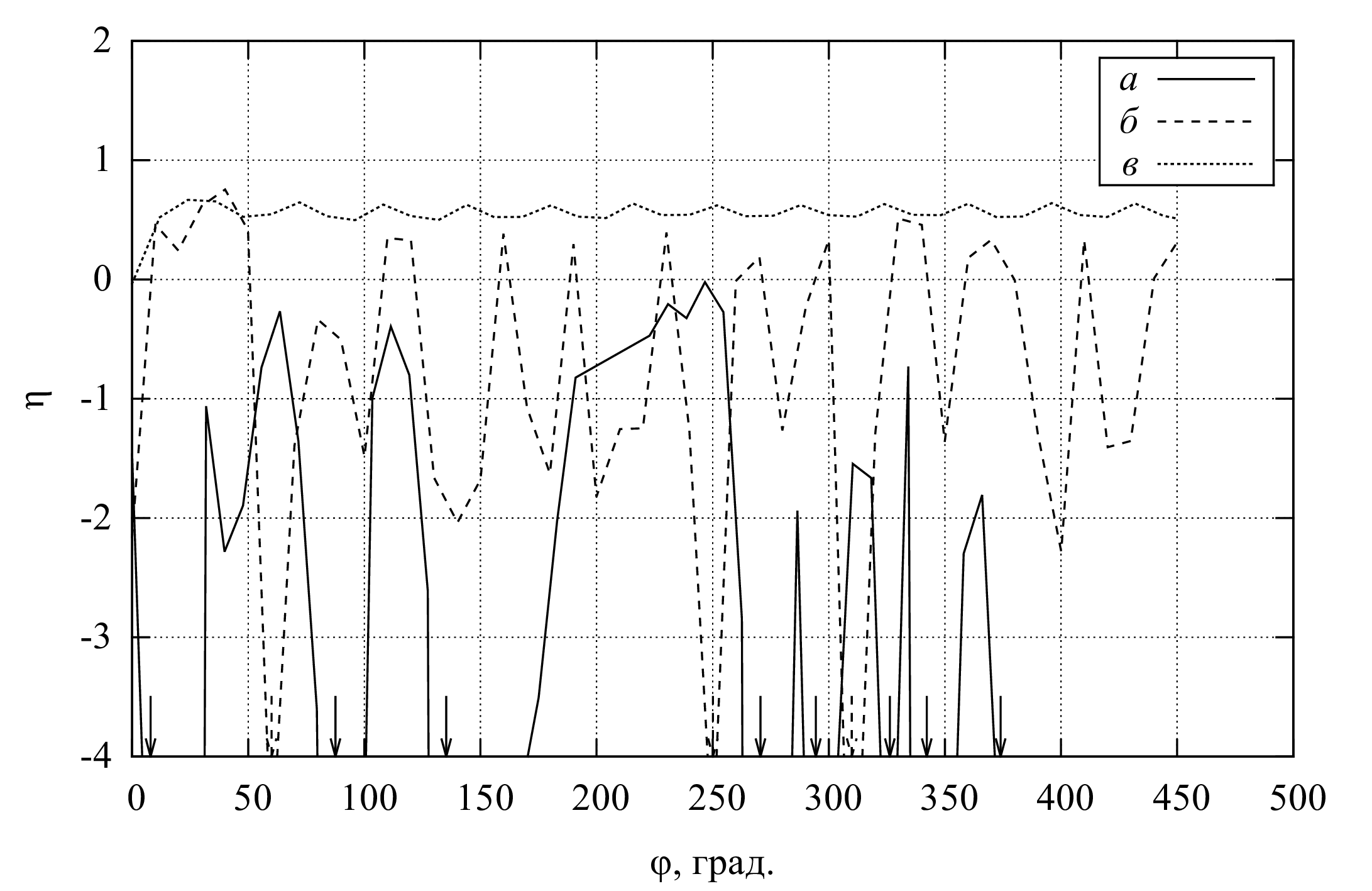
При снижении скорости \(v_v\) до \(10\ldots 15 \;\text<км/ч>\) , отрицательные эффекты уменьшаются, и расчётная эффективность \(\eta\) положительна. Отметим, что колёса с такой геометрией лопаток действительно применяются на тихоходных судах.

Другой вариант геометрии (рис. 3) характеризуется лопатками, отделёнными от обода, чтобы давление в межлопаточном пространстве выравнивалось за счёт поступления воздуха со стороны оси вращения (вариант II). По результатам вычислений видно, что эффекты, связанные с разрежением между лопатками, резко ослабляются. Однако при входе лопатки в воду также создаётся большое усилие, локально повышается давление, и формируется течение как назад, так и вперёд. Кроме того, часть воды недостаточно быстро стекает с лопаток и также ускоряется вперёд относительно земной системы координат. В результате при высоких скоростях судна (например, \(v_v = 45 \;\text<км/ч>\) ) эффективность движителя оказывается либо недопустимо мала, либо вовсе отрицательна (рис. 2).

Рисунок 3: Распределение скоростей для варианта II

В результате анализа вышеуказанного и проведения вариантных вычислений предложена новая геометрия лопаток (вариант III).

Она характеризуется, во-первых, тем, что вместо одиночных лопаток применяются двойные, тройные и пр. лопатки со щелями между ними, через которые вода после гребка сливается с таких лопаток быстрее, чем с одиночных лопаток. Это обеспечивает снижение массы ускоряемой вперёд воды и соответствующей отрицательной составляющей силы, действующей на колесо.

Во-вторых, тем, что внешняя лопатка имеет такой угол наклона относительно соответствующего радиуса, что при заданных \(v_v\) и \(v_\omega\) её внешний край входил бы в неподвижную воду под нулевым углом атаки. Это условие на угол атаки, характерное для оптимальных режимов практически всех лопаточных машин, обеспечивает снижение потерь импульса при входе лопатки в воду.

В-третьих, внутренние лопатки так расположены относительно внешних, что вода, текущая при гребке вдоль внешней лопатки со стороны повышенного давления, проходит по инерции мимо межлопаточной щели и попадает на поверхность внутренней лопатки. Это обеспечивает снижение потерь импульса при гребке из-за протекания воды по щелям.

В-четвёртых, углы наклона внутренних лопаток таковы, что стекающие с внешних лопаток потоки воды, имеющие значительную вертикальную составляющую, направляются внутренними лопатками горизонтально назад. Это снижает потери импульса на вертикальную составляющую.

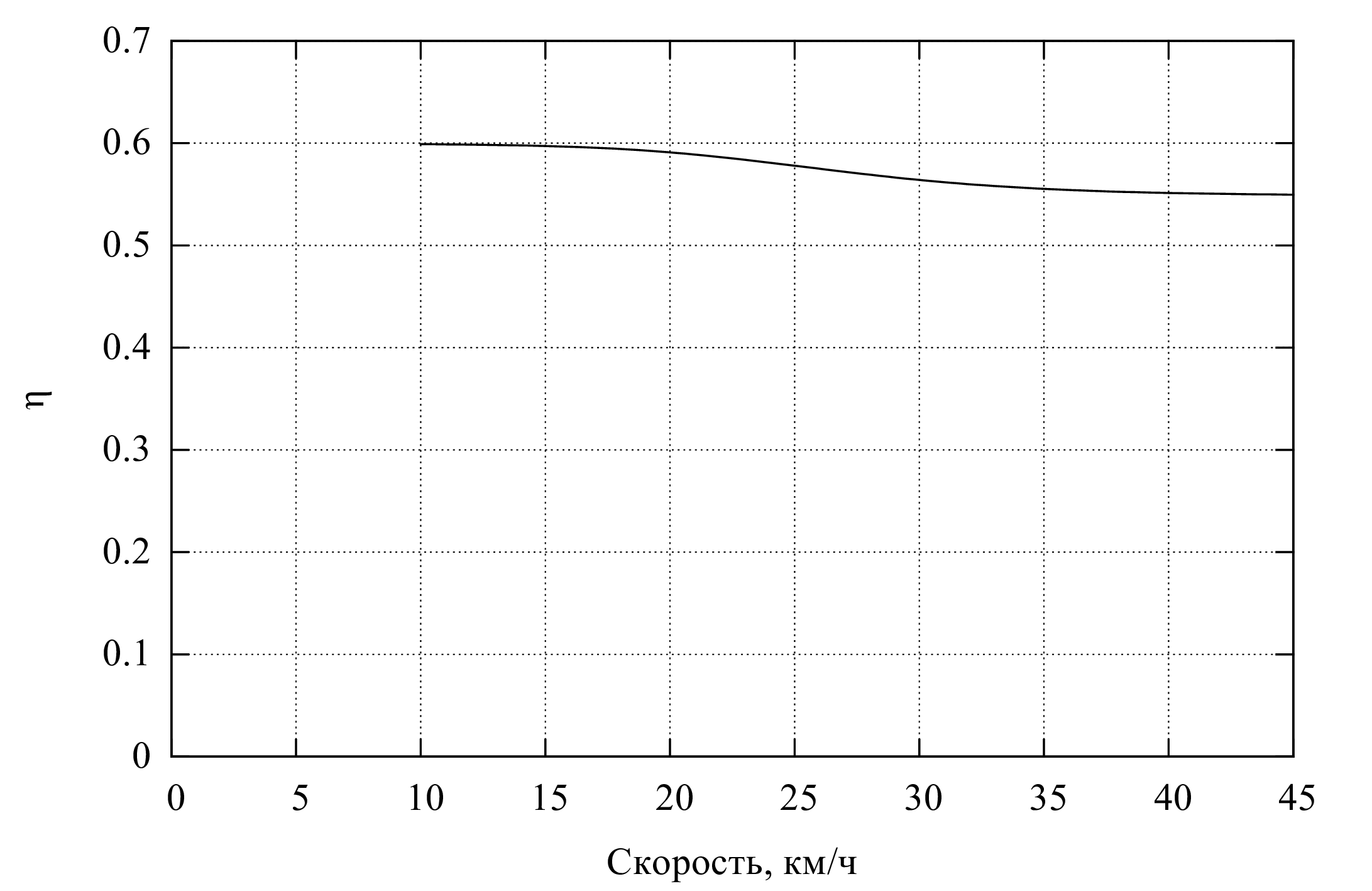
Результаты вычислений для лопаток с новой геометрией представлены на рис. 2, 4, 5.

Рисунок 4: Распределение скоростей для варианта III Рисунок 5: Зависимость КПД гребного колеса с разрезанными лопатками от скорости движения

Видно, что, несмотря на то, что воду в месте входа лопатки нельзя назвать неподвижной, погружение происходит без значительного всплеска и без локального повышения давления. Это минимизирует потери на вход.

Вода действительно меньше захватывается и быстрее сливается с нескольких коротких лопаток, чем с одной длинной, что снижает массу захватываемой воды и соответствующие потери импульса.

В то же время, при гребке протекание воды по щелям указанной геометрии затруднено из-за инерционности потоков воды, которые для этого должны поворачивать со значительными ускорениями. Поэтому, как и при сплошных лопатках, создаётся тянущее воду пониженное давление за разрезной лопаткой, а также толкающее воду повышенное давление перед лопаткой. В результате разрезные лопатки обеспечивают эффективность ускорения воды назад. Т.о., щели указанной геометрии не снижают создаваемый упор.

Вертикальная составляющая скорости движения воды, возникающая при гребке после взаимодействия с нижними лопатками, при взаимодействии с верхними лопатками эффективно преобразуется в горизонтальную, что увеличивает горизонтальную составляющую импульса, направленную назад относительно скорости судна, и повышает эффективность движителя.

Видно, что в результате принятых мер гребное колесо оказывается высокоэффективным движителем при высоких скоростях движения судна: значение \(\eta\) при скорости судна \(v_v = 45 \;\text<км/ч>\) достигает \(55\%\) . Кроме того, при меньших \(v_v\) оно оказывается даже несколько более эффективно– при условии сохранения вышеописанного соотношения между \(v_v\) и \(v_\omega\) , обеспечивающего плавный вход в воду (рис. 5).

Т.о., гребное колесо новой конструкции обладает качествами, критически важными для применения, в т.ч., в условиях Крайнего Севера. Значительный интерес представляет разработка движителей с применением гребных колес для вновь создаваемых судов амфибийного типа.

Список литературы

1. Попов С.Д. Проектирование и Комплексное Математическое Моделирование Судна На Воздушной Подушке Для Регионов Севера, Сибири и Арктического Континентального Шельфа. / С.Д. Попов, С.Н. Чувашев // Инженерный журнал: наука и инновации. – 2013. – № 3 (15). – P. 9.

2. Демешко Г.Ф. Проектирование Судов. Амфибийные Суда На Воздушной Подушке Книга 2 / Г.Ф. Демешко. – СПб: Судостроение, 1992. – 329 p.

3. Guard U.S.C. Non-standard boat operator’s handbook / U.S.C. Guard. – Washington: U.S. Dept of Transportation, 2006. – 170 p.

4. Баадер Х. Разъездные, Туристические и Спортивные Катера / Х. Баадер. – Л.: Судостроение, 1977. – 382 p.

5. Куликов С.В. Водометные Движители (Теория и Расчет). / С.В. Куликов, М.Ф. Храмкин. – Л.: Судостроение, 1980. – 312 p.

6. Водометный Движитель [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Водомётный_движитель.

7. Алферьев М.Я. Судовые Движители / М.Я. Алферьев. – М.: Мин. Речного флота СССР, 1947. – 662 p.

8. Гребное Колесо – Новый Вариант Мелководного Привода? [Электронный ресурс]. – Режим доступа: http://www.badger.ru/reviews/boats/31077.php.

9. Логвинович Э.Г. Колёсное Судно / Э.Г. Логвинович // Большая Советская Энциклопедия. – М.: Советская энциклопедия, 1969–1978.

10. Мерзляков В.И. Математическая Модель Комплекса Корпус–движитель Судна с Колесными Гребными Движителями / В.И. Мерзляков. – 2012. – № 1. – P. 56-61.

11. Конструкторское Бюро «Возрождение Колесных Судов» [Электронный ресурс]. – Режим доступа: http://www.wheelships.ru/.

12. Inc. A. ANSYS CFX-Solver Theory Guide / A. Inc. // Ansys CFX release 14 Help System. – 2012.

Источник