Энтальпия вода водяной пар

Теплофизические свойства водяного пара: плотность, теплоемкость, теплопроводность

Теплофизические свойства водяного пара при различных температурах на линии насыщения

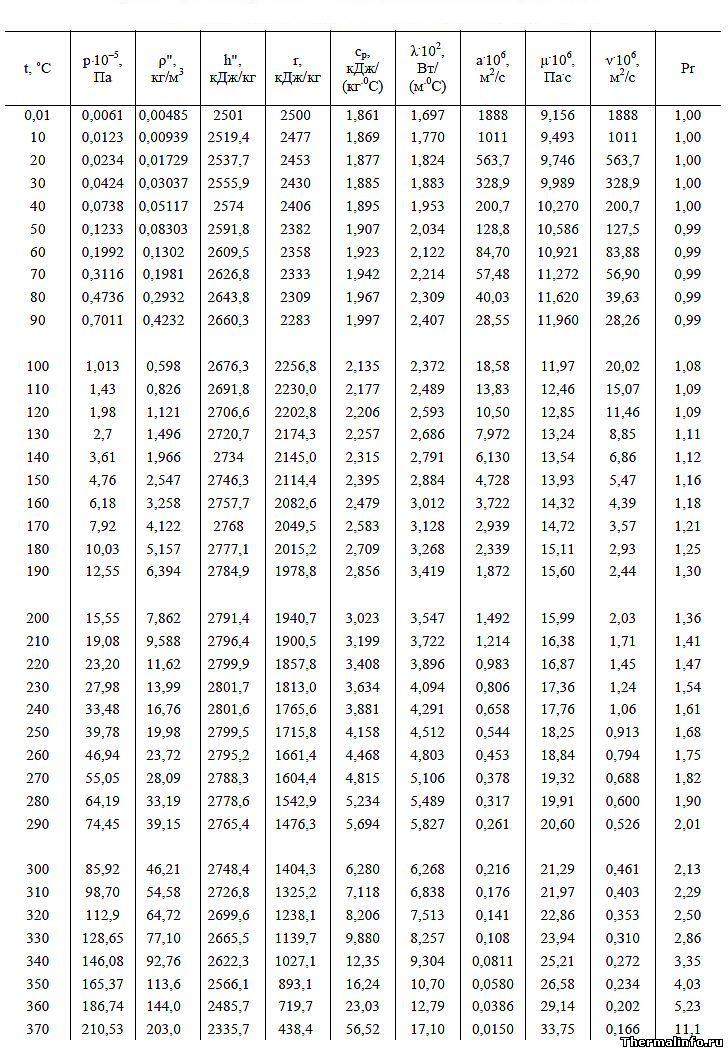
В таблице представлены теплофизические свойства водяного пара на линии насыщения в зависимости от температуры. Свойства пара приведены в таблице в интервале температуры от 0,01 до 370°С.

Каждой температуре соответствует давление, при котором водяной пар находится в состоянии насыщения. Например, при температуре водяного пара 200°С его давление составит величину 1,555 МПа или около 15,3 атм.

Удельная теплоемкость пара, теплопроводность и его динамическая вязкость увеличиваются по мере роста температуры. Также растет и плотность водяного пара. Водяной пар становится горячим, тяжелым и вязким, с высоким значением удельной теплоемкости, что положительно влияет на выбор пара в качестве теплоносителя в некоторых типах теплообменных аппаратов.

Например, по данным таблицы, удельная теплоемкость водяного пара C_p при температуре 20°С равна 1877 Дж/(кг·град), а при нагревании до 370°С теплоемкость пара увеличивается до значения 56520 Дж/(кг·град).

В таблице даны следующие теплофизические свойства водяного пара на линии насыщения:

• давление пара при указанной температуре p·10 -5 , Па;
• плотность пара ρ″, кг/м 3 ;
• удельная (массовая) энтальпия h″, кДж/кг;
• теплота парообразованияr, кДж/кг;
• удельная теплоемкость пара C_p, кДж/(кг·град);
• коэффициент теплопроводности λ·10 2 , Вт/(м·град);
• коэффициент температуропроводности a·10 6 , м 2 /с;
• вязкость динамическая μ·10 6 , Па·с;
• вязкость кинематическая ν·10 6 , м 2 /с;
• число Прандтля Pr.

Удельная теплота парообразования, энтальпия, коэффициент температуропроводности и кинематическая вязкость водяного пара при увеличении температуры снижаются. Динамическая вязкость и число Прандтля пара при этом увеличиваются.

Будьте внимательны! Теплопроводность в таблице указана в степени 10 2 . Не забудьте разделить на 100! Например, теплопроводность пара при температуре 100°С равна 0,02372 Вт/(м·град).

Теплопроводность водяного пара при различных температурах и давлениях

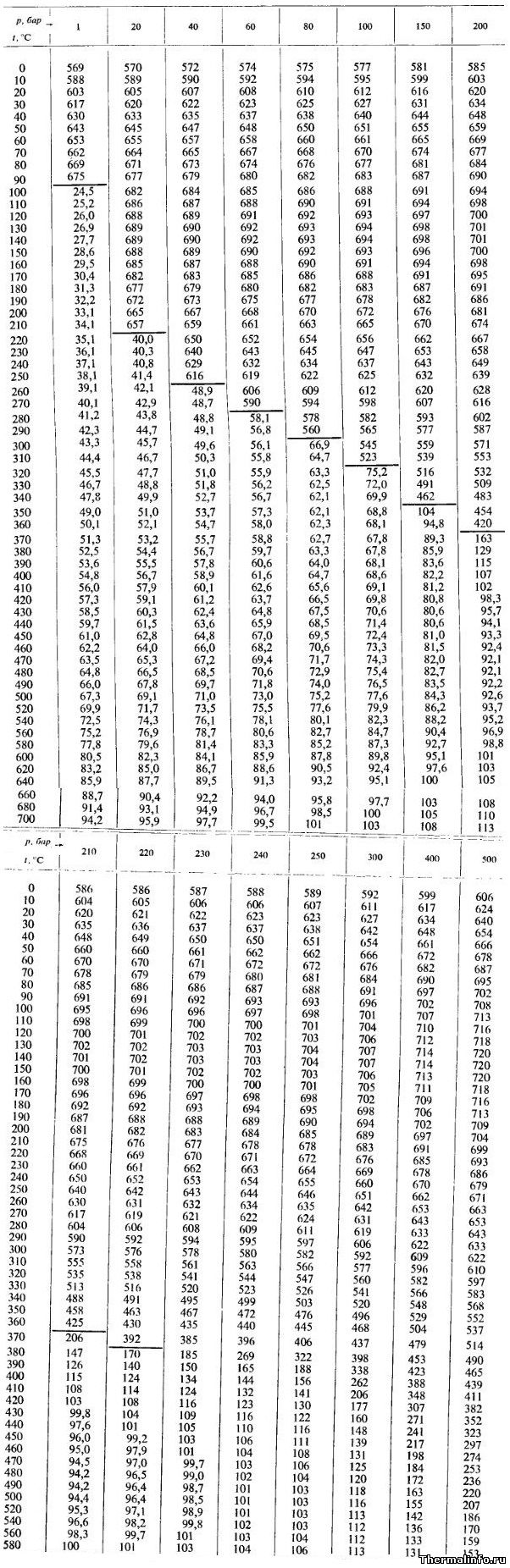
В таблице приведены значения теплопроводности воды и водяного пара при температурах от 0 до 700°С и давлении от 0,1 до 500 атм. Размерность теплопроводности Вт/(м·град).

Черта под значениями в таблице означает фазовый переход воды в пар, то есть цифры под чертой относятся к пару, а выше ее — к воде. По данным таблицы видно, что значение коэффициента теплопроводности воды и водяного пара увеличивается по мере роста давления.

Примечание: теплопроводность в таблице указана в степени 10 3 . Не забудьте разделить на 1000!

Теплопроводность водяного пара при высоких температурах

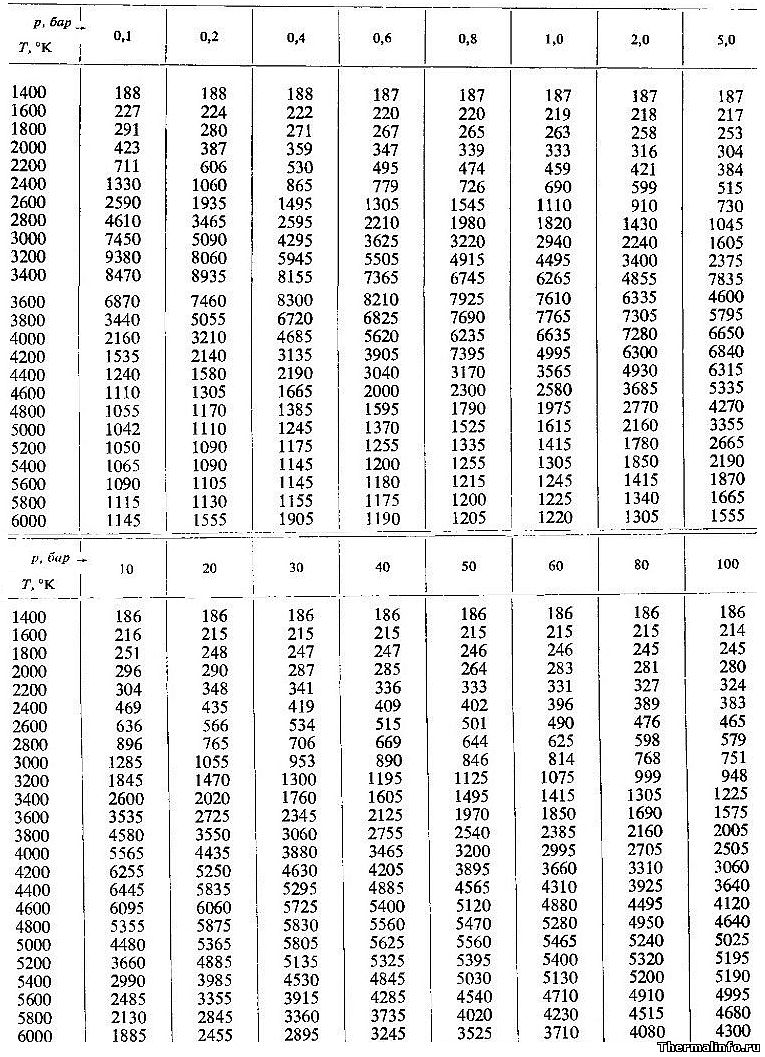
В таблице приведены значения теплопроводности диссоциированного водяного пара в размерности Вт/(м·град) при температурах от 1400 до 6000 K и давлении от 0,1 до 100 атм.

По данным таблицы, теплопроводность водяного пара при высоких температурах заметно увеличивается в области 3000…5000 К. При высоких значениях давления максимум коэффициента теплопроводности достигается при более высоких температурах.

Будьте внимательны! Теплопроводность в таблице указана в степени 10 3 . Не забудьте разделить на 1000!

Источник

Параметры пара

Свойства пара определяются его параметрами, то есть величинами, характеризующими состояние пара (давление, температура, степень сухости, энтальпия, теплосодержание и т. д.). Тепловая энергия подводится к паровой турбине при помощи водяного пара, являющегося носителем тепловой энергии (теплоносителем).

Насыщенный пар

Если нагревать воду в открытом сосуде, то температура ее будет постепенно повышаться, пока не достигнет примерно 100 0 С; после этого дальнейшее повышение температуры прекращается и начинается кипение воды, то есть бурный переход ее в парообразное состояние. Температура воды во время кипения остается одной и той же, так же как температура получающегося над водой пара; она равна точно 100 0 С при нормальном атмосферном давлении, равном давлению ртутного столба 760 мм высотой. Искусственно изменяя давление, можно изменять температуру кипения в очень широких пределах; при увеличении давления температура кипения повышается, при уменьшении давления – понижается.

Так, при давлении 0,02 ата (0,02 от атмосферного давления) вода кипит при 17,2 0 С, а при давлении 10 ата при 179 0 С.

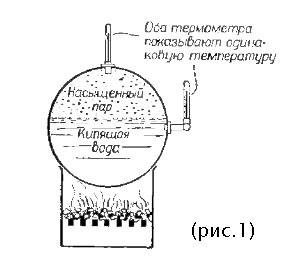
Температура пара над водой, из которой он получается (рис. 1), всегда равна температуре этой воды. Получающийся над водой пар называется насыщенный пар.

Определенной температуре насыщенного пара всегда соответствует определенное давление, и наоборот, определенному давлению всегда соответствует строго определенная температура.

В (таблице 1) приводится зависимость между температурой и давлением насыщенного пара.

Измерив термометром температуру насыщенного пара, можно по этой таблице определить его давление или, измерив давление, определить температуру.

При образовании пара в паровое пространство котла всегда попадают частицы воды, увлекаемые выделяющимся паром; особенно сильное увлажнение пара происходит в современных мощных котлах при работе их с большой нагрузкой. Кроме того, насыщенный пар обладает тем свойством, что при самом незначительном отнятии теплоты часть пара обращается в воду (конденсируется); вода в виде мельчайших капелек удерживается в паре. Таким образом, практически мы всегда имеем смесь сухого пара и воды (конденсата); такой пар называется влажный насыщенный пар. Так же как и у сухого насыщенного пара, температура влажного пара всегда соответствует его давлению.

Состав влажного пара принято выражать в весовых частях пара и воды. Вес сухого пара в 1 кг влажного пара называется или и обозначается буковой «х». Значение «х» обычно дают в сотых долях. Таким образом, если говорят, что у пара «х»=0,95, то это значит, что во влажном паре содержится по весу 95% сухого пара и 5% воды. При «х»=1 насыщенный пар носит название сухого насыщенного пара.

Один килограмм воды при своем испарении дает один килограмм пара; объем получающегося пара зависит от его давления, а следовательно, и от температуры. В противоположность воде, которая по сравнению с газами почти несжимаема, пар может сжиматься и расширяться в очень широких пределах.

Удельный объем, то есть объем 1 кг пара, при давлении 1 ата для сухого насыщенного пара равен 1,425 м 3 , то есть в 1725 раз больше объема 1 килограмма воды. При повышении давления удельный объем пара уменьшается, та как пар как упругое тело сжимается; так, при давлении 5 ата объем 1 кг сухого насыщенного пара уже равен только 0,3816 м 3 .

Энтальпия пара(теплосодержание) – практически определяется как количество тепла, которое нужно для поучения 1 кг пара данного состояния из 1 кг воды при 0 0 С, если нагрев происходит при постоянном давлении.

Понятно, что при одной и той же температуре энтальпии пара значительно больше, чем энтальпия воды. Для того чтобы нагреть 1 кг воды от 0 до 100 0 С, нужно затратить приблизительно 100 ккал тепла, так как теплоемкость воды равна приблизительно единице. Для того же, чтобы превратить эту воду в сухой насыщенный пар, нужно сообщить воде добавочно значительное количество теплоты, которое расходуется на преодоление внутренних сил сцепления между молекулами воды при переходе ее из жидкого состояния в парообразное и на совершение внешней работы расширения пара от начального объема v / (объем воды) до объема v // (объема пара).

Это добавочное количество теплоты называется теплота парообразования.

Следовательно, энтальпия сухого насыщенного пара будет определяться так:

i // =i / +r, ккал/кг,

где i // — полная теплота (энтальпия пара); i / — энтальпия воды при температуре кипения; r – теплота парообразования.

Например, при давлении 3 кг/см 3 теплосодержание 1 кг кипящей воды равно 133,4 ккал, а теплота парообразования равна 516,9 ккал/кг; отсюда энтальпия сухого насыщенного пара при давлении 3 кг/см 2 будет:

i // =133,4+516,9=650,3 ккал/кг (табл 2)

в сильной степени зависит от его степени сухости; с уменьшением степени сухости пара его энтальпия уменьшается.

Энтальпия влажного пара равна:

Эту формулу легко уяснить себе на следующем примере: допустим, что давление пара 5 кг/см 2 и степень сухости 0,9 иначе говоря, 1 кг этого пара содержит 0,1 кг воды и 0,9 кг сухого пара. По (табл 2) находим, что энтальпия воды при давлении 5 кг/см 2 равна округленно 152 ккал/кг, а энтальпия сухого пара 656 ккал/кг; так как влажный пар состоит из смеси сухого пара и воды, то энтальпия влажного пара в данном случае будет равна:

Следовательно, энтальпия влажного пара будет в этом случае примерно на 50 ккал/кг меньше, чем сухого насыщенного пара того же давления.

Перегретый пар

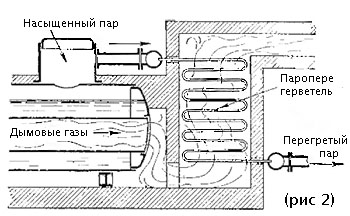
Если насыщенный пар отвести от поверхности испарения воды в котле и продолжать нагревать его отдельно, то температура пара будет подниматься и объем его увеличиваться. Устройство, в котором пар подогревается (пароперегреватель), сообщается с паровым пространством котла (рис 2). Пар, температура которого выше температуры кипения воды при том же давлении, называется . Если давление пара равно 25 ата, а температура его 425 0 С, то он прегрет на 425 – 222,9 = 202,1 0 С, так как давлению 25 ата соответствует температура насыщенного пара, равная 222,9 0 С (табл 2)

Энтальпия перегретого пара

Следовательно, она превышает энтальпию сухого насыщенного пара того же давления на величину, выражающую собой количество теплоты, дополнительно сообщенное пару при перегреве; это количество теплоты равно:

а=ср(t2 – t1), ккал/кг,

где ср – средняя теплоемкость 1 кг пара при постоянном давлении. Ее величина зависит от давления и температуры пара; в (табл. 3) даны значения ср для некоторых температур и давлений;

t1 – температура насыщенного пара; t2 – температура перегретого пара.

Энтальпии перегретого пара для некоторых давлений и температур приведены в (табл. 4).

Перегревая свежий пар, мы сообщаем ему дополнительную теплоты, то есть увеличиваем начальную энтальпию. Это приводит к увеличению использованного теплопадения и повышению экономического к.п.д. установки работающей на перегретом паре. Кроме того, перегретый пар при движении в паропроводах не конденсируется в воду, так как конденсация может начаться только с момента, когда температура перегретого пара понизиться на столько, что он перейдет в насыщенное состояние. Отсутствие конденсации свежего пара особенно важно для паровых турбин, вода, скопившаяся в паропроводе и увлеченная паром в турбину, легко может разрушить лопатки турбины.

Преимущество перегретого пара настолько значительны и выгодность его применения настолько велика, что современные турбинные установки работают почти исключительно перегретым паром.

В настоящее время большинство тепловых электростанций строится с параметрами пара свыше 130 – 150 ата и свыше 565 0 С. В дальнейшем для самых мощных блоков предполагается по мере освоения новых жаростойких сталей повысить параметры до 300 ата и 656 0 С.

При расширении перегретого пара его температура понижается, по достижении температуры насыщения перегретый пар проходит через состояние сухого насыщенного пара и превращается во влажный пар.

Источник

Водяной пар. Влажный воздух

Cтатистика главы

Количество разделов	4
Количество задач	165

Содержание главы

Примеры решений задач

Данные примеры задач, относятся к предмету «Техническая термодинамика».

Задача #6611

Определить температуру, удельный объем, плотность, энтальпию и энтропию сухого насыщенного пара при давлении p = 1 МПа.

По справочной таблице (насыщенный водяной пар) при p = 1 МПа находим параметры пара:

υ ’ ’ = 0,1946 м 3 к г

ρ ’ ’ = 5,139 к г м 3

i ’ ’ = 2778 к Д ж к г

s ’ ’ = 6,587 к Д ж к г × К

Ответ: не указан.

Задача #66110

Водяной пар имеет параметры p = 3 МПа, t = 400 ℃.

Определить значения остальных параметров.

Так как температура пара больше критической, то пар приведенных параметров перегретый. По справочной таблице перегретого пара находим:

υ = 0,0993 м 3 к г

i = 3229 к Д ж к г

s = 6,919 к Д ж к г × К

ρ = 1 υ = 1 0,0993 = 10,07 к г м 3

Внутреннюю энергию пара определяем из общей зависимости

u = i — p υ = 3229 — 3 × 10 3 × 0,0993 = 2931,1 к Д ж к г

Ответ: не указан.

Задача #66111

Определить количество теплоты, затрачиваемой на перегрев 1 кг сухого насыщенного пара при 9 МПа до 500 ℃.

Из справочной таблицы (при 9 МПа до 500 ℃) находим:

— удельная энтальпия сухого насыщенного пара

i ’ ’ = 2743 к Д ж к г

— удельная энтальпия перегретого пара

i = 3386 к Д ж к г

Следовательно, теплота перегрева пара

q п = i — i п = 3386 — 2743 = 643 к Д ж к г

Ответ: q_п = 643 кДж/кг.

Задача #66112

В паровом котле объемом V = 12 м 3 находятся 1800 кг воды и пара при давлении 11 МПа и температуре насыщения.

Определить массы воды и сухого насыщенного пара, находящиеся в котле.

Обозначим массы воды и пара соответственно через M_в и M_п (в кг). Удельный объем кипящей воды равен υ’ м 3 /кг, а удельный объем сухого насыщенного пара — υ’’ м 3 /кг. Следовательно, объем, занимаемый водой,

а объем, занимаемый паром,

V = M в υ ’ + M п υ ’ ’

V = M — M п υ ’ + M п υ ’ ’ = M υ ’ + M п υ ’ ’ — υ ’

Из этого выражения

M п = V — M υ ’ υ ’ ’ — υ ’

Из справочной таблицы получаем:

υ ’ = 0,001489 м 3 к г

υ ’ ’ = 0,01598 м 3 к г

Следовательно, масса пара

M п = 12 — 1800 × 0,001489 0,01598 — 0,001489 = 643,2 к г

M в = 1800 — 643,2 = 1156,8 к г

Ответ: M_п = 643,2 кг; M_в = 1156,8 кг.

Задача #6612

Найти давление, удельный объем и плотность воды, если она находится в состоянии кипения и температура ее равна 250 ℃.

По справочной таблице при 250 ℃ найдем параметры воды:

υ ’ = 0,0012512 м 3 к г

ρ ’ = 1 υ ’ = 1 0,0012512 = 799,2 к г м 3

Ответ: не указан.

Задача #6613

Манометр парового котла показывает давление 0,2 МПа. Показание барометра 0,103 МПа (776 мм рт. ст.).

Считая пар сухим насыщенным, определить его температуру, удельный объем и энтальпию.

Абсолютное давление пара в паровом котле

p = 0,103 + 0,2 = 0,203 М П а

По справочной таблице (насыщенный водяной пар) находим параметры пара:

Интерполируя, получаем для р = 0,303 МПа.

t н = 133,54 + 0,112 × 3 = 133,88 ℃

— удельный объем пара

υ ’ ’ = 0,5928 м 3 к г

— удельную энтальпию пара

i ’ ’ = 2726 к Д ж к г

Задача #6614

Определить состояние водяного пара, если давление его p = 0,5 МПа, а температура t = 172 ℃.

Давлению 0,5 МПа соответствует температура насыщенного пара

Так как эта температура ниже заданной в условии, то пар перегрет, причем перегрев составляет

t — t н = 172 — 151,8 = 20,2 ℃

Ответ: пар перегрет.

Задача #6615

Определить состояние водяного пара, если давление его p = 0,6 МПа, а удельный объем υ = 0,3 м 3 /кг.

Давлению 0,6 МПа соответствует удельный объем сухого насыщенного пара

υ ’ ’ = 0,3156 м 3 к г

Так как для заданного состояния υ’’ > υ, то пар является влажным.

Степень сухости пара

x = υ x — υ ’ υ ’ ’ — υ ’ = 0,3 — 0,0011 0,3156 × 0,0011 = 0,95

или по приближенной формуле

x = υ x υ ’ ’ = 0,3 0,3156 = 0,95

Таким образом, расчет по приближенной формуле для данного случая весьма точен.

Ответ: пар влажный.

Задача #6616

Определить внутреннюю энергию сухого насыщенного пара при p = 1,5 МПа.

Внутренняя энергия для сухого насыщенного пара

По справочной таблице при p = 1,5 МПа определим параметры сухого насыщенного пара:

i ’ ’ = 2792 к Д ж к г

υ ’ ’ = 0,1317 м 3 к г

u ’ ’ = 2792 — 1,5 × 10 3 × 0,1317 = 2594 к Д ж к г

Ответ: u’’ = 2594 кДж/кг.

Задача #6617

Определить энтальпию и внутреннюю энергию влажного насыщенного пара при p = 1,3 МПа и степени сухости пара x = 0,98.

Энтальпия влажного пара

По справочным таблицам при p = 1,3 МПа находим:

i ’ = 814,5 к Д ж к г

— скрытая теплота парообразования

r = 1973 к Д ж к г

— удельный объем сухого насыщенного пара

υ ’ ’ = 0,1512 м 3 к г

i x = 814,5 + 1973 × 0,98 = 2748,5 к Д ж к г

Удельный объем влажного пара

υ x = υ ’ ’ x = 0,1512 × 0,98 = 0,148 м 3 к г

Внутренняя энергия влажного насыщенного пара

u x = i x — p υ x = 2748,5 — 1,3 × 10 3 × 0,148 = 2556,1 к Д ж к г

Ответ: i_x = 2748,5 кДж/кг; u_x = 2556,1 кДж/кг.

Задача #6618

Найти энтропию влажного насыщенного пара p = 2,4 МПа и x = 0,8.

Энтальпия влажного насыщенного пара

s x = s ’ + s ’ ’ — s ’ x

По справочной таблице при p = 2,4 МПа находим:

s ’ = 2,534 к Д ж к г × К

— энтропию сухого насыщенного пара

s ’ ’ = 6,272 к Д ж к г × К

s x = 2,534 + 6,272 — 2,534 × 0,8 = 5,524 к Д ж к г × К

Ответ: 5,524 кДж/(кг × К).

Задача #6619

Найти массу, внутреннюю энергию, энтальпию и энтропию 6 м 3 насыщенного водяного пара при давлении p = 1,2 МПа и сухости пара x = 0,9.

По таблицу водяного пара, при p = 1,2 МПа, находим параметры пара и воды:

— удельный объем пара

υ ’ ’ = 0,1633 м 3 к г

i ’ = 798,3 к Д ж к г

— скрытая теплота парообразования

r = 1987 к Д ж к г

s ’ = 2,216 к Д ж к г × К

s ’ ’ = 6,523 к Д ж к г × К

Удельный объем влажного пара

υ x = υ ’ ’ x = 0,1633 × 0,9 = 0,147 м 3 к г

M = V υ x = 6 0,147 = 40,8 к г

Удельная энтальпия влажного пара

i x = i ’ + r x = 798,3 + 1987 × 0,9 = 2586,3 к Д ж к г

I x = M i x = 40,8 × 2586,3 = 105521 к Д ж

Внутренняя энергия пара

U x = M i x — p υ x = 40,8 × 2586,3 — 1,2 × 10 3 × 0,147 = 98324 к Д ж

S x = M s x = M s ’ + s ’ ’ — s ’ x =

= 40 × 2,216 + 6,523 — 2,216 × 0,9 = 40 × 6,092 = 248,6 к Д ж К

Ответ: не указан.

Задача #6621

Задано состояние пара: p = 1,6 МПа; x = 0,96.

Определить остальные параметры, пользуясь диаграммой, и сравнить их со значениями этих же параметров, вычисленных с помощью таблиц водяного пара и соответствующих формул.

На диаграмме is находим точку A, характеризующую данное состояние (рис.). Проектируя ее соответственно на ось ординат и ось абсцисс, находим значение:

i x = 2716 к Д ж к г

s x = 6,26 к Д ж к г × К

Величина удельного объема пара определяется по значению изохоры, проходящей через точку A:

υ x = 0,12 м 3 к г

Для определения температуры пара нужно от точки A подняться по изобаре p = 1,6 МПа до верхней пограничной кривой (точка B). Через эту точку проходит изотерма

эта температура и является температурой насыщенного пара при давлении 1,6 МПа.

Сопоставим полученные значения со значениями этих же параметров, вычисленных при помощи таблиц водяного пара и соответствующих формул. По справочной таблице для при давлении 1,6 МПа находим:

υ ’ ’ = 0,1238 м 3 к г

i ’ = 858,3 к Д ж к г

r = 1935 к Д ж к г

s ’ = 2,344 к Д ж к г × К

s ’ ’ = 6,422 к Д ж к г × К

Энтальпия влажного пара

i x = i ’ + r x = 858,3 + 0,96 × 1935 = 2715,9 к Д ж к г

Энтропия влажного пара

s x = s ’ + s ’ ’ — s ’ x = 2,344 + 6,422 — 2,344 × 0,96 = 6,2589 к Д ж к г × К

Удельный объем влажного пара

υ x = υ ’ ’ x = 0,1238 × 0,96 = 0,1188 м 3 к г

Как видно, совпадение значений параметров вполне удовлетворительное.

Ответ: не указан.

Задача #6622

В закрытом сосуде содержится 1 м 3 сухого насыщенного водяного пара при давлении 1 МПа.

Определить давление, степень сухости пара и количество отданной им теплоты, если он охладился до 60 ℃.

Пользуясь справочной таблицей, получаем при t₂ = 60 ℃ давление пара

p = 0,019917 М П а

Так как процесс происходит при постоянном объеме, то

υ 1 = υ 2 = υ 1 ’ ’ = 0,1946 м 3 к г

Пользуясь таблицей, находим,

υ 2 ’ ’ = 7,678 м 3 к г

и таким образом

x 2 = 0,1946 7,678 = 0,0253

Количество теплоты в изохорном процессе

Определяем значения внутренней энергии пара в начале и в конце процесса:

u 1 = i 1 — p 1 υ 1 = 2778 — 1 × 10 3 × 0,1946 = 2583,4 к Д ж к г

i 2 = i 2 ’ + r x 2 = 251,2 + 2358,8 × 0,0258 = 310,8 к Д ж к г

u 2 = i 2 — p 2 υ 2 = 310,8 — 0,019917 × 10 3 × 0,1946 = 306,9 к Д ж к г

q υ = 306,9 — 2583,4 = — 2276,5 к Д ж к г

Так как в рассматриваемом процессе участвует 1 м 3 пара и плотность его по таблице при p = 1 МПа

ρ = 5,139 к г м 3

q υ ’ = ρ q υ = 5,139 × — 2276,5 = — 11699 к Д ж к г

Ответ: q’_υ = -11699 кДж/кг.

Задача #6631

В закрытом сосуде содержится 1 м 3 сухого насыщенного водяного пара при давлении 1 МПа.

Определить давление, степень сухости пара и количество отданной им теплоты, если он охладился до 60 ℃.

Пользуясь справочной таблицей, получаем при t₂ = 60 ℃ давление пара

p = 0,019917 М П а

Так как процесс происходит при постоянном объеме, то

υ 1 = υ 2 = υ 1 ’ ’ = 0,1946 м 3 к г

Пользуясь таблицей, находим,

υ 2 ’ ’ = 7,678 м 3 к г

и таким образом

x 2 = 0,1946 7,678 = 0,0253

Количество теплоты в изохорном процессе

Определяем значения внутренней энергии пара в начале и в конце процесса:

u 1 = i 1 — p 1 υ 1 = 2778 — 1 × 10 3 × 0,1946 = 2583,4 к Д ж к г

i 2 = i 2 ’ + r x 2 = 251,2 + 2358,8 × 0,0258 = 310,8 к Д ж к г

u 2 = i 2 — p 2 υ 2 = 310,8 — 0,019917 × 10 3 × 0,1946 = 306,9 к Д ж к г

q υ = 306,9 — 2583,4 = — 2276,5 к Д ж к г

Так как в рассматриваемом процессе участвует 1 м 3 пара и плотность его по таблице при p = 1 МПа

ρ = 5,139 к г м 3

q υ ’ = ρ q υ = 5,139 × — 2276,5 = — 11699 к Д ж к г

Ответ: q’_υ = -11699 кДж/кг.

Задача #66310

1 кг пара расширяется адиабатно от начальных параметров p₁ = 3 МПа и t₁ = 300 ℃ до p₂ = 0,05 МПа.

По диаграмме is водяного пара находим для начального состояния (p₁ = 3 МПа и t₁ = 300 ℃):

i 1 = 2988 к Д ж к г

υ 1 = 0,08119 м 3 к г

Проведя на диаграмме is адиабату до пересечения с изобарой p₂ = 0,05 МПа, находим

i 2 = 2269 к Д ж к г

— конечный удельный объем

υ 2 = 2,76 м 3 к г

u 1 = i 1 — p 1 υ 1 = 2988 — 3 × 10 3 × 0,082 = 2744 к Д ж к г

u 2 = i 2 — p 2 υ 2 = 2269 — 0,05 × 10 3 × 2,76 = 2131 к Д ж к г

Работа пара в процессе

l = u 1 — u 2 = 2744 — 2131 = 613 к Д ж к г

Ответ: не указан.

Задача #66311

1 кг пара расширяется адиабатно от начальных параметров p₁ = 9 МПа и t₁ = 500 ℃ до p₂ = 0,004 МПа.

По диаграмме is и таблицам водяного пара находим:

i 1 = 3386 к Д ж к г

υ 1 = 0,0368 м 3 к г

Проведя в диаграмме is адиабату до пересечения с изобарой p = 0,004, получаем

i 2 = 2005 к Д ж к г

υ 2 = 27 м 3 к г

Внутренняя энергия пара:

u 1 = i 1 — p 1 υ 1 = 3386 — 9 × 10 3 × 0,0368 = 3054,8 к Д ж к г

u 2 = i 2 — p 2 υ 2 = 2005 — 0,004 × 10 3 × 27 = 1897 к Д ж к г

l = u 1 — u 2 = 3054,8 — 1897 = 1157,8 к Д ж к г

Ответ: не указан.

Задача #6632

В паровом котле находится 8250 кг пароводяной смеси с паросодержанием x = 0,0015 при давлении 0,4 МПа.

Сколько времени необходимо для поднятия давления до 1 МПа при закрытых вентилях, если пароводяной смеси сообщается 18 МДж/мин?

Удельный объем пароводяной смеси

υ x = υ 1 ’ ’ x 1 + 1 — x 1 υ 1 ’ = 0,4624 × 0,0015 + 0,9985 × 0,0010836 = 0,00177 м 3 к г

Конечное содержание пара

x 2 = υ x — υ 2 ’ υ 2 ’ ’ — υ 2 ’ = 0,00177 — 0,0011273 0,1946 — 0,0011273 = 0,00332

Так как изменение состояния пароводяной смеси происходит при постоянном объеме, то количество теплоты, необходимой для поднятия давления до 1 МПа, составит

Q υ = M i 2 — i 1 + p 1 υ — p 2 υ

Определяем энтальпию пара в начальном и конечном состояниях:

i 1 = i 1 ’ + r 1 x 1 = 604,7 + 2133 × 0,0015 = 607,9 к Д ж к г

i 2 = i 2 ’ + r 2 x 2 = 762,7 + 2 015 × 0,00 332 = 769,4 к Д ж к г

Q υ = 82 5 0 × 769,4 — 607,9 + 0,4 × 10 3 × 0,00177 — 1 × 10 3 × 0,00177 = 1328250 к Д ж

Время, необходимое для поднятия давления до 1 МПа при закрытых вентилях, составляет

τ = Q υ D = 1328250 18000 = 73,8 м и н .

Ответ: τ = 73,8 мин.

Задача #6633

Влажный пар имеет при давлении p = 1,5 МПа паросодержание x = 0,80.

Какое количество теплоты нужно сообщить 1 кг данного пара, чтобы довести его степень сухости при постоянном давлении до x₂ = 0,95.

Количество теплоты в изобарном процессе

Для рассматриваемого случая

q p = i ’ + r x 2 — i ’ + r x 1 = r x 2 — x 1 = 1947 × 0,95 — 0,8 = 292 к Д ж к г

Ответ: q_p = 292 кДж/кг.

Задача #6634

1 кг водяного пара при p = 1 МПа и t₁ = 240 ℃ нагревается, при постоянном давлении до 320 ℃.

Определить затраченное количество теплоты, работу расширения и изменение внутренней энергии пара.

Количество теплоты в изобарном процессе

Так как при p = 1 МПа температура насыщения

то пар заданных параметров перегретый. Пользуясь таблицами перегретого пара, получаем

q p = 3091 — 2918 = 173 к Д ж к г

l p = p υ 2 — υ 1

или, пользуясь таблице

l p = 1 × 10 3 × 0,2677 — 0,2274 = 40,3 к Д ж к г

Изменение внутренней энергии проще всего определится из уравнения первого закона термодинамики:

Δ u p = q p — l p = 173,0 — 40,3 = 132,7 к Д ж к г

Ответ: q_p = 173 кДж/кг; l_p = 40,3 кДж/кг; Δu_p = 132,7 кДж/кг.

Задача #6635

Энтальпия влажного насыщенного пара при давлении p₁ = 1,4 МПа составляет i_x = 2705 кДж/кг.

Как изменится степень сухости пара, если к 1 кг его будет подведено 40 кДж теплоты при постоянном давлении?

Определяем начальную степень сухости пара из равенства

i x 1 = i ’ + r x 1

Из таблиц водяного пара при p = 1,4 МПа:

i ’ = 830 к Д ж к г

r = 1960 к Д ж к г

x 1 = i x 1 — i 1 ’ r = 2705 — 830 1960 = 0,957

Конечную степень сухости пара определяем из равенства:

q p = i 2 — i 1 = i ’ + r x 2 — i ’ + r x 1 = r x 2 — x 1

из которого получаем

x 2 = q p r + x 1 = 40 1960 + 0,96 = 0,98

Задача #6636

Из парового котла поступает в пароперегреватель 2700 кг/ч пара при p = 1,6 МПа и x = 0,98. Температура пара после пароперегревателя равна 400 ℃.

Найти количество теплоты, которое пар получает в пароперегревателе, и отношение диаметров паропроводов до и после пароперегревателя, считая скорости пара в них одинаковыми.

Количество теплоты, которое нужно затратить для превращения 1 кг пара заданных начальных параметров в перегретый пар,

Пользуясь таблицами, находим

q p = 3253 — 858,3 + 1935 × 0,98 = 498,4 к Д ж к г

Общее количество теплоты

Q p = M q p = 2700 × 498,4 = 1345680 к Д ж ч

Определяем значения удельного объема пара до и после пароперегревателя:

υ 1 = υ 1 ’ ’ x 1 = 0,1238 × 0,98 = 0,121 м 3 к г

Пользуясь таблицей, получаем

υ 2 = 0,1899 м 3 к г

Обозначая сечения трубопровода до и после пароперегревателя соответственно через F₁ и F₂ и скорость протекания пара в них через w, получаем

F 1 w υ 1 = F 2 w υ 2

F 1 F 2 = υ 1 υ 2

d 1 d 2 = υ 1 υ 2 = 0,1210 0,1937 = 0,798

Задача #6637

2 кг пара, занимающие при р = 0,8 МПа объем V₁ = 0,15 м 3 , изотермически расширяются до V₂ = 0,35 м 3 .

Определить работу расширения, количество подведенной теплоты и степень сухости пара.

Определяем удельный объем пара:

υ 1 = V 1 M = 0,15 2 = 0,075 м 3 к г

υ 2 = V 2 M = 0,35 2 = 0,175 м 3 к г

При p₁ = 0,8 МПа удельный объем сухого насыщенного пара

υ ’ ’ = 0,2403 м 3 к г

Так как υ₁ и υ₂ меньше υ’’, то пар в начальном и конечном состояниях влажный.

x 1 = υ 1 — υ ’ υ ’ ’ — υ ’ = 0,075 — 0,001 0,2403 — 0,001 = 0,309

x 2 = υ 2 — υ ’ υ ’ ’ — υ ’ = 0,175 — 0,001 0,2403 — 0,001 = 0,727

Работа расширения и количество подведенной теплоты могут быть определены по формулам изобарного процесса, так как рассматриваемый изотермический процесс, протекающий в области влажного пара, одновременно является процессом изобарным. Следовательно, работа расширения определяется по уравнению:

L = M p V 2 — V 1 = 2 × 0,8 × 10 6 × 0,35 — 0,15 = 320000 Д ж = 320 к Д ж

Q = M r x 2 — x 1 = 2 × 2048 × 0,727 — 0,309 = 1712 к Д ж

Ответ: L = 320 кДж; Q = 1712 кДж; x₁ = 0,309; x₂ = 0,727.

Задача #6638

1 кг пара при давлении p₁ = 0,6 МПа и температуре t₁ = 200 ℃ сжимают изотермически до конечного объема υ₂ = 0,11 м 3 /кг.

Определить конечные параметры и количество теплоты, участвующей в процессе.

Начальной температуре t₁ = 200 ℃ соответствует давление насыщения

p = 1,5551 М П а > p 1 = 0,6 М П а

поэтому пар в начальном состоянии перегретый.

Кроме того, при температуре 200 ℃

υ ’ ’ = 0,1272 м 3 к г

υ 2 = 0,11 м 3 к г υ ’ ’ = 0,1272 м 3 к г

т. е. пар в конечном состоянии влажный насыщенный, а так как его температура равна начальной, то соответствующее ей давление

p 2 = 1,5551 М П а

Степень сухости пара найдем из уравнения:

x = υ x υ ’ ’ = 0,11 0,1272 = 0,86

Количество теплоты определим по формуле:

Значения энтропии s₁ и s₂ находим по диаграмме is:

s 1 = 6,963 к Д ж к г × К

s 2 = 5,8576 к Д ж к г × К

q = 473 × 5,8576 — 6,963 = — 522,9 к Д ж к г

Ответ: не указан.

Задача #6639

Сухой насыщенный водяной пар расширяется адиабатно от давления 1 МПа до 0,05 МПа.

Определить степень сухости в конце расширения. Задачу решить при помощи диаграммы is и аналитическим путем.

1) На диаграмме is находим точку пересечения изобары p = 1 МПа с верхней пограничной кривой. Из этой точки проводим адиабату (опускаем вертикаль) до пересечения с изобарой р = 0,05 МПа. Полученная точка определяет степень сухости в конце адиабатного расширения:

2) Так как в адиабатном процессе s₁ = s₂, то

s 1 ’ ’ = s 2 ’ + r 2 x 2 T н 2

x 2 = s 1 ’ ’ — s 2 ’ r 2 T н 2 = s 1 ’ ’ — s 2 ’ s 2 ’ ’ — s 2 ’ = 6,587 — 1,091 7,593 — 1,091 = 0,845

Задача #6641

Определить абсолютную влажность воздуха, если парциальное давление пара в нем p_п = 0,014 МПа, а температура t = 60 ℃. Барометрическое давление равно 101325 Па (760 мм рт. ст.).

Температуре t = 60 ℃ по справочной таблице соответствует давление

p н = 0,019917 М П а

Следовательно, при парциальном давлении p_п = 0,014 МПа пар перегрет.

По таблице для p = 0,014 МПа и t = 60 ℃ имеем

υ = 10,95 м 3 к г

Следовательно, абсолютная влажность

ρ п = 1 υ = 1 10,95 = 0,0913 к г м 3

Ответ: ρп = 0,0913 кг/м 3 .

Задача #6642

Определить влагосодержание воздуха при температуре t = 60 ℃ и барометрическом давлении B = 99325 Па (745 мм рт. ст.), если относительная влажность воздуха φ = 60 %.

По таблице насыщенного водяного пара для температуры t = 60 ℃

p н = 0,019917 М П а

Парциальное давление пара

p п = φ p н = 0,6 × 0,019917 = 0,012 М П а

d = 622 p п B — p п = 622 × 0,012 0,099325 — 0,012 = 85,5 г к г

Ответ: d = 85,5 г/кг.

Задача #6643

Каково состояние воздуха, если температура его равна 50 ℃, а парциальное давление пара в нем p_п = 8000 Па (60 мм рт. ст.).

При температуре t = 50 ℃ давление насыщения

p н = 0,12335 М П а

p п = 8000 П а p н = 12335 П а

то пар воздуха перегрет, а следовательно, воздух при этом не насыщен.

Ответ: воздух не насыщен.

Задача #6644

Парциальное давление пара в атмосферном воздухе составляет 0,02 МПа, температура воздуха равна 70 ℃. Определить относительную влажность воздуха.

Температуре 70 ℃ соответствует давление

p н = 0,03117 М П а

Следовательно, при парциальном давлении 0,02 МПа пар перегрет.

Из таблицы перегретого пара для p = 0,02 МПа и t = 70 ℃ получаем

υ = 7,037 м 3 к г

ρ п = 1 υ = 1 7,037 = 0,127 к г м 3

Из таблицы насыщенного паря для t = 70 ℃

ρ н = ρ ’ ’ = 0,1982 к г м 3

отсюда относительная влажность воздуха

φ = ρ п ρ н 100 = 0,127 0,1982 × 100 = 64,1 %

Тот же результат получится, если из таблицы найти давление насыщения при температуре t = 70 ℃:

p н = 0,03117 М П а

φ = p п p н 100 = 0,02 0,03117 × 100 = 64,2 %

Задача #6645

Наружный воздух, имеющий температуру t = 20 ℃ и влагосодержание d = 6 г/кг, подогревается до температуры 45 ℃.

Определить относительную влажность наружного и подогретого воздуха. Барометрическое давление принять равным 0,1 МПа.

Относительную влажность воздуха находим по формуле:

Величина p_н определяется по таблицам насыщенного пара и при температуре t = 20 ℃ составляет

p н = 0,002337 М П а

Парциальное давление водяного пара в воздухе при данном барометрическом давлении является функцией .только влагосодержания и определяется по формуле:

p п = p d 622 + d = 0,1 × 6 622 + 6 = 0,00096 М П а

φ 1 = 0,00096 × 100 0,002337 = 41 %

В процессе подогрева влагосодержание воздуха не изменяется. Следовательно, остается неизменным и парциальное давление пара. Давление насыщения p_н при температуре t = 45 ℃ составит

Источник