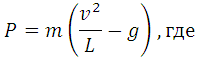Если достаточно быстро вращать ведро с водой

Если достаточно быстро вращать

27958. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю.

В верхней точке сила давления, выраженная в ньютонах, равна

m — масса воды в килограммах,

v — скорость движения ведeрка в м/с,

L — длина верeвки в метрах,

g — ускорение свободного падения (считайте g = 10 м/с 2 ).

С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верёвки равна 40 см? Ответ выразите в м/с.

Понятно, что чем выше скорость вращения, тем больше давление воды (в том числе и в верхней точке). Нам необходимо найти минимальную скорость, при которой вода не будет выливаться, то есть скорость, при которой давление в верхней точке будет равным нулю (вода как бы зависнет) Р = 0. Решаем уравнение, сантиметры переводим в метры (40см = 0,4м):

Произведение равно нулю, когда один из множителей равен нулю, m≠ 0 (это масса воды), значит

При скорости вращения 2 м/с вода выливаться не будет. Если же скорость будет от 0 до 2 м/с давление в верхней точке будет отрицательным и вода выльется.

Источник

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Источник

Весёлый эксперимент с крутящимся ведром

Что такое центростремительная сила и можно ли перевернуть ведро с водой над собой и не быть облитым с ног до головы?

Вы всегда думали, что если перевернуть ведро с водой над головой промокните до ниточки? Тогда этот эксперимент вам точно подойдёт. С его помощью можно не только отлично повеселиться, но и показать ребёнку особенности такого природного явления, как центростремительная сила.

Вам понадобятся:

1) Небольшое пластиковое или металическое ведро до 5 литров с крепкой ручкой. Очень важно, чтобы во время эксперимента она не оторвалась;

2) Прозрачная вода. Можно даже набрать тёплую, чтобы было не так неприятно, в случае если эксперимент с первого раза не удастся;

3) Длинная и крепкая верёвка, которая сможет выдержать вес вращающегося ведра.

Порядок действий:

1. Эксперимент стоит проводить на открытом пространстве. Очень не рекомендуется пробовать сделать опыт внутри дома ведь вода может разлиться и повредить мебель.

2. Крепко привяжите длинную верёвку к ручке ведра.

3. Наполните ведро водой на половину.

4. Возьмите конец верёвки в вытянутую руку и начинайте раскручивать ведро движениями влево и вправо пока не начнете крутить ведро по кругу. Старайтесь делать это быстро, так чтобы вся вода сохранялась внутри ведра. Будьте готовы к тому, что если скорость кручения будет недостаточно высока, вы разольёте всю воду на себя.

5. Когда рука устанет крутить, аккуратно в начале спуска после пиковой точки сбавьте скорость ведра и плавно остановите его так, чтобы вода не расплескалась.

Что происходит?

Всем телам свойственна инерция (с латинского бездеятельность) или, другими словами, явление сохранения скорости. Это значит, что когда вы раскручиваете ведро и оно оказывается в верхней точке, в которой вода должна была бы вылиться на вас, кроме силы притяжения действует сила сохранения скорости. Именно поэтому вода не выливается и остаётся в ведре, до тех пор, пока вы будете крутить верёвку с достаточной скоростью. Это и называется центростремительная сила, то есть такая, которая действует на объект движущийся по круговой траектории и направлена к её центру. Поэтому, до тех пор пока вы будете крутить ведро с достаточной скоростью ни одна капля воды не выльется из него.

Как ещё поэкспериментировать?

Возьмите простой стакан наполненный водой в одну руку и быстро двигайте его в сторону. Другой рукой резко остановите движение стакана. Часть воды из него выплеснется. Это ещё один отличный пример инерции. Вода продолжает двигаться с заданной скоростью даже после остановки стакана и поэтому выплёскивается наружу.

Факты

1. Основы нашего эксперимента с ведром описал в своём первом законе Ньютон: свободное тело, на которое не действуют силы со стороны других тел, находится в состоянии покоя или прямолинейного движения.

2. Эффект инерции и центростремительной силы используют на аттракционах и спутниках, которые находятся на околоземной орбите.

3. В быту можно увидеть пример инерции и центростремительной силы просто сбивая резкими встрясками показания ртутного термометра перед использованием.

Источник

10. Прикладные задачи

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

Линейные, квадратные, кубические уравнения и неравенства

При температуре $0^ <\circ>C$ рельс имеет длину $l_0 = 10$ м При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $l(t^<\circ>) = l_0 (1+\alpha t^<\circ>)$ , где $a = 1,2 \cdot 10^ <-5>(^<\circ>C)^<-1>$ — коэффициент теплового расширения, $t^<\circ>$ — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.

Компания продает свою продукцию по цене p = 500 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v = 300 руб., постоянные расходы предприятия f = 700 000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле $\pi (q) = q\cdot (p-v) — f$. Определите наименьший месячный объем производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300 000 руб.

Если достаточно быстро вращать ведерко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна $P = m \big( \frac — g \big)$, где m – масса воды в килограммах, v – скорость движения ведерка в м/с, L – длина веревки в метрах, g – ускорение свободного падения (считайте $g = 10 \text<м/>c^2$). С какой наименьшей скоростью надо вращать ведерко, чтобы вода не выливалась, если длина веревки равна 40 см? Ответ выразите в м/с.

Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой $y = ax^2 + bx$, где $a = -\frac<1> <100>\text<м>^<-1>$, $b = 1$ – постоянные параметры x (м) – смещение камня по горизонтали y (м) – высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?

Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением закону $T(t) = T_0 + bt +at^2$, где t – время в минутах, $T_0 = 1400K, \; a = -10K / \text<мин>^2, \; b = 200 K/ \text<мин>$.

Известно, что при температуре нагревателя свыше 1760 K прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.

Автомобиль, движущийся в начальный момент времени со скоростью $v_0 = 20 \text <м>/ c$ начал торможение с постоянным ускорением $a = 5 \text <м>/ c^2$. За t секунд после начала торможения он прошёл путь $S = v_0t — \frac<2>$ (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных соосных цилиндров: центрального массой $m = 8$ кг, радиуса $R = 10$ см и двух боковых с массами $M = 1$ кг и с радиусами $R + h$. При этом момент инерции катушки относительно оси вращения, выражаемый в кг $\cdot \text<см>^2$ , даётся формулой: $I = \frac<(m +2M)R^2> <2>+ M(2Rh + h^2)$.

При каком максимальном значении h момент инерции катушки не превышает предельного значения $625$ кг $\cdot \text<см>^2$? Ответ выразите в сантиметрах.

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием $f = 30 $ см. Расстояние $d_1$ от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние $d_2$ от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение $\frac<1> + \frac<1> = \frac<1>$. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было четким. Ответ выразите в сантиметрах.

Перед отправкой тепловоз издал гудок с частотой $f_0 = 440 $ Гц . Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону $f(v) = \frac<1-\frac>$ (Гц), где c – скорость в звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а $c = 315 \text<м/с>$. Ответ выразите в м/с.

В розетку электросети подключены приборы, общее сопротивление которых составляет $R_1 = 90$ Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление $R_2$ этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями $R_1$ Ом и $R_2$ Ом их общее сопротивление дается формулой $R_<\text<общ>> = \frac$ (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.

Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой $m_<\text<в>>$ (в килограммах) от температуры $t_1$ до температуры $t_2$ (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы $m_<др>$ (кг) кг. Он определяется формулой $\eta = \frac> \cdot m_<\text<в>> (t_2 — t_1)>> \cdot m_<\text<др>>> \cdot 100\% $, где $c_<\text<в>> = 4,2 \cdot 10^3 (\frac<\text<Дж>> <кг>\cdot K)$ – теплоёмкость воды $q_<\text<др>> = 8,3 \cdot 10^6 $ Дж/кг – удельная теплота сгорания дров.

Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть $m_<\text<в>> = 83$ кг воды от 10°C до кипения, если известно, что КПД кормозапарника не больше 21%. Ответ в килограммах.

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле:

$v = c\frac, \; \text <где>\; c = 1500 \text<м/с>$ – скорость звука в воде, $f_0$ – частота испускаемых импульсов (в МГц), $f$ – частота отраженного от дна сигнала, регистрируемая приёмником (в МГц).

Определите наибольшую возможную частоту отраженного сигнала $f$, если скорость погружения батискафа не должна превышать 2 м/с.

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t 2 , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. Насколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.

Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задается формулой q = 100 – 10p. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r (p) = q ∙ p. Определите наибольшую цену p, при которой месячная выручка r (p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.

В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём выраженная в метрах, меняется по закону H (t) = at 2 + bt + H₀, где H₀ = 4 м — начальный уровень воды, а = $\frac<1><100>$ м/мин 2 и b = –$\frac<2><5>$ м/мин 2 ― постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.

Для сматывания кабеля на заводе используют лебедку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону φ = ωt + $\frac<\beta t^2><2>$, где t ― время в минутах, ω = 20°/мин ― начальная угловая скорость вращения катушки, β = 4°/мин ― угловое ускорение, с которым наматывается кабель.

Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки φ достигнет 1200°. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.

По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I = $\frac<\varepsilon>$, где ɛ

— ЭДС источника (в вольтах), r = 1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания I_кз = $\frac<\varepsilon>$? (Ответ выразите в Омах).

Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле A_ω = $\frac<|\omega_p^2 - \omega^2|>$, где w ― частота вынуждающей силы ( в с -1 ), А₀ ― постоянный параметр, ω_p = 360 c -1 ― резонансная частота. Найдите максимальную частоту w, меньшую резонансной, для которой амплитуда колебаний превосходит величину A₀ не более чем на 12,5%. Ответ выразите в c -1 .

Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой η = $\frac$ ∙ 100%, где T₁ — температура нагревателя (в градусах Кельвина), T₂ — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T₁ КПД этого двигателя будет не меньше 15%, если температура холодильника Т₂ = 340К? Ответ выразите в градусах Кельвина.

При сближении источника и приёмника звуковых сигналов движущихся в некоторой среде по прямой навстречу друг другу частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала f₀ = 150 Гц и определяется следующим выражением: f = f₀ $\frac$(Гц), где c — скорость распространения сигнала в среде (в м/с), u = 10 м/с и ʋ = 15 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 160 Гц.

Автомобиль, масса которого равна m = 2160 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S = 500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно F = $\frac<2ms>$. Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400Н. Ответ в секундах.

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая сила, выражаемая в ньютонах, будет определяться по формуле:

Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: F_a = αpgr 3 , где α = 4,2 ― постоянная, r ― радиус аппарата в метрах, p = 1000 кг/м 3 ― плотность воды, g ― ускорение свободного падения (считайте g = 10 H/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ запишите в метрах.

Источник