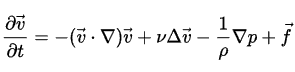Физика перемещение по воде

Основные законы движения жидкостей и газов

Для расчета движения воды в трубопроводе нужно знать не так уж и много. Для этого не надо глубоко изучать физику, но всё же некоторое основные понятия изучить придется.

В этой статье я приведу самые основные формулы, которые вам пригодятся не только для расчетов, но и для общего понимания, что может влиять в вашем водопроводе на его течение. Иногда общее понимание процессов поможет вам избежать ошибок при монтаже системы.

Например, не все знают, что в части водопровода с трубами меньшего диаметра давление на стенки меньше, чем на участке с трубами большего диаметра. Почему возникает кавитация и вообще, что это такое. А это надо знать.

Статья будет обновляться и дополняться.

Уравнение неразрывности

Для жидкости, текущей в трубе, этот закон используют в такой форме (называемой уравнением неразрывности):

Где v — скорость жидкости S — площадь сечения трубы, по которой течёт жидкость. Сформулировать этот закон можно и так:

Сколько вливается жидкости в ёмкость, в данном случае в трубу, столько должно и выливаться, если условия течения не изменяются.

Скорость в узких участках трубы должна быть выше, чем в широких.

Уравнение Бернулли стационарного движения

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 — 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.

Идеальная жидкость — жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.

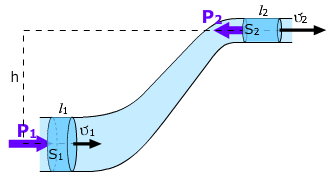
Уравнение стационарного движения, носящее его имя, имеет вид:

P +	ρ⋅v²	+ ρ⋅g⋅h = const
	2

где P — давление жидкости, ρ − её плотность, v — скорость движения, g — ускорение свободного падения, h — высота, на которой находится элемент жидкости.

Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.

В уравнении Бернулли есть три слагаемых:

• ρ⋅v 2 /2 — динамическое давление — кинетическая энергия единицы объёма движущей жидкости;
• ρ⋅g⋅h — весовое давление — потенциальная энергия единицы объёма жидкости;
• P — статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

Явление кавитации

Кавитация (от латинского cavitas — «углубление», «полость») — процесс образования полостей (пузырьков) в движущейся жидкости вследствие понижения давления.

Явление кавитации также объясняется уравнением Бернулли. Если скорость течения жидкости значительно возрастает, то давление сильно понизится — настолько, что жидкость закипит. Такую скорость можно получить, если пропускать жидкость через очень узкий участок трубы или при быстром обращении лопатки в водяном насосе.

Пузырьки по ходу движения жидкости попадают в области жидкости с нормальным давлением и там схлопываются. Это схлопывание сопровождается гидродинамическими эффектами, способными привести к разрушению трубы или стенок насоса.

Гидродинамика Эйлера и Навье-Стокса

Уравнение Бернулли позволяет объяснить очень много интересных гидродинамических явлений, но гораздо больше явлений, происходящих в движущихся жидкостях и газах, с его помощью объяснить нельзя, потому что этот закон для идеальной жидкости, т.е для жидкости, которая не обладает внутренним трением, а значит не создает гидравлическое сопротивление..

Реальная жидкость отличается от идеальной и обладает внутренним трением, или по другому называют вязкостью. Два соприкасающиеся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый.

Закон вязкого трения Ньютона

Ньютон предположил, что величина этой силы (называемой силой внутреннего трения) пропорциональна разности скоростей элементов жидкости. Следовательно, сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости:

F =	η⋅S⋅	dv
		dy

η − коэффициент динамической вязкости.

Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются ньютоновскими, или жидкостями с линейной вязкостью.

Величину коэффициента динамической вязкости (и справедливость данного закона) Ньютон определил с помощью несложного опыта: он передвигал по поверхности жидкости пластинку с той или иной скоростью. Для того чтобы поддерживать эту скорость постоянной, требовалась сила, которая при небольшой глубине жидкости оказалась прямо пропорциональна площади S и скорости пластинки v и обратно пропорциональна глубине жидкости h:

F =	η⋅S⋅v
	h

И хотя при увеличении глубины жидкости h сила вязкого трения пластинки не становится исчезающе малой, эта формула довольно точно описывает взаимодействие между соприкасающимися элементами жидкости.

Чем больше разность скоростей, тем больше сила, с которой они воздействуют друг на друга, заставляя притормаживать слишком быстро движущиеся элементы и разгоняя слишком медленные.

В результате относительное движение в жидкости прекращается (но иногда это может произойти не очень скоро).

Уравнение Навье — Стокса для вязких жидкостей

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье — Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье — Стокса и закон Ньютона совпадают).

Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье — Стокса, т.е. являются ньютоновскими жидкостями.

Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера — это частный (предельный) случай больших скоростей гидродинамики Навье — Стокса.

При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).

Критерий Рейнольдса

Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 — 1912).

Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.

Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:

Eкин =	ρ⋅n³⋅	v²
		2

Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:

F =	η⋅v⋅n²	= η⋅v⋅n
	n

Работа этой силы при перемещении элемента жидкости на расстояние n составляет

а отношение кинетической энергии элемента жидкости к работе силы трения равно

Eкин	=	ρ⋅n³⋅v²
A		2⋅ η⋅v⋅n²

Сокращаем и получаем:

Re =	ρ⋅n⋅v
	2η

Re — называется числом Рейнольдса.

Таким образом, Re — это безразмерная величина, которая характеризует относительную роль сил вязкости.

Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.

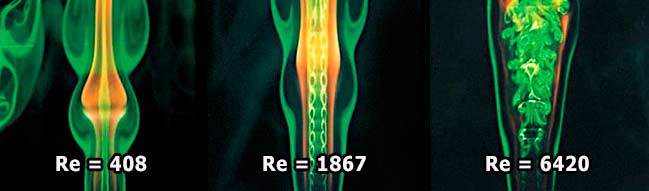
Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina — «пластинка») течение превращается в турбулентное (от латинского turbulentus — «бурный», «беспорядочный»), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.

Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен — охлаждение или нагревание агрегатов — происходит существенно интенсивнее; быстрее идёт распространение химических реакций.

Формула Бернулли закон по которому течет жидкость на любом отрезке трубы, что значительно помогает при проектировании трубопроводов, особенно с естественной циркуляцией.

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Источник

Физики научились перемещать объекты по воде при помощи волн

Ученые из Австралии, Израиля и России научились с помощью волны перемещать объекты на поверхности воды. Результаты своего исследования авторы опубликовали в журнале Nature Physics, а кратко с ними можно ознакомиться на сайте Австралийского национального университета в Канберре.

Фото: Stuart Hay

Специалисты с помощью волновых генераторов заставили объекты, находящиеся на поверхности воды, двигаться в направлении, противоположном направлению распространения волны, то есть к ее источнику.

Волны определенной частоты физики создавали при помощи вертикальных колебаний клапанов, расположенных на воде. По словам ученых, такие колебания создавали у поверхности жидкости специальные трехмерные волны и вихри, геометрия и динамика которых в целом определяли направление, а также скорость движения объектов.

Ученые в своих экспериментах изучали движение шарика для пинг-понга. Для опытных бассейна и шарика физикам удалось определить набор волновых частот, необходимых для перемещения объекта в любых направлениях.

Исследование носит только экспериментальный характер. Последовательной математической теории, которая бы объясняла наблюдаемые эффекты по перемещению объектов по поверхности воды, пока нет.

Ученые считают, что их открытие может найти применение при устранении последствий разливов нефти и масел в морях, а также окажется полезным для дистанционного манипулирования объектами на воде.

Источник

Физика в мире животных: как водомерки бегают по воде

Среди читателей Хабра, вероятно, нет людей, которые никогда не видели водомерок. Это очень распространенное семейство насекомых, которое включает около 1700 видов. Большинство — пресноводные, но есть и виды, которые живут на побережье морей и океанов.

Всю свою жизнь водомерки проводят на поверхности воды. Они передвигаются по ней так же просто, как обычные насекомые — по суше. Водомерки, по крайней мере, большинство видов — хищники. Они питаются мелкими организмами, но не боятся нападать и на более крупную добычу. Иногда ничего не подозревающий малек подплывает к поверхности водоема, и тут же в него всаживается «гарпун» — хоботок водомерки, которая впрыскивает в тело жертвы желудочный сок и начинает всасывать питательные вещества. В общем, неплохой сюжет для нескучного фильма. Но самое интересное в водомерке — ее способность бегать по воде. Каким образом это насекомое получило свою сверхспособность?

Физика и химия — друзья водомерок

В большинстве случаев водомерки держатся на воде благодаря, во-первых, наличию слоя водоотталкивающих жиров на тельце и конечностях, во-вторых, благодаря специальным волоскам на кончиках лапок.

Так, на задних лапках насекомых этих волосков очень много, их количество превышает 16 000 на мм 2 . На них водомерки опираются, они же служат рулевым механизмом. На средних и передних конечностях волосков тоже много, но не настолько. Волоски водомеркам приходится довольно часто приводить в порядок, поскольку если этого не делать, вода смочит тело водомерки и та утонет.

Предназначение волосков — создать воздушную подушку, на которой и покоится водомерка. Если присмотреться в солнечный день, то можно видеть, как сверкает вода вокруг лапок водомерки — это как раз воздушный «кокон» или, если угодно, воздушная подушка. На дне неглубокого водоема видна тень водомерки — и всегда вокруг лапок тень утолщена, хотя сами лапки вполне обычные — это тень от создаваемой волосками конечностей воздушной подушки.

Кстати, китайские ученые обнаружили интересный факт — время от времени тень от ножки перестает быть четкой, и тогда водомерка прижимает ее к передней части тела, где находятся железы, выделяющие несмачиваемое вещество. После этой процедуры тень от конечности снова становится четкой.

Волоски у водомерок тоже необычные, вдоль каждого из них проходит желобок, что предотвращает проникновение воды — она не может просочиться в столь малый объем. Угол соприкосновения воды с поверхностью конечностей водомерки составляет около 168 градусов, что предотвращает смачивание лапок.

Некоторые виды водомерок передвигаются и при помощи «химического двигателя». В задней части тела насекомых есть специализированная железа, которая выделяет жироподобное вещество. Оно изменяет силу поверхностного натяжения, снижая ее. В результате водомерка движется вперед уже благодаря действию уже законов физики. Водомерка скользит в создаваемой ею водной «лунке». Когда нужно выйти на берег, то выделение гидрофобного вещества снижается, и водомерка выбирается при помощи капиллярных сил.

Режим передвижения водомерок

Насекомые эти получили свое русское название из-за того, что передвигаясь, они как бы «меряют» пройденное по воде расстояние. Но, как оказалось, это лишь один режим передвижения водомерки — так она поступает, когда не испугана и не преследует жертву, а просто передвигается по поверхности воды.

Большинство видов попеременно опираются на три конечности, перемещая остальные три вперед, и повторяя этот цикл.

В моменты опасности или преследования добычи водомерка как бы втыкает в поверхность воды кончики средних лап, на которых не так много волосков, рулит задними, а передними — загребает воду. Единственное — передние лапки все же не погружаются в воду, а отталкиваются от поверхности воды.

Ну и последнее — водомерки умеют прыгать на воде. Не очень далеко, но это все же прыжки. Прыгают они в случае опасности — за этим можно наблюдать, если попробовать накрыть водомерку ладонью на воде. Спасаясь, она будет не только «грести», но и прыгать, причем довольно активно.

К слову, если изменить поверхностное натяжение воды — например, при помощи поверхностно-активных веществ (ПАВ), то водомерки потонут. Именно поэтому их нет в местах сброса в воду отходов производства — последние изменяют свойства воды и водомерки (да и не только они) не могут жить в подобных местах.

Водомерки приносят пользу науке

Группа китайских ученых разработала сверхточный метод измерения силы Архимеда. Идея пришла в голову сначала одному китайскому физику по имени Юй Тянь (Yu Tian) из университета Цинхуа в Пекине

Ученый в солнечный день отправился к берегу пруда в одном из парков столицы Китая. Там он смотрел на воду и заметил водомерок, которые отбрасывали тень. Как и говорилось выше, тень от их лапок была отличной от конфигурации кончиков конечностей.

Ученый понял, что это вызвано искривлением воды под действием веса водомерки, сколь бы небольшим он ни был. И тогда он понял, что при помощи теней, отбрасываемых объектами на поверхности воды, можно измерять силу Архимеда, причем эти измерения сверхточные. Граница чувствительности метода — 1 пиконьютон.

«Геометрия тени, которую отбрасывает на воду объект, позволяет очень точно вычислить искривление поверхности воды под ним, и, соответственно, определить объем этой „лунки“ и вычислить силу выталкивания, используя закон Архимеда. Все это можно измерить, используя фонарик, прозрачный сосуд, воду и простую камеру», — заявил ученый.

Еще и роботы

Результаты наблюдения китайского ученого помогли его команде разработать концепцию робота-водомерки. На данный момент таких устройств создано несколько, причем одно из них умеет даже прыгать по поверхности воды, как настоящая водомерка.

Первыми создателями робота-водомерки была команда School of Chemical Engineering and Technology. Разработчики использовали как результаты наблюдений коллег, так и собственные исследования.

Затем был создан еще один робот, вес которого составлял много больше, чем у водомерки — 11 граммов вместо долей грамма. Он способен передвигаться по воде и делает это довольно быстро — вплоть до 5 км/ч, что сравнимо со скоростью ходьбы взрослого человека.

Ну и еще один показательный пример — робот-водомерка, созданный объединенной командой исследователей из Южной Кореи и США. Этот робот очень сильно напоминает водомерку, размер его составляет около 7 см вместе с «лапками».

Он не только передвигается по поверхности воды, но еще и прыгает, причем довольно высоко.

Область применения роботов-водомерок — поисково-спасательные операции, изучение физико-химических свойств воды, мониторинг загрязнений и т.п.

Источник