Как определить давление сосуда с водой

Как определить давление сосуда с водой

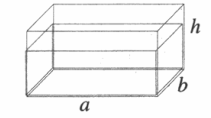
1. Вывод формулы для расчета давления жидкости на дно сосуда

Сила давления жидкости на дно сосуда равна весу этой жидкости: Fд = Р
Вес жидкости определяем по ее массе: Р = mg
Массу вычисляем по плотности (p) жидкости: m = pV
где объем жидкости равен занятому жидкостью объему прямоугольного сосуда: V = Sh

Тогда давление жидкости на дно и стенки сосуда:

2. От каких величин и как зависит давление жидкости на дно сосуда?

Давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.

3. Что можно рассчитать по этой формуле?

— давление жидкости на дно сосуда любой формы,
— давление жидкости на стенки сосуда на нужной высоте,
— давление внутри жидкости в любой точке во всех направлениях.

4. В каких единицах выражаются величины, входящие в формулу?

Входящие в формулу величины выражаются:
— плотность в кг/м 3 ,
— высота столба жидкости в метрах,
— g = 9,8 Н/кг,
— давление в Паскалях (Па).

5. Пример решения задачи

Задача.
Определить давление воды на дно бака, если высота столба воды в баке равна 3 м, а плотность воды — 1000 кг/м 3 .

Источник

Все, что необходимо знать о силе давления воды

Пловец, нырнувший глубоко, ощущает боль в ушах. На барабанные перепонки воздействует сила давления воды.

Корабль в воде не тонет благодаря выталкивающей силе. Вода способна легко изменять свою форму, она воздействует на поверхности тел при соприкосновении с ними.

Чему равна сила давления воды и что это такое, расскажем в статье.

Что это такое?

В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.

Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.

Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.

Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.

Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.

Факторы, влияющие на показатель

При отсутствии внешнего воздействия, играют роль два фактора:

Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.

Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:

При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?

Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.

Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.

Единицы измерения

Давление воды измеряют в:

• паскалях – Па;
• метрах водяного столба – м. в. ст.
• атмосферах – атм.

Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).

Формулы расчета

Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).

Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.

Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.

Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.

Расчет давления воды на дно и стенки сосуда в видео:

Применение на практике

Примеры использования знаний свойств воды:

1. Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
2. Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
3. Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
4. Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.

Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:

• выжимка масла из семян растений;
• спуск на воду со стапелей построенного судна;
• ковка и штамповка деталей;
• домкраты для подъема грузов.

Заключение

Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.

Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.

Источник

Статика. Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление).

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то дав­ление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидроста­тическим.

Получим формулу для расчета гидростатического давления жидкости на произвольной глубине h (в окрестности точки A на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления p в основании этого столба на площадь его сечения S:

2) как вес того же столба жидкости, т. е. произведение массы m жидкости на ускорение сво­бодного падения:

Масса жидкости может быть выражена через ее плотность p и объем V:

а объем — через высоту столба и площадь его поперечного сечения:

Подставляя в формулу (1.28) значение массы из (1.29) и объема из (1.30), получим:

Приравнивая выражения (1.27) и (1.31) для силы давления, получим:

Разделив обе части последнего равенства на площадь S, найдем давление жидкости на глубине h:

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободно­го падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе, давление на стенки сосуда, а так­же давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

Гидростатический парадокс .

Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

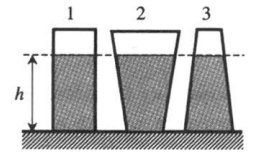
Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужа­ющихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: p = pgh (формула гидростатического давления жидкости). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосу­дов, одна и та же. Она равна весу вертикального столба ABCD жидкости: P = oghS, здесь S — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способ­ностью жидкости передавать давление одинаково во всех направлениях.

Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное дав­ление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давле­ние. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, подняв­шись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давле­ние в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Источник

Давление в жидкостях и газах. Закон Паскаля.

теория по физике 🧲 гидростатика

Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.

Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.

Давление столба жидкости определяется формулой:

p — давление столба жидкости (Па), ρ_ж— плотность жидкости (кг/м 3 ), g — ускорение свободного падения (≈10 м/с 2 ), h — высота столба жидкости, или ее глубина (м).

Важно! Высоту h нужно определять от поверхности жидкости.

Сила давления жидкости

Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:

Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:

F = ρ ж g h 2 . . h b

Подсказки к задачам:

• Плотность пресной воды равна 1000 кг/м 3 .
• Плотность соленой воды равна 1030 кг/м 3 .

Пример №1. Чему равно давление, созданное водой, на глубине 2 м?

Давление в жидкостях определяется формулой:

Давление, созданное пресной водой, равно:

p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)

Давление, созданное соленой водой, равно:

p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)

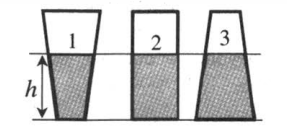
Гидростатический парадокс

Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.

Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:

F₁ 3 ), во втором — керосин (ρ₂ = 0,8 г/см 3 ), в третьем — спирт (ρ₃ = 0,8 г/см 3 ). В каком сосуде оказывается максимальное давление на дно?

Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.

В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м 2 ? Атмосферное давление не учитывать.

Алгоритм решения

1. Записать исходные данные и перевести единицы измерения величин в СИ.
2. Записать формулу для вычисления силы давления.
3. Выполнить решение задачи в общем виде.
4. Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Высота сосуда H = 20 см.
• Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
• Площадь дна сосуда: S = 0,01 м 2 .

Сила давления равна произведению давления на площадь, на которую это давление оказывается:

Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:

F = pS = ρ_жghS = ρ_жg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные и перевести единицы измерения величин в СИ.
2. Записать формулу для вычисления силы давления.
3. Выполнить решение задачи в общем виде.
4. Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Глубина заплаты в цистерне h = 2 м.
• Площадь заплаты: S = 10 см 2 .

10 см 2 = 0,001 м 2

Сила давления равна произведению давления на площадь, на которую это давление оказывается:

Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:

F = pS = ρ_кghS = 800∙10∙2∙0,001 = 16 (Н)

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.

Выберите два верных утверждения, согласующихся с приведёнными графиками.

а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.

б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.

в) Плотность керосина 0,82 г/см 3 , аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.

г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.

д) Плотность оливкового масла 0,92 г/см 3 , аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).

Алгоритм решения

Решение

Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.

Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.

Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.

Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.

Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.

Верный ответ: бд.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Читайте также:  Парфюмерная вода yves saint laurent sleek suede