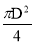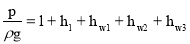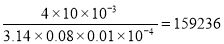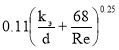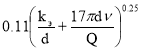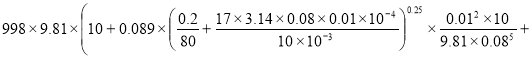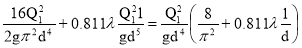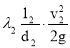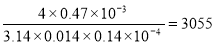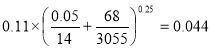Как решить задачу с баками с водой
Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Пусть за минуту в бак накачивается литров воды,
. Тогда за минуту выкачивается
л воды.
Составим таблицу по данным задачи:
| Производительность (л/мин) | Время (мин) | Объём работ (л) | |
|---|---|---|---|
| Накачивается | 117 | ||
| Выкачивается | 96 |
Так как на накачивание было затрачено на 5 мин. больше времени, составим уравнение:
,
Получаем квадратное уравнение:
,
имеющее корни: и
.
Отбрасывая отрицательный корень, находим, что за минуту в бак накачивается 9 л воды.
Источник
Как отмерить 4 литра воды с помощью двух вёдер по 5 и 3 литр? Задача для собеседования.
Эту задачу я узнал от одного коллеги, который пробовался на работу в Google. Он работал у нас Айтишником.
Однажды мы разговорились на тему собеседования, и наш диалог зашел про вопросы на тестировании для кандидатов.
Я считаю, что на собесе очень нервная остановка и на тестах кандидат не может себя проявить в полную меру.
На что мне мой коллега ответил, что это наоборот показывает стрессоустойчивость и способность сконцентрировать внимание на одной задачи, а если еще и оценить время, на которое он потратит на решение, то можно сделать много выводов.
Ну, не знаю он айтишник, может ему виднее.
Для примера он мне дал одну задачу, которую ему задавали при наборе в Google.
Эта задача начального уровня и кандидат на должность программиста должен с ней легко справляться за минуту.
После того, как он мне её показал, я тоже решил использовать у себя на собеседованиях, и оценивать за какое время её осилит мой будущий работник.
Задача очень легкая, и если он её не решает, дальше речи о трудоустройстве быть не может.
Условия задачи простые.
У вас есть два ведра по 5 и 3 литра, как с помощью этих этих емкостей можно отмерить ровно 4 литра воды? При этом количества воды и попыток не ограниченно.
Сейчас уже у моей команды есть много разных способов решения этой задачи, и они постоянно делятся ими со мной, вспоминая, как я их тестировал при приеме на работу.
Но больше всего их удивляло, что они шли на должность менеджеров по продажу, а их просили переливать воду. :))).
Используйте эту задачу при тестировании своих кандидатов, очень здорово помогает набирать правильных людей.
Ах, да, чуть не забыл сказать ответ на эту задачу.
Значит, что делаем, для того, чтобы у нас получилось 4 литра вода.
а) Наливаем в трехлитровое ведро до краев воды и переливаем в ведро 5 литров.
б) Далее еще раз набираем трехлитровое до края и дозаполняем два литра в пятилитровое до краев. Итого у нас в трехлитровом остается 1 литр воды.
в) Далее выливаем всю воду из пятилитрового ведра
г) Заливаем 1 литр из ведра в 3 литра в 5 литров, и теперь в 5 литровки у нас ровно 1 литр
д) Наливаем полное трехлитровое ведро и переливаем в 5-литровое.
Итого у на ровно 4 литра в 5- литровом ведре.
5 литровое ведро выливаем в трех литровое.
Итого остается 2 литра в пятилитровом.
Далее опустошаем трехлитровое и наливаем туда два литра из пятилитрового.
Наполняем до краев пятилитровое и переливаем недостающий литр в трехлитровое. Итого в пятилитровом ведре ровно 4 литра воды.
Источник
Примеры решенных задач по гидравлике — 3
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Для испытания на прочность резервуара с водой произведена опресовка под давлением p 1 . Через сутки давление, вследствие утечки из резервуара, понизилось до p 2 . Определить вел и чину утечки из резервуара, если модуль упругости воды Е = 2.03×10 9 Па. Резервуар имеет форму цилиндра диаметром d и высотой h .
Дано : p 1 =2.5 МПа ; p 2 =2 МПа ; d =1.5 м ; h =1.7 м.
Величину утечки определим из формулы коэффициента объёмного сжатия :
β w = 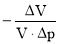
где V – первоначальный объём ; Δ V – изменение объёма при изменении давления на Δ p .
В данном случае величина утечки из резервуара равна величине изменения объёма, при изменении давления в резервуаре на Δ p . Тогда из (1) находим :
Здесь Δ p = p 2 — p 1 ; β w =1/ E ( где Е – модуль упругости воды) ; V = 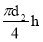
ΔV = 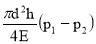
Вычисления по формуле (3) дают :
ΔV = 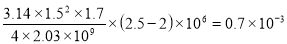
Цилиндрический сосуд диаметром D и высотой a , заполненный водой, опирается на плу н жер диаметром d . Определить показание манометра М и нагрузки на болтовые группы А и B , если масса верхней крышки сосуда m 1 , цилиндрической части сосуда m 2 и нижней крышки сосуда m 3 .
Дано : D =0.45 м ; a =0.65 м ; d =0.35 м ; m 1 =350 кг ; m 2 =200 кг ; m 3 =170 кг.
Найти : p м ; F A ; F B
Определим показание манометра :
p м = p 0 — p атм (1)
где p 0 – давление на свободной поверхности жидкости ; p атм – атмосферное давление ( p атм =10 5 Па) .
В данном случае p 0 равно давлению, производящим верхней крышкой сосуда :
p 0 = 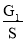
где G 1 – вес верхней крышки сосуда ; S – площадь свободной поверхности жидкости, ра в ный площади крышки диаметра D .
G 1 =m 1 g ; S=
С учётом выражений для G 1 и S формула (2) примет вид :
p 0 = 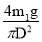
Подставляя (3) в (1), получим :
p м = 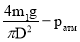
Вычисления по формуле (4) дают :
p м = 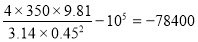
Т.е. манометр показывает вакуумметрическое давление p м =78.4 кПа.
Определим нагрузку на болтовые соединения группы А. Запишем ура внение равновесия для болтового соединения в проекции на вертикальную ось :
F A = P 0 — G 23 (5)
где P 0 – сила давления со стороны жидкости ; G 23 – вес цилиндрической и нижней частей сосуда .
P 0 = p 0 S ; G 23 =(m 2 +m 3 )g
Тогда выражение (5) примет вид :
F A = 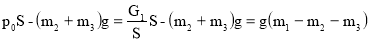
Вычисления по формуле (6) дают :
F A =9.81×(350-200-170)=-196.2 Н
Знак «минус» означает, что нагрузка F A направлена вниз.
Определим нагрузку на болтовые соединения группы B . Составляя уравнение равновесия болтовых соединений на вертикальную ось, получим :
где G 3 – вес ниж ней крышки сосуда ; N – сила давления жидкости на нижнюю крышку с о суда.
Силу давления на нижнюю крышку сосуда определим по формуле :
где S 1 = 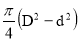
Подставляя (8) в (7) и, учитывая выражения для S 1 , p 0 и G 3 = m 3 g , получим :
F B = 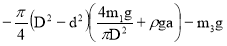
Вычисления по формуле (9) дают :
F B = 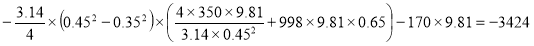
Знак «минус» означает, что нагрузка F B направлена вниз.
Ответ : p м =-7 8 . 4 кПа ; F A =-196.2 Н ; F B =-3424 Н.
Жидкость Ж подаётся в открытый верхний бак по вертикальной труде длиной l и диаме т ром d за счёт давления воздуха в нижнем замкнутом резервуаре.
Определить давление p воздуха, при котором расход будет равен Q . Принять следующие коэффициенты сопротивления : вентиля ξ в =8 ; входа в трубу ξ вх =0.5 ; выхода в бак ξ вых =1. эквивалентная шероховатость стенок трубы k э = 0.2 мм.
Дано : Ж – вода ; Q =10 л/с ; l =10 м ; d =80 мм.
Составим уравнение Бернулли для двух сечений 0-0 и 1-1 трубопровода :
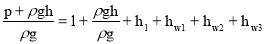
Отсюда находим давление воздуха p :
p= 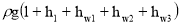
где p +ρ gh и ρ gh – давления в соответствующих сечениях ; p – давление воздуха ; ρ =998 кг/м 3 – пло т ность воды при t =20° C (табл. 1 [2]) ; h l – потери напора по длине трубопровода ; h w 1 , h w 2 , h w 3 – п о тери напора в местных сопротивлениях вентиля, вход в трубу , выход в бак.
Потери напора по длине трубопровода определим по формуле Вейсбаха-Дарси :
h l = 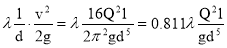
где λ – коэффициент гидравлического трения ; v – скорость жидкости в трубе ( v =4 Q /( π d 2 ) ; Q – расход ; l – длина трубопровода ; d – диаметр трубы.
Для нахождения коэффициента гидравлического трения λ, определим число Рейнольдса :
Re = 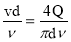
где ν=0.01 ×10 -4 м 2 /с – коэффициент кинематической вязкости воды при t =20° C ( по табл. 1 [2]) .
Вычисления по формуле (3) дают :
Re =
Для чисел Рейнольдса 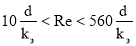
λ=
или с учётом формулы (3), получим :
λ =
Подставляя выражение для λ в формулу (2), получим :
h l = 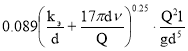
Потери напора в местных сопротивлениях находим по формулам :
h w 1 = 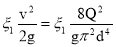
h w 2 = 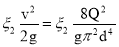
h w 3 = 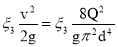
Подставляя (4), (5), (6) и (7) в формулу (1), получим :
p = 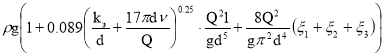
Вычисления по формуле (8) дают :
p =
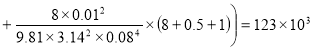
Ответ : p =123 кПа
Определить длину трубы l , при которой расход жидкости из бака будет в два раза меньше, чем через отверстие того же диаметра d . Напор над отверстием равен H . Коэффициент ги д равлического трения в трубе принять равным λ=0.025.
Дано : H =5 м ; d =50 мм ; Q 1 =0.5 Q 2 ; λ =0.025 .
Составим уравнение Бернулли для двух сечений трубы 0-0 и 1-1 :
H = 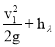
где v 1 – скорость в сечении 1-1 ; h λ – потери напора по длине тубы.
Потери напора определяются по формуле Вейсбаха-Дарси :
h λ = 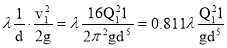
где λ – коэффициент гидравлического трения ; Q 1 расход в трубе.
Подставляя (2) в (1) и, учитывая что скорость v 1 связана с расходом Q 1 выражением :
v 1 = 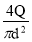
H =
Отсюда находим длину трубы :
l = 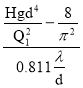
Расход через отверстие определяется выражением :
Q 2 = 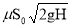
где μ =0.62 – коэффициент расхода ( рекомендации стр. 109 [1]) ; S 0 – площадь сечения о т верстия ( S 0 = π d 2 /4) ; H – напор, под которым происходит истечение (глубина погружения о т верстия под уровень жидкости в б а ке).
Учитывая, что по условию Q 1 = 0.5 Q 2 , то подставляя (4) в (3) и, учитывая выражение для S 0 , получим :
l = 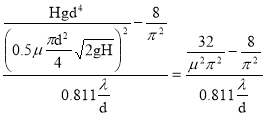
Вычисления по формуле (5) дают :
l= 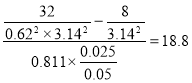
Центробежный насос с известной характеристикой откатывает воду из сборного колодца в бассейн с постоянным уровнем H по трубопроводам l 1 , d 1 и l 2 , d 2 . При работе насоса с пост о янным числом оборотов n =1450 мин -1 определить глубину h , на которой установится уровень воды в колодце, если приток в него Q . При расчётах принять коэффициенты гидравлического трения λ 1 =0.03 и λ 2 =0.035 и суммарные коэффициенты местных сопротивлений ζ 1 =6 и ζ 2 =10.
Дано : H =14 м ; l 1 =5 м ; d 1 =130 мм ; l 2 =11 м ; d 2 =80 мм ; Q =7 л / с.
Напор, развиваемый насосом, расходуется на подъём воды на геометрическую высоту H г = H + h и преодоление потерь напора во всасывающей и нагнетательной линиях :
H н = H г + h 1 +h 2 =H+h+h 1 +h 2
Отсюда глубина, на котором установится уровень воды в колодце :
h = H н — h 1 — h 2 (1)
где H н – напор, развиваемый насосом при заданном расходе Q ( определяется по граф и ку ; при Q =7 л / c , H =22 м) ; h 1 и h 2 – потери напора во всасывающей и нагнетательной линиях.
Потери напора состоят из потерь напора по длине и в местных сопротивлениях :
h 1 = h ℓ1 + h м1 ; h 2 = h ℓ2 + h м 2
Потери напора по длине определим по формуле Вейсбаха-Дарси :
h ℓ1 = 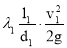
где λ – гидравлический коэффициент трения.
Скорость движения воды во всасывающей линии :
v 1 = 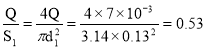
Скорость движения жидкости в нагнетающей линии :
v 2 = 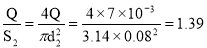
Потери напора по длине трубопровода для всасывающей линии :
h ℓ1 = 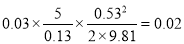
Потери напора по длине трубопровода для нагнетающей линии :
h ℓ2 = 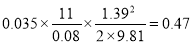
Потери в местных сопротивлениях по формуле Вейсбаха :
для всасывающей линии :
h м1 = 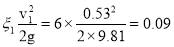
для нагнетающей линии :
h м2 = 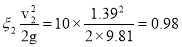
Общие потери во всасывающей линии :
h 1 =0.02+0.09=0.11 м.
Общие потери в нагнетающей линии :
h 2 =0 . 47+0.98=1 . 45 м.
Тогда, искомая глубина, на которой установится уровень воды в колодце :
h =22-0.11-1 . 45 = 20.44 м.
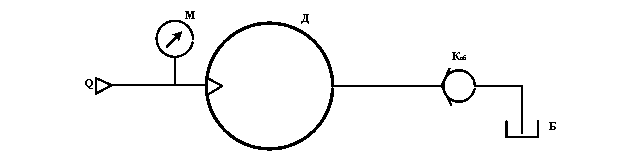
Вал гидродвигателя Д, рабочий объём которого V 0 , нагружен крутящим моментом М к . К двигателю подводится поток рабочей жидкости – масло Ж, температура которого 60°С, с расходом Q . КПД гидродвигателя : объёмный η 0 =0.96, гидромеханический η гм .
Определить частоту вращения вала гидродвигателя и показание манометра М, устано в ленного непосредственно перед двигателем, если потери давления в обратном клапане К об составляют Δ p кл =15 кПа. Длина линии равна l c , а диаметр d c . Эквивалентная шероховатость Δ э =0.05 мм.
Дано : Ж – индустриальное 20 ; Q =28 л / мин ; V 0 =40 см 3 ; M k =2 5 Н·м ; η гм =0.9 ; l c =2.8 м ; d c =14 мм.
Частоту вращения гидродвигателя определим по формуле :
n = 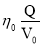
где η 0 – объёмный к.п.д. гидродвигателя ; Q – расход рабочей жидкость ; V 0 – рабочий объём гидродвигателя.
Вычисления по формуле (1) дают :
n = 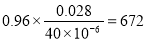
Определим показание манометра. Давление, создаваемое перед электродвигателем затр а чивается на потери давления в гидродвигателе Δ p , потери давления в обратном клапане Δp об , п о тери давления в сливной линии Δ p c :
p м =Δ p + Δp об +Δ p c (2)
Потери давления в гидродвигателе определим по формуле :
Δp = 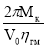
где М к – крутящий момент на валу двигателя ; η гм – к.п.д. гидродвигателя.
Вычисления по формуле (3) дают :
Δp = 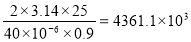
Потери давления в сливной линии определим по формуле :
где ρ – плотность рабочей жидкости ; h ℓ — потери напора в сливной линии.
Определим плотность рабочей жидк ости (масло индустриальное 20 ) при температуре t =60° по формуле :
ρ = 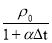
где ρ 0 =891 кг / м 3 (табл. 1 [2]) – плотность рабочей жидкости при t 0 =50° ; α =0.0007 1/° C (табл. 1 [2]) – температурный коэффициент расширения жидкости ; Δt = t — t 0 =60-50=10° — изм е нение температуры.
Тогда вычисления по формуле (5) дают :
ρ = 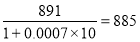
Потери напора в силовой линии по формуле Вейсбаха-Дарси :
h ℓ = 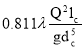
С учётом (6) формула (4) примет вид :
Δp = 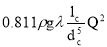
где λ – коэффициент гидравлического трения.
Коэффициент гидравлического трения λ определим по формуле Альтшуля :
λ = 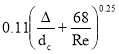
где Δ – эквивалентная шероховатость ; Re – число Рейнольдса.
Число Рейнольдса определим по формуле :
Re = 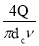
где ν=0 .14 ×10 -4 м 2 / с – кинематическая вязкость при t =60 ° (табл. 1 [2]) .
Вычисления по формуле (9) дают :
Re =
Тогда вычисления по формуле (8) дают :
λ =
Вычисления по формуле (7) дают :
Δp c = 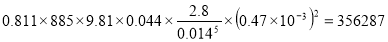
Окончательно, производя вычисления по формуле (2), найдём показания манометра :
p м =356+15+ 4361 = 4732 кПа
Ответ : n =672 об / мин ; p м =4732 к Па.
Имя файла: gidr4.doc
Размер файла: 1752.5 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
Источник