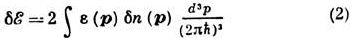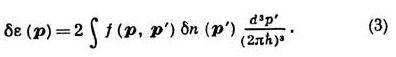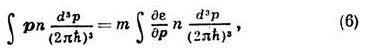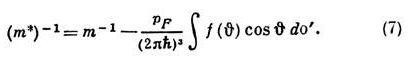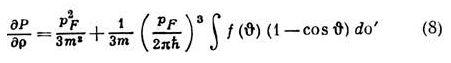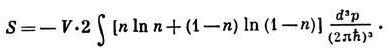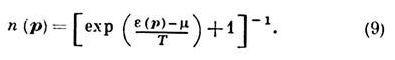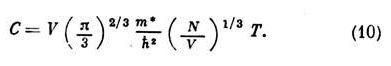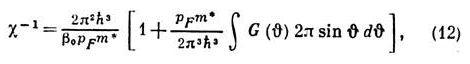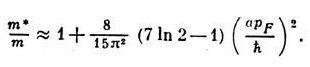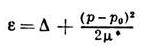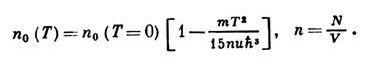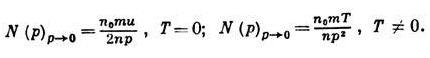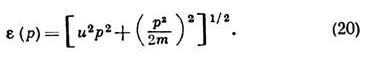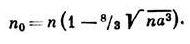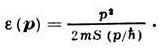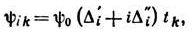Квантовая вода — с чем ее едят?

Мечта фермера – это поить простой водой птицу и животных и получать дополнительные надои и привесы, как от волшебных добавок. Мечта сегодня исполняется: разработан аппарат «Умелец-нано», который производит квантование и нано-дисперсию воды воздухом. Что это дает живому организму? Организм начинает «дышать всем телом», воздух попадает в кровь не только из легких, но и из воды и обеспечивает полноценное дыхание всех клеток. Вода отдает энергию митохондриям, энергия клетки повышается. Для животных – это повышение надоев и привесов, для спортсменов – это допинг.
Как вода становится квантовой?
Вода всегда была веществом квантовым. Ее состояние изменяется с изменением орбит электрона в водороде. Водород – единственный элемент в системе вещества вселенной, где электрон может переходить с орбиты на орбиту до 7раз. Вот оттуда и число 7 стало волшебным, потому что все изменения в организме — это прежде всего изменение состояния воды, которой в организме до 75%.
В молекулярном деструкторе вода получает дополнительную энергию, а куда она ее денет, как она ее запрячет? Она может принять квант энергии, а для этого изменит орбиту электрона. Угол между атомами водорода в воде изменится, изменится кластерное состояние воды. Вода стала квантовой, присоединила энергию, изменила энергетическое состояние. Когда она отдаст эти кванты в организме, энергия перейдет в энергию клетки, без каких-либо химический или физических преобразований, на которое будет затрачена энергия. А уже позднее, мы получим привесы и надои от применения квантовой воды. Повышение энергии организма повышает и иммунный статус, животное становится более энергичным, энергии то хватает.
Как проверить изменение в воде?
Сегодня есть приборы, которыми можно измерить ОВП, РН, состояние солей в воде. Технология нано-дисперсии позволяет эти параметры менять. Какие показатели будут, не пишу, потому, так как вода у все разная, состояние солей разное и показатели будут разные. Приборы недорогие, можно купить и фиксировать, при каких показателях у вас будут получатся лучшие привесы и надои, именно на вашей воде. А они будут, потому что насыщение воздухом крови у спортсменов запретили, это допинг, мышцы работают более эффективно. У животных строение мышц не отличается от человеческих.
Что дает квантовая вода с эффектом нано-дисперсии воздухом животному или птице и насколько возможен подъем в весе или надоях?
Эффективность применения энергии воды в кормлении животных и птицы дает возможность получать дополнительные привесы или надои до 30%, просто на воде. Но у всех будет эффект разный, это зависит от того, насколько интенсивно Вы уже эксплуатируете животное.
Но эффект на уровне 10-15% будет у всех. Вспомните спортсменов с их переливанием крови перед соревнованиями: допинг кислородом дает возможность прыгнуть выше, пробежать быстрее, но конечно не в два–три раза. При этом эксплуатация организма у спортсмена уже очень высокая.
Вывод. Нужно применять квантовую воду и ЗЦМ-нано уже сегодня и получать дополнительную прибыль.
Источник
Квантовая жидкость
КВАНТОВАЯ ЖИДКОСТЬ — жидкость, на свойства к-рой существ. влияние оказывают квантовые эффекты в поведении составляющих её частиц. Квантовые эффекты становятся существенными при очень низких темп-pax, когда волна де Бройля частиц, отвечающая их тепловому движению, становится сравнимой с расстоянием между ними и происходит квантовое вырождение жидкости. С понижением темп-ры роль квантовых эффектов увеличивается, и при достаточно низкой темп-ре любая жидкость должна была бы стать квантовой. Однако подавляющее большинство обычных жидкостей затвердевает раньше, чем квантовые эффекты начинают проявляться сколько-нибудь заметно. Поэтому фактически в прямом лаб. эксперименте приходится иметь дело с двумя К. ж.изотопами гелия: жидким 4 Не и жидким 3 Не (а также с их смесями) при темп-pax
1-2 К. К. ж., по-видимому, образуют нейтроны в нейтронных звёздах. В определ. смысле К. ж. составляют электроны в металлах и полупроводниках и экситоны в экситонных каплях в диэлектриках, а также протоны и нейтроны в атомных ядрах. К. ж. классифицируют по статистике составляющих их частиц. Жидкость, состоящая из частиц с целым спином, бозонов (жидкий 4 Не), наз. бозе-жидкостью, а из частиц с полуцелым спином, фермионов (жидкий 3 Не),ферми-жидкостью.
Элементарные возбуждения. Квантовые эффекты особенно ярко проявляются при низких темп-pax, когда жидкость находится в слабовозбуждённых состояниях, близких к основному квантовому состоянию. Выявление свойств таких состояний — осн. задача теории К. ж. Важнейшее положение этой теории состоит в том, что переход пространственно-однородной К. ж. из осн. состояния в слабовозбуждённое можно описать как появление в ней газа квазичастиц, или элементарных возбуждений, каждое из к-рых обладает определёнными импульсом и энергией. Энергия квазичастицы e определяется её импульсом р. Зависимость e(р)закон дисперсии квазичастиц — является важнейшей характеристикой К. ж. Всякое слабовозбуждённое состояние жидкости характеризуется распределением квазичастиц по импульсам. Кроме импульса состояние квазичастицы в изотропной К. ж. характеризуется спиральностью — проекцией угл. момента на направление импульса. Квазичастицы, отличающиеся знаком спиральности, в жидкости, инвариантной относительно пространственной инверсии, имеют одну и ту же энергию, т. е. состояния квазичастиц с отличной от нуля спиральностью двукратно вырождены. Как и обычные частицы, квазичастицы подчиняются определ. статистикеБозе — Эйнштейна статистике или Ферми — Дирака статистике. Квазичастицы с целой (включая нуль) спиральностью являются бозонами, с полуцелой — фермионами. При этом поскольку проекция угл. момента жидкости может меняться лишь на целое число (в единицах h), фермиевские квазичастицы могут появляться и исчезать лишь парами квазичастица-дырка (аналогичными в известном смысле электрон-позитронным парам), а бозевские — поодиночке. В бозе-жидкости все квазичастицы являются бозонами, тогда как среди частиц ферми-жидкости могут быть как фермиевские, так и бозевские ветви. В состоянии термодинамич. равновесия квазичастицы фермиевского и бозевского типов распределены по импульсам согласно ф-циям распределения идеальных (соответственно) фермии бозе-газов. Описание возбуждённых состояний жидкости на языке квазичастиц является приближённым. Это проявляется в конечности времени жизни квазичастиц, обусловленной их взаимодействием. При отличных от абс. нуля темп-pax затухание квазичастиц связано с процессами их взаимного рассеяния и распада. При темп-ре абс. нуля рассеяние отсутствует и затухание квазичастицы связано только с процессами распада; если в том или ином интервале импульсов они запрещены законами сохранения, квазичастица является строго незатухающей.
Ферми-жидкость. Нормальная (несверхтекучая) фермиевская жидкость имеет спектр квазичастиц, аналогичный спектру идеального ферми-газа. Его естественно описывать, считая, что при темп-ре абс. нуля квазичастицы заполняют в импульсном пространстве все квантовые состояния вплоть до нек-рого фермиевского импульса pF. Рождение пары квазичастица (с импульсом р) — дырка (с импульсом р‘) описывается в этой картине как переход квазичастицы с импульсом -р‘, первоначально находившейся внутри фермиевской сферы, в состояние с импульсом р вне этой сферы. Т. о., квазичастицы могут иметь импульсы p>pF, a дырки pF. Важнейшее положение теории ферми-жидкости, созданной Л. Д. Ландау в 1956, состоит в том, что определяющий распределение квазичастиц фермиевский импульс рF связан с плотностью числа реальных частиц (атомов жидкости) N/V тем же соотношением, что и в идеальном ферми-газе:
pF = h(3p 2 ) 1/3 (N/V) 1/3 (1)
(N — число частиц, V — объём системы). В этом смысле число квазичастиц в ферми-жидкости равно числу реальных частиц жидкости. Энергия E ферми-жидкости является функционалом от функции распределения квазичастиц п(р); её изменение при изменении п(р)определяет энергию квазичастицы e(р):
(здесь и далее предполагается, что распределение квазичастиц не зависит от их спиновых состояний, и опускаются спиновые индексы у всех величин). Важное отличие ферми-жидкости от идеального ферми-газа состоит в том, что энергия квазичастицы e(p) зависит от распределения всех остальных квазичастиц. Изменение e(р) при малом изменении п(р)имеет вид
Ф-ция f(p, р‘)описывает взаимодействие между квазичастицами. Фермиевский импульс рF связан с химическим потенциалом m жидкости равенством:
(eF — ферми-энергия). В окрестности фермиевского импульса
e(р)
где vF — скорость квазичастиц на фермиевской сфере. Отношение m*=pF/vF наз. эффективной массой квазичастицы. Ввиду равенства числа частиц числу квазичастиц плотность импульса последних, делённая на массу частицы т, должна быть равна потоку их числа, что приводит к соотношению
варьирование к-рого по п даёт связь эфф. массы с ф-цией взаимодействия f:
Здесь ф-ция f(p, р’)берётся при |p|=|p’|=pF, и поэтому она зависит лишь от угла q между р и р‘, do’=2p sin qdq — элемент телесного угла в направлении р‘. Аналогично можно получить связь ф-ции f с сжимаемостью жидкости:
(r=mN/V — плотность жидкости, Р — давление). Энтропия жидкости выражается через ф-цию распределения квазичастиц той же ф-лой, что и для идеального ферми-газа:
Распределение же квазичастиц по импульсам в состоянии термодинамич. равновесия даётся обычной ф-лой распределения Ферми — Дирака (используется система единиц, в к-рой темп-pa Т выражается в энергетич. единицах, т. е. в к-рой k=1):
Это приводит к линейному по темп-ре закону теплоёмкости ферми-жидкосги:
Время жизни квазичастиц в ферми-жидкости определяется процессами их рассеяния. При абс. нуле темп-р они сводятся к рождению пар частица-дырка, причём вероятность такого рассеяния (с учётом принципа Паули) для квазичастицы с импульсом р пропорц. (р-рF) 2 . Поэтому реальный физ. смысл имеют лишь квазичастицы вблизи поверхности Ферми, где эта вероятность мала. Аналогично ср. длина пробега квазичастиц при конечных темп-pax l
Т -2 , так что фермиевская жидкость при низких темп-pax в кинетич. отношении ведёт себя как разреж. газ и должна описываться кинетическим уравнением. Теплопроводность ( и вязкость h ферми-жидкости с понижением темп-ры изменяются след. образом:
Соответственно с понижением темп-ры возрастает затухание звука, так что при Т=0 распространение обычного звука невозможно. Возможно, однако, распространение колебаний особого рода — нулевого звука, в к-ром происходит сложная деформация ф-ции распределения квазичастиц. Закон дисперсии этих колебаний, как и у обычного звука, линейный: w=u0k (где w — частота колебаний, k — волновое число), но скорость их распространения и0 не выражается непосредственно через сжимаемость (8), а требует для своего определения решения кинетич. ур-ния. Затухание нулевого звука пропорц. большей из величин (hw) 2 и Т 2 и при низких темп-pax мало. Нулевой звук представляет собой бозевскую ветвь спектра возбуждений ферми-жидкости. От распределения по импульсам квазичастиц, даваемого ф-лой (9), следует отличать распределение по импульсам реальных частиц. Последнее размыто даже при Т=0, однако, как и распределение квазичастиц, имеет резкий скачок при p=pF Для описания магн. свойств ферми-жидкости необходимо рассматривать ф-ции распределения частиц, зависящие от проекции их спинов на направление магн. поля. При этом ф-ция взаимодействия f является матрицей по спиновым индексам взаимодействующих частиц, к-рую в пренебрежении слабыми релятивистскими (спин-орбитальным и спин-спиновым) взаимодействиями можно записать в виде
f = Ij(р, p’) + ss’G(p, р‘), (11)
где I — единичная матрица, s и s’ — Паули матрицы ,действующие на спиновые индексы частиц с импульсами р и р’, j и G — скалярные ф-ции. Магн. восприимчивость c ферми-жидкости при низких темп-pax стремится к пост. пределу:
где b0 — магн. момент изолированной частицы. С микроскопич. точки зрения ф-ция взаимодействия f представляет собой амплитуду рассеяния квазичастиц «вперёд», когда передача энергии hw и передача импульса hk стремятся к нулю. Предельное значение амплитуды зависит от порядка перехода к указанному пределу, и ф-ция f выражается через амплитуду, когда w, k и k/w стремятся к нулю. Последоват. микроскопич. вычисление параметров ферми-жидкости возможно лишь в случае разреж. системы, т. е. ферми-газа ,когда ср. расстояние между частицами велико по сравнению с длиной рассеяния а частиц друг на друге:
В этом случае все характеристики системы можно определить, используя теорию возмущений. В частности, для эфф. массы имеем:
Бозе-жидкость. В области самых малых импульсов квазичастицы в бозе-жидкости являются фононами — квантами звука с законом дисперсии
где и — скорость звука, связанная со сжимаемостью жидкости при Т=0 обычной ф-лой:
Соответственно теплоёмкость жидкости при самых низких темп-pax имеет вид
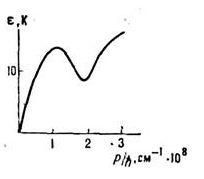
Ход кривой спектра e(р) при не малых значениях импульса определяется конкретными свойствами взаимодействия атомов. В реальном 4 Не эта кривая, измеренная экспериментально с помощью неупругого рассеяния медленных нейтронов, имеет форму, показанную на рисунке. Фактически вклад в термодинамич. ф-ции жидкости, кроме начальной — фононной — части, вносят квазичастицы вблизи минимума кривой — ротоны, где кривая может быть представлена в виде
с эксперим. значениями параметров: D=8,7 К, р0/h=1,9.10 8 см -1 , m* = 1,1.10 -24 г. При нормальном давлении д 2 e/др 2 |р»0>0. Это приводит к тому, что фононы нач. части кривой могут распадаться на фононы с меньшими импульсами, что даёт при малых р затухание
р 5 . Большая же часть кривой при T=0 является незатухающей. При р
1,5р0 кривая e(р) достигает значения 2D. В этой точке появляется возможность распада квазичастицы на два ротона с энергиями D каждый. При этом значении импульса кривая e(р) обрывается. Важнейшим свойством бозевской жидкости при низких темп-pax является её сверхтекучесть — способность двигаться относительно сосуда без диссипации энергии. Как показал Л. Д. Ландау (1941), это свойство тесно связано с видом спектра квазичастиц. Диссипация энергии при абс. нуле темп-ры означает рождение квазичастиц при движении. Однако для спектра, показанного на рис., такой процесс невозможен при достаточно малой скорости движения в силу законов сохранения энергии и импульса. Действительно, пусть жидкость движется относительно сосуда со скоростью V. Тогда если энергия квазичастицы в неподвижной жидкости есть e(р), то в системе координат, связанной с сосудом, её энергия равна e(p)+pV, согласно закону преобразования энергии в нерелятивистской механике. Рождение квазичастиц, связанное с диссипацией энергии, возможно, если последнее выражение отрицательно при каких-то значениях р, т. е. если скорость движения больше критич. скорости Vc (критерий Ландау):
Если правая часть выражения (17) отлична от нуля, как это имеет место для реального спектра гелия, показанного на рис., диссипация отсутствует при всех скоростях, меньших Vc. При Т=0 вся жидкость движется как сверхтекучая. При конечных темп-pax совокупность квазичастиц движется как обычная жидкость — это «нормальная часть», с к-рой связана нек-рая плотность нормальной части жидкости rn. Остальная часть плотности rs=r-rn движется как сверхтекучая жидкость. По мере увеличения темп-ры р„ увеличивается, и при нек-рой темп-ре T=Tl(Р), зависящей от давления, rs обращается в нуль и жидкость теряет свойство сверхтекучести. Линия T=Tl(Р) является линией фазовых переходов второго рода. Для 4 Не при давлении насыщенных паров Tl=2,18 К. Вблизи темп-ры перехода rs обращается в нуль по закону: rs
— 0,01 — критич. показатель теплоёмкости.
Своеобразными особенностями обладает распределение по импульсам истинных частиц — атомов жидкости. При Т
где n0 — плотность числа частиц в конденсате, j — фаза. y можно рассматривать как комплексный параметр порядка, наличие к-рого отличает сверхтекучую фазу от нормальной. Плотность числа частиц п0 не связана непосредственно с rs, однако она обращается в нуль одновременно с rs в точке перехода, хотя и по несколько иному закону: n0
(Tl — T) 2b , где b — критич. показатель параметра порядка. Фаза же волновой ф-ции конденсата определяет скорость сверхтекучей части бозе-жидкости (сверхтекучую скорость):
(m — масса атома). При низких темп-pax п0 уменьшается с повышением темп-ры по закону:
Распределение по импульсам частиц, не находящихся в конденсате, имеет особенность в области малых импульсов:
Особый характер имеет вращение сверхтекучей части бозе-жидкости. Оно происходит вокруг отд. вихревых нитей, циркуляция скорости вокруг к-рых, в силу (19), квантована и равна целому кратному от 2ph/m. Микроскопич. вычисление параметров бозе-жидкости возможно также лишь в пределе разреж. системы, удовлетворяющей условию (13), т. е. бозе-газа. Для такого газа спектр квазичастиц для любых значений р определяется ф-лой Боголюбова (Н. Н. Боголюбов, 1947):
При малых р спектр (20) имеет вид (14), причём скорость звука и равна и=(4ph 2 па/m 2 ) 1/2 . При р » : (20) переходит в спектр свободных атомов р 2 /2m. Плотность числа атомов в конденсате при Т=0 в этой модели равна
Для реальной жидкости можно получить приближённую интерполяц. ф-лу Фейнмана, связывающую спектр возбуждений со статпч. формфактором жидкости S(k), к-рый можно определить по рассеянию рентгеновских лучей жидкостью:
Согласно этой ф-ле, ротонному минимуму соответствует максимум S (k), связанный с ближним порядком в расположении атомов жидкости.
Сверхтекучая ферми-жидкость. При достаточно низких темп-pax состояние нормальной ферми-жидкости оказывается неустойчивым, если взаимодействие между квазичастицами имеет характер притяжения. Более точно, неустойчивость возникает, если амплитуда рассеяния квазичастиц с противоположными импульсами имеет соответствующий притяжению отрицат. знак хотя бы при одном значении относит. угл. момента I квазичастиц. Тогда с понижением темп-ры при нек-рой критич. темп-ре Тс происходит «спаривание» — образование молекулоподобных куперовских пар квазичастиц с противоположными импульсами. Эти пары являются бозонами и в нек-рых отношениях ведут себя как бозевский конденсат. Темп-pa перехода Тс экспоненциально зависит от амплитуды для соответствующего l. Ниже Тс ферми-жидкость становится сверхтекучей. Конкретные свойства сверхтекучей фазы зависят от значения момента, при к-ром происходит спаривание. Если спаривание происходит в состоянии с l=0, то жидкость остаётся изотропной. Волновая ф-ция электронных пар является в этом случае скаляром вида (18). Спектр квазичастиц ниже точки перехода меняется и приобретает вид
Из (21) видно, что в спектре имеется «щель»: мин. энергия, необходимая для рождения квазичастицы, равна D (а пары частица-дырка 2D). Щель D зависит от темп-ры и обращается в нуль при Т=Тc. При Т=0 D=1,75Tc Благодаря наличию щели в спектре теплоёмкость, соответствующая фермиевской ветви возбуждений (21), при низких темп-pax экспоненциально мала. Система, однако, имеет и бозевскую ветвь возбуждений — обычный звук с законом дисперсии (14) — (15), так что теплоёмкость при низких темп-pax определяется законом (16). Спектр (21) удовлетворяет условию сверхтекучести с конечным значением Vс. Само это условие не является необходимым для сверхтекучести ферми-жидкости, поскольку неогранич. рождение фермиевских квазичастиц запрещено принципом Паули. Однако его выполнение обеспечивает равенство rn=0 при T = 0. Аналогичными свойствами, осложнёнными наличием электрич. заряда и анизотропией, обладают электроны в сверхпроводящей фазе металлов (см. Сверхпроводимость). Реальный 3 Не переходит в сверхтекучее состояние с темп-рой перехода при нулевом давлении Tc
10 -4 К. Спаривание происходит в состояние с l=1 и спином 1. Параметр порядка — волновая ф-ция пар — может быть в этом случае представлен в виде тензора второго ранга yik, первый индекс к-рого относится к орбитальным, а второй — к спиновым переменным. Сверхтекучий 3 Не является, т. о., жидким кристаллом. Существуют две фазы сверхтекучего 3 Не — Аи B-фазы, отличающиеся видом тензора yik. Низкотемпературная B-фаза более изотропна, её анизотропия связана лишь с относительно слабым взаимодействием спинов ядер атомов 3 Не с их орбитальным движением. В пренебрежении этим взаимодействием тензор yik можно привести к виду yik= y0dik где y0 — нек-рый скалар (dik — символ Кронекера). Спектр квазичастиц имеет вид (21) с не зависящей от углов щелью D. A-фаза существенно анизотропна. Тензор yik для неё можно привести к виду
где Di‘, Di», tk — компоненты единичных вещественных векторов D’, D», t. Векторы D’ и D» ортогональны и их векторное произведение l определяет направление орбитальных моментов всех куперовских пар. Вектор t определяет направление, на к-рое проекция спинов пар равна нулю. Спектр возбуждений А-фазы имеет вид (21), однако щель зависит от угла q между направлением импульса р и вектором l:D 2
sin 2 q. Лит.: Абрикосов А. А., Горьков Л. П., Дзялошинский И. Е., Методы квантовой теории поля в статистической физике, М., 1962; Пайнс Д., Нозьер Ф., Теория квантовых жидкостей, пер. с англ., М., 1967; Сверхтекучесть гелия-3. Сб. ст., пер. с англ., М., 1977; Л и ф ш и ц Е. М., Питаевский Л. П., Статистическая физика, ч. 2 — Теория конденсированного состояния, М., 1978; Квантовые жидкости и кристаллы, Сб. ст., пер. с англ., М., 1979. Л. П. Питаевский.
Источник