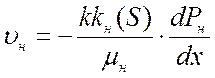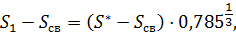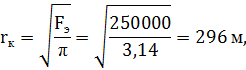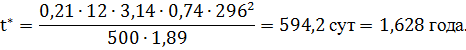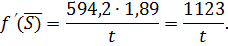3.2. Модели вытеснения нефти
Рассмотрим модели процесса вытеснения нефти водой (газом).
3.2.1. Модель поршневого вытеснения.
Предполагается движущийся в пласте вертикальный фронт (границы), впереди которого нефтенасыщенность равна начальной (
), а позади остается промытая зона с остаточной нефтенасыщенностью
. На рис. 25 схематически показан профиль насыщенности при
фиксированном положении фронта 
. Перед фронтом фильтруется только нефть, а позади— только вода.
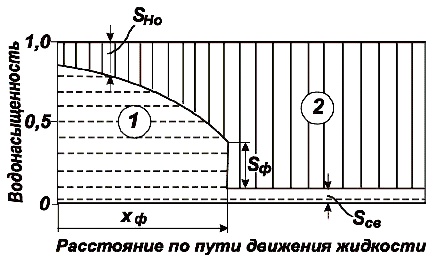
Рис. 25. Модель поршневого вытеснения нефти водой. Насыщенность: 1- водой; 2 – нефтью
В соответствии с этой моделью полное обводнение продукции скважин должно произойти мгновенно в момент подхода фронта вытеснения к скважинам.
3.2.2. Модель непоршневого вытеснения
По схеме Бакли — Леверетта предполагается в пласте движущийся фронт вытеснения. Скачок нефтенасыщенности на нем значительно меньше, чем при поршневом вытеснении.
Рис. 26. Модель непоршневого вытеснения нефти водой. Насыщенность: 1- водой; 2 – нефтью
Перед фронтом вытеснения движется только нефть, позади него — одновременно нефть и вода со скоростями, пропорцио-нальными соответствующим фазовым проницаемостям. Причем по мере продвижения фронта вытеснения скорости изменяются не только в зависимости от насыщенности в пласте, но и во времени. В момент подхода фронта к скважине происходит мгновенное обводнение до некоторого значения, соответствующего скачку нефтенасыщенности на фронте Sф, а затем обводненность медленно нарастает.
3.3. Уравнение неразрывности
Выведем вначале уравнение неразрывности массы вещества при его одномерном прямолинейном движении в пласте. Масса 
вещества плотностью
в элементе пласта (рис. 27) длиной
, толщиной
и шириной
, измеряемой в направлении, перпендикулярном к плоскости при пористости пласта
, составит
(3.11)
Рис. 27. (С лева)Схема элементарного объема прямолинейного пласта
Рис. 28. (С права) Схема элементарного пласта в трехмерном случае
Если считать, что в элемент пласта через его левую грань поступает вещество с массовой скоростью 
, вытесняется из элемента с массовой скоростью и
, а накопленный объем его
за время
, получим с учетом того, что в элемент вошло больше вещества, чем из него вышло:
. (3.12)
(3.13)
при 
(3.14)
Уравнение (3.14) и есть уравнение неразрывности массы вещества в пласте при одномерном прямолинейном движении насыщающего его вещества. Чтобы получить такое уравнение для трехмерного случая, необходимо рассмотреть баланс массы в объемном элементе пласта 
(рис. 28). Рассматривая массовые скорости поступления вещества в куб и вытеснения из него, а также накопленный объем его в кубе, получим
. (3.15)
Уравнение (3.15) можно записать также в следующем общем виде:
. (3.16)
Уравнения (3.15), (3.16) — уравнения неразрывности массы вещества во время его движения при трехмерном измерении. Если в пласте одновременно движутся несколько веществ, находящихся как в газовой, так и в жидкой фазе, составляют уравнения неразрывности массы каждого вещества (компонента) в соответствующих фазах.
Источник
Модель непоршневого вытеснения
По схеме Бакли — Леверетта предполагается в пласте движущийся фронт вытеснения.
Рис. 26. Модель непоршневого вытеснения нефти водой. Насыщенность: 1- водой; 2 – нефтью
Перед фронтом вытеснения движется только нефть, позади него — одновременно нефть и вода со скоростями, пропорциональными соответствующим фазовым проницаемостям. Причем по мере продвижения фронта вытеснения скорости изменяются не только в зависимости от насыщенности в пласте, но и во времени. В момент подхода фронта к скважине происходит мгновенное обводнение до некоторого значения, соответствующего нефтенасыщенности на фронте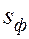 
, а затем обводненность медленно нарастает.
Распределение водонасыщенности в пласте изменяется по мере продвижения в глубь пласта фронта вытеснения таким образом, что значения водонасыщенности на фронте вытеснения Sф и на входе в пласт остаются неизменными. Таким образом, кривая распределения водонасыщенности как бы «растягивается» оставаясь подобной себе. Такое распределение водонасыщенности называется автомодельным.
При непоршневом вытеснении добыча нефти из пласта продолжается и после прорыва фронта вытеснения к концу пласта.
На практике при разработке нефтяных месторождений из добывающих скважин сначала получают практически чистую нефть, т.е. безводную продукцию, а затем, по мере роста закачиваемой в пласт воды начинают вместе с нефтью добывать воду.
МЕТОДИКИ РАСЧЕТОВ ФИЛЬТРАЦИИ ФЛЮИДОВ В НЕОДНОРОДНЫХ ПЛАСТАХ
Внедрение новых технологий разработки в нефтяную промышленность проводят после того, как оно прошло изучение в лабораторных условиях. В свое время прошло эту стадию и такое широко развитое на практике воздействие на нефтяные пласты, как заводнение. За стадией лабораторного исследования следуют первые промышленные испытания процессов.
В этот период нужно количественное представление о технологии, т.е. создание моделей.
Весь процесс разработки нефтяных месторождений описывается системами дифференциальных уравнений с начальными и граничными условиями. Расчеты, проводимые на основе моделей, называют методиками расчета.
Дифференциальные уравнения, описывающие процессы разработки основаны на использовании двух законов природы: закона сохранения вещества и закона сохранения энергии, а также на специальных законах фильтрации.
Закон сохранения вещества в моделях разработки записывается в виде дифференциального уравнения неразрывности массы вещества, либо в виде формул, выражающих материальный баланс веществ в целом в пласте. В последнем случае метод расчета получил название метода материального баланса.
Закон сохранения энергии используют в моделях разработки в виде дифференциального уравнения сохранения энергии движущихся в пластах веществ.
Основным законом фильтрации однородной жидкости или газа является закон Дарси, т.е. скорость фильтрации линейно и прямо пропорционально зависит от градиента давления.
, где
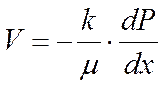
V – скорость фильтрации жидкости, м/сек;
k — коэффициент проницаемости, м 2 ;
µ — вязкость жидкости в пластовых условиях, мПа·с;
— градиент давления в рассматриваемой точке х.
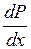
В случае фильтрации неоднородной жидкости, например, нефть и вода справедлив закон 2х фазной фильтрации. Тогда формула записывается в следующем виде:
,
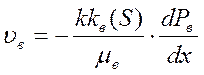
где υн, υв – вектор скорости фильтрации соответственно нефти и воды;
kн (S), kв (S) – относительные проницаемости для нефти и воды, зависящие от водонасыщенности S;
Рн, Рв – давление для нефти и воды.
Вспомним, что относительная проницаемость пористой среды это отношение фазовой проницаемости для данной фазы к абсолютной.
Фазовая это проницаемость пород для данной жидкости при наличии или движении в порах многофазных систем.
Абсолютная проницаемость это проницаемость пористой среды, которая определена при наличии в ней лишь одной фазы.
Исследования показывают, что фазовая и относительная проницаемость для различных фаз зависит от нефте-газонасыщенности породы
Если часть пор занята какой либо фазой, то ясно, что проницаемость породы для другой фазы становится меньше.
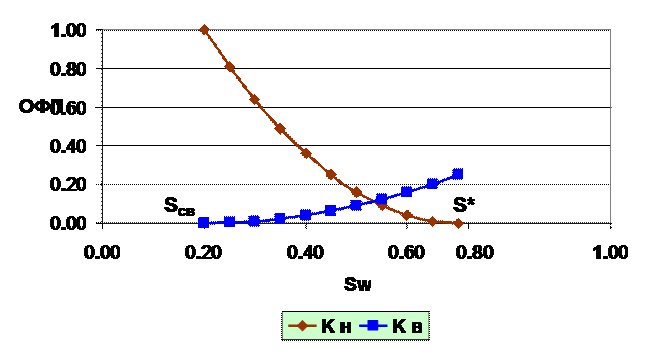
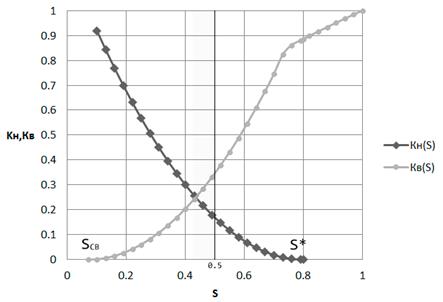
График относительных фазовых проницаемостей для нефти и воды имеет вид, представленный на рисунке. На оси абсцисс отмечены 2 характерные точки Sсв. и S*
Sсв.- это связанная вода, которой содержится в породе около 20%. Относительная проницаемость для нее в данной точке будет равняться 0, несмотря на то, что она в пласте присутствует, но добыть ее мы не можем, так как она раздроблена, находится в тупиковых зонах.
Если в породах содержится 30% связанной воды, то относительная проницаемость для нефти уменьшается в 2 раза. Поэтому 
необходимо применять меры для предохранения нефтяных пластов и забоев скважин от преждевременного обводнения.
Из рисунка видно, что в точка S* при водонасыщенности 80%, относительная проницаемость для нефти равна 0, хотя нефть в пласте имеется. При вытеснении нефти водой остаточная нефтенасыщенность составляет не менее 20%, так как нефть прочно удерживается в породе капиллярными силами, диспергирована и также находится в тупиковых зонах.
Аналогичные зависимости имеются и для трехфазной фильтрации жидкости и газа, когда в пласте происходит одновременная фильтрация нефти, воды и газа.
Методики расчетов в зависимости от количества фильтрующихся фаз подразделяются на: а) однофазные; б) двухфазные; в) трехфазные.
В зависимости от формы выделенного расчетного элемента методики гидродинамических расчетов делятся на:
Современные методики расчетов применяют двумерные трехфазные или трехмерные трехфазные.
Источник
Модель непоршневого вытеснения нефти
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Модель непоршневого вытеснения нефти
Модель непоршневого вытеснения нефти водой – это гидродинамическая
модель процесса заводнения, основанная на теории совместной фильтрации не-
однородных несмешивающихся жидкостей.
Первое решение задачи двухфазной фильтрации было получено амери-
канскими исследователями Бакли и Левереттом для двух несмешивающихся
несжимаемых жидкостей при пренебрежении гравитационными и капиллярны-
Для большинства пластов при вытеснении из них нефти водой характерно
возникновение в порах раздробленных (диспергированных) глобул нефти. Если
в единице объема пористой среды содержится сравнительно небольшое число
тупиковых зон, то нефть будет продолжать двигаться позади фронта вытесне-
ния вместе с водой и извлекаться из пласта по мере его заводнения. Таким об-
разом, вода не заполняет полностью область, первоначально занятую нефтью. В
этой области происходит совместное движение двух жидкостей – вторгшейся
воды и оставшейся, постепенно вымываемой нефти.
В отличие от модели поршневого вытеснения, согласно которой из об-
воднившихся пропластков нефть не извлекается, модель непоршневого вытес-
нения учитывает совместную (двухфазную) фильтрацию нефти и воды в порис-
той среде. При этом водонасыщенность в каждом сечении заводненной области
непрерывно увеличивается, достигая предельного значения S*.
Модель процесса непоршневого вытеснения нефти водой позволяет дос-
таточно точно рассчитывать показатели разработки пласта в период добычи об-
водненной продукции даже в сочетании с моделью однородного пласта. В ее
основе лежат зависимости относительных фазовых проницаемостей для нефти
и воды от водонасыщенности S.
Типы моделей пластов
Модели пластов условно подразделяют на детерминированные и вероятностно-статистические.
Детерминированные модели – это такие модели, в которых стремятся воспроизвести как можно точнее фактическое строение и свойства пластов, как бы создавая «фотографию» пласта. При расчете процессов разработки месторождения с использованием детерминированной модели всю площадь пласта или его объем разбивают на определенное число ячеек и каждой ячейке придают те свойства, которые присущи пласту в области ее расположения. Дифференциальные уравнения разработки месторождения заменяют конечно-разностными соотношениями, а затем производят расчет с помощью вычисли-
Вероятностно-статистические модели не отражают детальные особенно-
сти строения и свойства пластов, но количественно характеризуют их главные
особенности. К числу наиболее известных вероятностно-статистических моде-
лей пластов относятся модели однородного, слоистого, трещиноватого и тре-
В модели однородного пласта основные параметры реального пласта
(пористость, проницаемость), изменяющиеся от точки к точке, осредняют. Час-
то, используя модель такого пласта, принимают гипотезу и о его изотропности,
т.е. о равенстве проницаемостей в любом направлении, исходящем из рассмат-
риваемой точки пласта. Однако иногда пласт считают анизотропным. При этом
принимают, что проницаемость пласта по вертикали (главным образом, вслед-
ствие напластования) отличается от его проницаемости по горизонтали.
Модель слоистого пласта представляет собой структуру (пласт), состоящую из набора слоев с пористостью и проницаемостью. При всем этом считают, что из всей толщины пласта слои с пористостью и проницаемостью составляют часть и т.д.
Модель трещиноватого пласта. Если нефть в пласте залегает в трещинах, разделяющих непористые и непроницаемые блоки породы, то модель такого пласта может быть представлена в виде набора непроницаемых кубов, разделенных щелями. Реальный пласт при этом может иметь блоки породы различной величины и формы, а также трещины различной ширины.
Модель трещиновато-пористого пласта. В реальном пласте, которому соответствует эта модель, содержатся промышленные запасы нефти как в трещинах, так и в блоках, пористых и проницаемых. Эта модель может быть представлена в виде набора кубов, разделенных трещинами. Фильтрация жидкостей и газов, насыщающих трещиновато-пористый пласт, происходит как по трещинам, так и по блокам. При этом вследствие значительной проницаемости трещин по сравнению с проницаемостью блоков любые изменения давления распространяются по трещинам быстрее, чем по блокам, в результате чего для разработки трещиновато-пористых пластов характерны перетоки жидкостей и газов из блоков в трещины и наоборот.
Жесткий водонапорный режим
Режимы нефтяных пластов классифицируются по характеру сил, приво-
дящих в движение нефть.
В процессе разработки нефтяных месторождений при вытеснении нефти
водой приходится иметь дело с фильтрацией упругой жидкости в упругой по-
ристой среде, причем, строго говоря, всегда с неустановившейся фильтрацией.
Однако благодаря тому, что разработка нефтяной залежи – сравнительно медленный процесс, при решении некоторых фильтрационных задач упругостью
жидкости и пористой среды можно пренебречь. Достаточно считать, что дви-
жение жидкости к зоне отбора осуществляется за счет напора контурных вод и
(или) напора закачиваемой воды. В таких случаях режим пласта считается же-
стким водонапорным. Основными условиями его существования являются: а)
наличие напора контурных вод и закачка в пласт необходимых объемов воды;
б) равенство количеств отобранной жидкости (нефти и воды) и вторгшейся в
пласт воды, иными словами – баланс отбора и закачки; в) пластовое давление
выше давления насыщения нефти газом.
При жестком водонапорном режиме связь между отборами жидкости и
перепадами давления не зависит от времени. Необходимо знать лишь гранич-
ные условия и параметры пласта и жидкостей в любой точке области фильтра-
ции (распределение по координатам).
4. Закон Дарси для совместной плоскорадиальной фильтрации нефти и воды
В случае совместной плоскорадиальной фильтрации нефти и воды закон Дарси записывается в следующем виде:
(1)
где 
— вектор скорости фильтрации нефти; 
— вектор скорости фильтрации воды; К — абсолютная проницаемость породы пласта; Kн(S), Kв(S) — относительные проницаемости соответственно для нефти и воды, зависящие от водонасыщенности S; mн, mв— коэффициенты динамических вязкостей нефти и воды; Рн, Рв — давления в нефти и воде, различием которых в дальнейших рассуждениях пренебрегают.
Рис. 1
В точке S=Sсв ОФП для воды равна нулю, так что Кв (S св )=0. Вода, первоначально содержащаяся в пористой среде вместе с нефтью, занимает преимущественно углы между зернами породы, тупиковые поры или обволакивает в виде пленки поверхность зерен породы. Это – неподвижная, «связанная» вода.
В точке S=S* ОФП для нефти равна нулю, так что Кн (S*)=0. Нефть,
имеющаяся в пласте при S= S*, может находиться в виде пленки на твердой по-
верхности пористой среды или глобул, занимающих тупиковые поры и углы
между зернами породы. Это – остаточная нефть, которая не может быть вытес-
нена из пласта даже при его бесконечной промывке.
С увеличением водонасыщенности проницаемость пласта для нефти в
каждом сечении снижается, а для воды – возрастает.
По форме кривых отчетливо видно, что порода имеет гидрофобный характер, т.к. точка пересечения кривых ОФП расположена левее значения S=0,5.
Истинное; 3 — фиктивное
Распределение водонасыщенности в пласте изменяется по мере продви-
жения фронта вытеснения таким образом, что значения Sв на фронте вытеснения rв и S* на входе в пласт остаются неизменными. При этом, как видно из рис.2, кривая распределения водонасыщенности словно «растягивается», оставаясь подобной самой себе. Такое распределение любого параметра, как и соответст-
вующее решение задачи, называется автомодельным.
Для определения технологических показателей разработки кругового
пласта при t>t* поступают следующим образом. Считают, что продвижение
фронта вытеснения 1 на рис.2 происходит и в водный период разработки пла-
ста, но этот фронт распространяется вправо за пределы пласта (линия 3). Водо-
насыщенность на фиктивном фронте вытеснения rвф и в этом случае остается
постоянной, равной Sв , а водонасыщенность при r=rк будет увеличиваться, со-
ставляя S .
11. Отличие друг от друга водного и безводного периодов разработки
Безводный период разработки продолжается до тех пор, пока вода не достигнет внешней границы пласта rк, в течение этого периода будет извлекаться безводная продукция, т.е. чистая нефть. После достижения водой rк наступает период добычи обводненной продукции, т.е. будет извлекаться не чистая нефть, как в случае безводного периода, а нефть вместе с водой. Со временем обводненность продукции может расти, достигая 98,5%, при обводненности продукции выше этого значения, добыча не рентабельна по экономическим соображениям.
Накопленная добыча нефти
Накопленная добыча нефти отражает количество нефти, добытое по объекту за определенный период времени с начала разработки, т. е. с момента пуска первой добывающей скважины.
13. Расчет прогнозной обводненности и определение фактической
Для определения прогнозной обводненности продукции ν используют
выражение
ƒ(S) = 
= 
= 
(6)
Таким образом, расчетная обводненность продукции приравнивается к
функции Бакли-Леверетта. Фактическую обводненность продукции можно будет определить лишь в процессе добычи жидкости из скважины, по количеству воды, приходящейся на единицу добываемой нефти.
14. Как рассчитать перепад давления в элементе системы разработки, пользуясь методом эквивалентных фильтрационных сопротивлений? Какая модель вытеснения при этом используется?
Для расчета перепада давления таким образом элемент системы разработки представляют в виде круга, в центре которого располагается нагнетательная скважина. 
Движение жидкостей считают плоскорадиальным. Радиус rк определяют из условия равенства площадей исходного семиточечного и эквивалентного ему кругового элемента. Рассматривая характер течения жидкостей, приближенно разделяют фильтрационные сопротивления на две части — внешние, возникающие в круговой области при rнс £ r £ R, и внутренние, находящиеся вблизи добывающих скважин при s /p ³ r³ rс.
В какой-то момент времени вода внедряется в пласт на расстояние rв от нагнетательной скважины. Если считать характер вытеснения поршневым, то течение в рассматриваемом элементе складывается из трех: 1) радиального (течение воды) от нагнетательной скважины до границы раздела воды с нефтью, rнс £ r £ rв; 2) радиального (течение нефти) от границы раздела с водой до условного контура радиуса R,
Перепады давления на границах выделенных таким способом областей запишутся в следующем виде:
| |
| |
|
где Рв — давление на границе раздела нефти и воды; PR — давление на условном контуре радиусом R.
Последнее выражение написано с учетом того, что при семиточечной схеме расположения скважин в случае жесткого водонапорного режима q=2qc.
Соотношение нагнетательных и добывающих скважин для семиточечной системы составляет 1:2. Четыре добывающие скважины входят в состав смежных элементов. Поэтому единичный семиточечный элемент площади содержит одну нагнетательную и две добывающие скважины.
Сложив перепады давления на границах выделенных областей, получим выражения для определения DP:
|
В таком виде формула пригодна для определения перепада давления в случае поршневого вытеснения нефти водой.
Рис.4. Несовершенная скважина по степени вскрытия пласта
2) Если скважина вскрывает пласт до подошвы, но сообщение с пластом происходит только через специальные отверстия в обсадной колонне и цементном камне или через специальные фильтры, то такую скважину называют гидродинамически несовершенной по характеру вскрытия пласта;
Рис.5. Несовершенная скважина по характеру вскрытия пласта
3) С двойным видом несовершенства — как по степени, так и по характеру вскрытия пласта;
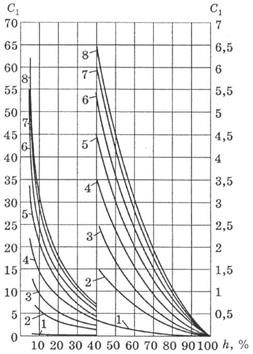
4) По качеству вскрытия. С = С1 + С2 — дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия пласта С1 и характеру вскрытия С2. Где С1 определяется по графику зависимости величины С1 от параметров а = h/Dс и 
= b/h; и величины С2 — от трех параметров: nDc, l = l¢/Dc, a = d0 /Dc, где n -число перфорационных отверстий на один метр вскрытой толщины пласта; Dс — диаметр скважины; l’ — глубина проникновения пуль в породу; d0-диаметр отверстий. Такие исследования были проведены В. И. Щуровым.
Рис. 6. Рис. 7.
Графики Щурова
ЗАДАНИЕ
Нефтяное месторождение площадью F запланировано разрабатывать с использованием заводнения при площадной семиточечной схеме размещения скважин.
Месторождение вводится в эксплуатацию и обустраивается за Т лет, причем равномерно за каждые 0,5 года вводится в разработку N элементов площади (один элемент включает одну нагнетательную и шесть добывающих скважин). Основной объект разработки месторождения — нефтенасыщенный пласт, сложенный терригенными коллекторами, который имеет следующие параметры: общая нефтенасыщенная толщина h0, абсолютная проницаемость К, пористость m, насыщенность связанной водой Sсв, вязкость нефти в пластовых условиях µн, вязкость пластовой и закачиваемой воды µв.
Результаты геофизических исследований позволяют утверждать, что пласт в пределах нефтенасыщенной площади однороден по проницаемости.
Математическая обработка данных лабораторных экспериментов по вытеснению нефти водой показала, что зависимости относительных фазовых проницаемостей для нефти Кн(S) и воды Кв(S) от водонасыщенности S представляются в виде аналитических соотношений:
При этом Sсв и S* известны. Значение S1 определяется из условия равенства относительных проницаемостей для нефти и воды при S=S1.
В соответствии с проектом разработки в каждую нагнетательную скважину радиусом rнс= 0,1 м закачивается вода с расходом q. Коэффициент охвата пласта заводнением принят по проекту равным Ƞ2.
Добывающие скважины выбывают из эксплуатации при обводненности продукции, равной В.
Т р е б у е т с я:
1) определить изменение во времени добычи нефти, воды, обводненности
продукции и текущей нефтеотдачи для элемента системы разработки и для месторождения в целом;
2) рассчитать динамику среднесуточных дебитов жидкости, нефти и воды
для одной добывающей скважины;
3) определить перепад давления в элементе системы разработки при rв=rнс, rв= rк /2 и rв=rк, если приведенный радиус добывающей скважины rс =0,01м.
РАСЧЕТНАЯ ЧАСТЬ
Исходные данные
площадь месторождения F= 1980⋅10 4 м 2 ;
нефтенасыщенная толщина пласта h0=12 м;
коэффициент пористости m= 0,23;
абсолютная проницаемость К= 0,5 мкм 2 ;
насыщенность связанной водой Sсв= 0,07;
предельная водонасыщенность S * = 0,8;
динамическая вязкость нефти µн= 2 мПа⋅с;
динамическая вязкость воды µв= 1 мПа⋅с;
расход закачиваемой воды q= 500 м 3 /сут;
коэффициент охвата заводнением Ƞ2= 0,74;
время ввода в разработку Т= 2 года;
число элементов площади,
вводимых в эксплуатацию в течение
полугода N=18 ед.;
предельная обводненность В=99 %.
Последовательность расчёта
1. Определение численных значений коэффициента А и параметра S1, входящих в приведенные зависимости Kн(S) и Kв(S).
Значение коэффициента А находим из условия, что Kв(1)=1.
.
Значение параметра S1 установим из условия:
.
2. Определим относительные проницаемости нефти и воды в зависимости от водонасыщенности.
Зададимся значениями S от Sсв до 1 и произведём расчеты по формулам (11), (12) и (13), строим график (рис.8), данные расчета заносим в таблицу 1.
| S | Kн | Kв |
| 0,07 | 1,00 | 0,00 |
| 0,10 | 0,92 | 0,00 |
| 0,13 | 0,84 | 0,01 |
| 0,16 | 0,77 | 0,02 |
| 0,19 | 0,70 | 0,03 |
| 0,22 | 0,63 | 0,04 |
| 0,25 | 0,57 | 0,06 |
| 0,28 | 0,51 | 0,08 |
| 0,31 | 0,45 | 0,11 |
| 0,34 | 0,40 | 0,14 |
| 0,37 | 0,35 | 0,17 |
| 0,40 | 0,30 | 0,20 |
| 0,43 | 0,26 | 0,24 |
| 0,46 | 0,22 | 0,29 |
| 0,49 | 0,18 | 0,33 |
| 0,52 | 0,15 | 0,38 |
| 0,55 | 0,12 | 0,43 |
| 0,58 | 0,09 | 0,49 |
| 0,61 | 0,07 | 0,55 |
| 0,64 | 0,05 | 0,61 |
| 0,67 | 0,03 | 0,68 |
| 0,70 | 0,02 | 0,74 |
| 0,73 | 0,01 | 0,82 |
| 0,76 | 0,003 | 0,86 |
| 0,79 | 0,0002 | 0,88 |
| 0,80 | 0,0000 | 0,89 |
| 0,82 | 0,90 | |
| 0,85 | 0,92 | |
| 0,88 | 0,93 | |
| 0,91 | 0,95 | |
| 0,94 | 0,97 | |
| 0,97 | 0,98 | |
| 1,00 | 1,00 |
Данные расчета ОФП
Рис. 8. Зависимость относительных проницаемостей для нефти
Рис. 9. График функции Бакли-Леверетта
Провели касательную к кривой f(S) из точки S=Sсви определили значение водонасыщенности на фронте вытеснения нефти водой Sв=0,48, а также f(Sв)=0,755.
4. Построили и обработали график производной функции Бакли-Леверетта. Функцию f’(S) получили, дифференцируя функцию f(S). Полученные данные записываем в таблицу 3. Строим график функции f’(S) зависимости от S (рис.10).
При 
При 
|
При S=S * =0,74 
| S | f'(S) |
| 0,07 | 0,00 |
| 0,1 | 0,25 |
| 0,13 | 0,56 |
| 0,16 | 0,93 |
| 0,19 | 1,33 |
| 0,22 | 1,75 |
| 0,25 | 2,14 |
| 0,28 | 2,48 |
| 0,31 | 2,72 |
| 0,34 | 2,84 |
| 0,37 | 2,83 |
| 0,4 | 2,70 |
| 0,43 | 2,48 |
| 0,46 | 2,20 |
| 0,49 | 1,89 |
| 0,52 | 1,57 |
| 0,55 | 1,28 |
| 0,58 | 1,01 |
| 0,61 | 0,78 |
| 0,64 | 0,58 |
| 0,67 | 0,42 |
| 0,7 | 0,28 |
| 0,73 | 0,18 |
| 0,743 | 0,13 |
| 0,75 | 0,11 |
| 0,76 | 0,09 |
| 0,79 | 0,02 |
| 0,8 | 0,00 |
Рис. 10. График производной функции Бакли-Леверетта
С учетом того, что Sв = 0,48, найдем f’(Sв)=1,89, рассчитанное с помощью соотношения:
5. Определим длительность безводного периода добычи нефти из элемента площади, включающего семь скважин — одну нагнетательную и шесть добывающих . t *
где Vп– объем пор пласта, охваченных заводнением; h – охваченная заводнением толщина пласта, h=h0⋅h2; rк– кругового элемента, эквивалентного семиточечному элементу площади, рассчитывается по формуле
Площадь кругового элемента Fэопределяют, зная общую площадь месторождения, а также сроки и темпы его ввода в эксплуатацию. Для заданных условий
6. Рассчитаем технологические показатели разработки элемента: обводненность продукции, суточную добычу нефти и воды, текущую и накопленную добычу нефти, коэффициент текущей нефтеотдачи.
До тех пор, пока фронт вытеснения нефти водой не дойдет до внешней границы элемента r=rк, из пласта будет добываться чистая нефть в количестве, равном объему закачиваемой воды. Обводненность продукции будет равна нулю.
В момент времени t=t * , когда фронт вытеснения подойдет к границе элемента rк, начнется вторая стадия разработки элемента – стадия добычи обводненной продукции. Для определения технологических показателей элемента при t>t * предположили, что фронт вытеснения нефти водой существует как фиктивный, т.е. кажущийся фронт вытеснения при r>rк. Обозначаем водонасыщенность на границе элемента r=rк через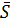 
. Используя изложенное предположение, получили следующие очевидные соотношения для моментов времени t>t * :
Данное соотношение служит для определения 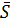. С этой целью задаемся различными значениями t и, зная t * и f'(Sв), рассчитываем значения f’ 
Далее по графику (рис.10) находим значения водонасыщенности .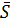
По найденным значениям 
помощью рис.9 или соответствующих расчетных зависимостей определяем значения f(S). Таким образом, находят обводненность добываемой в момент времени t продукции vэ, поскольку vэ=f(S).
Суточная добыча нефти из элемента qнэ, приведенная к пластовым условиям, при t>t * составляет
суточная добыча воды
Текущую добычу нефти ∆Qнэ за период продолжительностью полгода или год определяют, умножая суточную добычу нефти на 182,5 или 365 сут. Поскольку на стадии добычи обводненной продукции суточные отборы нефти непрерывно снижаются, в расчете используем их среднее арифметическое значение на начало и конец каждого периода.
Накопленную добычу нефти Qнэ находим суммированием текущих отборов нефти.
Текущую нефтеотдачу ηэ для элемента разработки определяем следующим образом:
Видно, что дальнейшие вычисления связаны с интегрированием (графическим или численным) функции qнэ(t), что создает неудобство при расчете.
Решение можно получить проще, если учесть, что
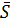
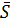
Результаты расчета параметров f'( ), , vэ, qнэ,, qвэ, ∆Qнэ, Qнэ и ηэ для заданных значений времени t заносим в табл.4.
Сравнение показателей
| Показатель | t * =1,628 года | t * =3,2562 года | |
| Коэффициент нефтеотдачи | Для элемента | 0,516 | 0,521 |
| По месторождению | 0,499 | 0,520 | |
| Время разработки, лет | |||
| Количество добывающих скважин | |||
| Добыча нефти на конец разработки, тыс. м 3 | 25,37931 | 26,43662 | |
| Добыча воды на конец разработки, тыс. м 3 | 99,45069 | 66,91457 |
Получим, что КИН для элемента изменён, но не значительно. Но КИН по всему месторождению выше для 2-го случая (уменьшения время ввода в эксплуатацию Т в 2 раза). Дополнительная добыча составит 1,05731 тыс. м 3 нефти. При уменьшении Т в 2 раза значительно уменьшается фонд скважин (на 108), при этом коэффициент охвата пласта остается неизменным, что приводит к значительному уменьшению закачки воды в пласт при еще большей добыче нефти, несмотря на то, что сильно увеличилось время разработки месторождения.
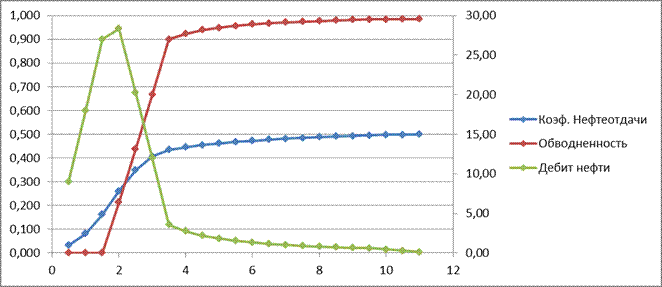
Графики основных показателей разработки для двух случаев приведены на рисунках 15 и 16.
ВЫВОД
При увеличении продолжительности безводной добычи нефти в 2 раза, увеличивается и время разработки месторождения, что приводит к дополнительным затратам. Но при этом уменьшается количество вводимых в эксплуатацию добываемых и нагнетальных скважин. В плане нефтеотдачи только изменение времени ввода в эксплуатацию элементов повлияло на конечный КИН (увеличение составило 4%). Поэтому, после всего вышеизложенного увеличение безводного периода добычи нефти, несомненно, доказывает свою полезность.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Басниев К.С., Дмитриев Н.М., Каневская Р.Д., Максимов В.М. Подземная гидромеханика: Учеб. для вузов. — М.-Ижевск: Институт компьютерных исследований, 2005.-496 с.
2. Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика: Учеб. для вузов. — М.: Недра, 1993. — 416 с.
3. Желтов Ю.П. Разработка нефтяных месторождений: Учеб. для вузов. — М.: ОАО «Издательство «Недра», 1998. — 365 с.
4. Щуров В.И. Технология и техника добычи нефти: Учеб. для вузов. – М.:ООО ТИД «Альянс», 2005. – 510 с.
5. Подземная гидромеханика: Учеб. пособие. / В.А.Ольховская; Самар. гос. техн. ун-т: Самара, 2007. — 177 с.
6. Использование моделей пониженной размерности в прикладных задачах подземной гидромеханики: Учеб. пособие / В.А.Ольховская. — Самара: Самар. гос. техн. ун-т, 2011. — 105 с.
7. Гиматудинов Ш.К. Физика нефтяного и газового пласта: Учебник –
М.: Недра, 1971. – 312 с.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Модель непоршневого вытеснения нефти
Модель непоршневого вытеснения нефти водой – это гидродинамическая
модель процесса заводнения, основанная на теории совместной фильтрации не-
однородных несмешивающихся жидкостей.
Первое решение задачи двухфазной фильтрации было получено амери-
канскими исследователями Бакли и Левереттом для двух несмешивающихся
несжимаемых жидкостей при пренебрежении гравитационными и капиллярны-
Для большинства пластов при вытеснении из них нефти водой характерно
возникновение в порах раздробленных (диспергированных) глобул нефти. Если
в единице объема пористой среды содержится сравнительно небольшое число
тупиковых зон, то нефть будет продолжать двигаться позади фронта вытесне-
ния вместе с водой и извлекаться из пласта по мере его заводнения. Таким об-
разом, вода не заполняет полностью область, первоначально занятую нефтью. В
этой области происходит совместное движение двух жидкостей – вторгшейся
воды и оставшейся, постепенно вымываемой нефти.
В отличие от модели поршневого вытеснения, согласно которой из об-
воднившихся пропластков нефть не извлекается, модель непоршневого вытес-
нения учитывает совместную (двухфазную) фильтрацию нефти и воды в порис-
той среде. При этом водонасыщенность в каждом сечении заводненной области
непрерывно увеличивается, достигая предельного значения S*.
Модель процесса непоршневого вытеснения нефти водой позволяет дос-
таточно точно рассчитывать показатели разработки пласта в период добычи об-
водненной продукции даже в сочетании с моделью однородного пласта. В ее
основе лежат зависимости относительных фазовых проницаемостей для нефти
и воды от водонасыщенности S.
Типы моделей пластов
Модели пластов условно подразделяют на детерминированные и вероятностно-статистические.
Детерминированные модели – это такие модели, в которых стремятся воспроизвести как можно точнее фактическое строение и свойства пластов, как бы создавая «фотографию» пласта. При расчете процессов разработки месторождения с использованием детерминированной модели всю площадь пласта или его объем разбивают на определенное число ячеек и каждой ячейке придают те свойства, которые присущи пласту в области ее расположения. Дифференциальные уравнения разработки месторождения заменяют конечно-разностными соотношениями, а затем производят расчет с помощью вычисли-
Вероятностно-статистические модели не отражают детальные особенно-
сти строения и свойства пластов, но количественно характеризуют их главные
особенности. К числу наиболее известных вероятностно-статистических моде-
лей пластов относятся модели однородного, слоистого, трещиноватого и тре-
В модели однородного пласта основные параметры реального пласта
(пористость, проницаемость), изменяющиеся от точки к точке, осредняют. Час-
то, используя модель такого пласта, принимают гипотезу и о его изотропности,
т.е. о равенстве проницаемостей в любом направлении, исходящем из рассмат-
риваемой точки пласта. Однако иногда пласт считают анизотропным. При этом
принимают, что проницаемость пласта по вертикали (главным образом, вслед-
ствие напластования) отличается от его проницаемости по горизонтали.
Модель слоистого пласта представляет собой структуру (пласт), состоящую из набора слоев с пористостью и проницаемостью. При всем этом считают, что из всей толщины пласта слои с пористостью и проницаемостью составляют часть и т.д.
Модель трещиноватого пласта. Если нефть в пласте залегает в трещинах, разделяющих непористые и непроницаемые блоки породы, то модель такого пласта может быть представлена в виде набора непроницаемых кубов, разделенных щелями. Реальный пласт при этом может иметь блоки породы различной величины и формы, а также трещины различной ширины.
Модель трещиновато-пористого пласта. В реальном пласте, которому соответствует эта модель, содержатся промышленные запасы нефти как в трещинах, так и в блоках, пористых и проницаемых. Эта модель может быть представлена в виде набора кубов, разделенных трещинами. Фильтрация жидкостей и газов, насыщающих трещиновато-пористый пласт, происходит как по трещинам, так и по блокам. При этом вследствие значительной проницаемости трещин по сравнению с проницаемостью блоков любые изменения давления распространяются по трещинам быстрее, чем по блокам, в результате чего для разработки трещиновато-пористых пластов характерны перетоки жидкостей и газов из блоков в трещины и наоборот.
Жесткий водонапорный режим
Режимы нефтяных пластов классифицируются по характеру сил, приво-
дящих в движение нефть.
В процессе разработки нефтяных месторождений при вытеснении нефти
водой приходится иметь дело с фильтрацией упругой жидкости в упругой по-
ристой среде, причем, строго говоря, всегда с неустановившейся фильтрацией.
Однако благодаря тому, что разработка нефтяной залежи – сравнительно медленный процесс, при решении некоторых фильтрационных задач упругостью
жидкости и пористой среды можно пренебречь. Достаточно считать, что дви-
жение жидкости к зоне отбора осуществляется за счет напора контурных вод и
(или) напора закачиваемой воды. В таких случаях режим пласта считается же-
стким водонапорным. Основными условиями его существования являются: а)
наличие напора контурных вод и закачка в пласт необходимых объемов воды;
б) равенство количеств отобранной жидкости (нефти и воды) и вторгшейся в
пласт воды, иными словами – баланс отбора и закачки; в) пластовое давление
выше давления насыщения нефти газом.
При жестком водонапорном режиме связь между отборами жидкости и
перепадами давления не зависит от времени. Необходимо знать лишь гранич-
ные условия и параметры пласта и жидкостей в любой точке области фильтра-
ции (распределение по координатам).
4. Закон Дарси для совместной плоскорадиальной фильтрации нефти и воды
В случае совместной плоскорадиальной фильтрации нефти и воды закон Дарси записывается в следующем виде:
(1)
где — вектор скорости фильтрации нефти;
Источник
