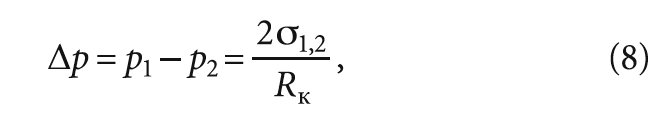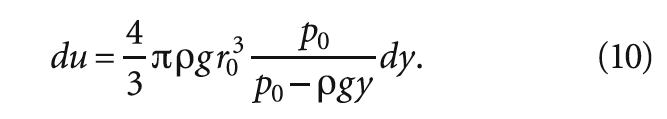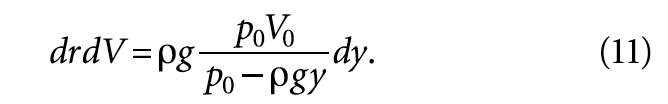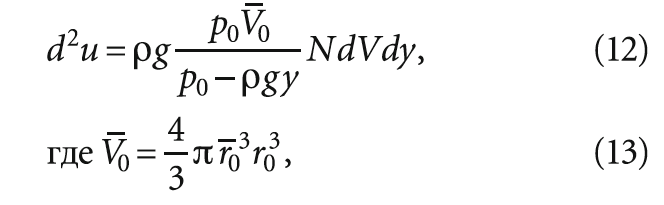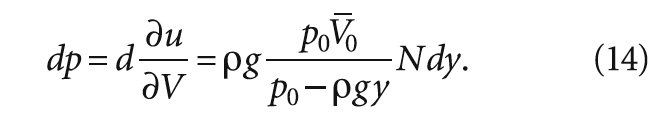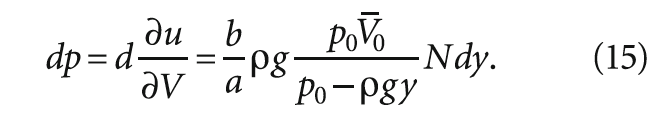Пузырьки воздуха под водой

Содержание

Звуки пузырей в воде скачать и слушать онлайн
Обнаружен эффект памяти в поведении пузырьков воздуха под водой
Теоретические исследования движения пузырьков воздуха в потоке воды при аэрации

Звуки пузырей в воде скачать и слушать онлайн

[76,12 Kb] (cкачиваний: 989). Тип файла: mp3.

Звук, где человек под водой создает пузырьки

[147,14 Kb] (cкачиваний: 346). Тип файла: mp3.

Звук, где человек ртом создают пузыри из воды, он дует в воду

[87,55 Kb] (cкачиваний: 123). Тип файла: mp3.

Звук бульканья воды

[25,92 Kb] (cкачиваний: 121). Тип файла: mp3.

Водные воздушные пузыри

[26,33 Kb] (cкачиваний: 88). Тип файла: mp3.

Звук: маленькие пузырьки поднимаются вверх по воде

[38,98 Kb] (cкачиваний: 707). Тип файла: mp3.

Звук воздуха, который идет через воду, создавая пузыри

[63,47 Kb] (cкачиваний: 228). Тип файла: mp3.

Один пузырь, который поднялся в воздух

[10 Kb] (cкачиваний: 358). Тип файла: mp3.

[16,12 Kb] (cкачиваний: 205). Тип файла: mp3.

Звук пузырей в бассейне

[15,3 Kb] (cкачиваний: 117). Тип файла: mp3.

Один средний пузырь

[11,02 Kb] (cкачиваний: 129). Тип файла: mp3.

[12,04 Kb] (cкачиваний: 71). Тип файла: mp3.

Звук всплытия человека из воды с пузырем

[60,2 Kb] (cкачиваний: 67). Тип файла: mp3.

Это добавим для разнообразия

[237,55 Kb] (cкачиваний: 145). Тип файла: mp3.

Звук пузырей из трубочки

[78,16 Kb] (cкачиваний: 126). Тип файла: mp3.

[140 Kb] (cкачиваний: 73). Тип файла: mp3.

Пузыри под водой

[235,71 Kb] (cкачиваний: 163). Тип файла: mp3.

Вода брызгает от пузырей

[264,69 Kb] (cкачиваний: 57). Тип файла: mp3.

[168,77 Kb] (cкачиваний: 253). Тип файла: mp3.

Если вам этого оказалось мало, то слушайте ещё звуки пузырьков.

Источник

Обнаружен эффект памяти в поведении пузырьков воздуха под водой

Открыто новое явление в гидродинамике: эффект памяти формы при отрыве от поверхности пузырьков воздуха под водой. Гидродинамические течения, движимые сингулярностями, но обладающие памятью, встречаются физикам впервые.

Рис. 1. За мгновение до отрыва пузырька воздуха под водой от поверхности возникает перешеек, который утончается до атомных размеров. Однако чтобы это наблюдать, необходима строгая симметрия и абсолютно вертикальная ориентация выходного отверстия (изображение из статьи Phys. Rev. Lett. 97, 144503)

Капли воды, просачивающиеся через плохо закрытый кран, получаются круглыми вне зависимости от того, было ли выходное отверстие круглое, треугольное или же имело какую-то более сложную форму. Это неудивительно, поскольку поверхностное натяжение и вязкость как раз стремятся превратить любую исходную форму в круглую. Можно сказать, что под действием этих сил вода «забывает» свое начальное состояние.

В процессе образования капли есть, однако, один интригующий этап, детали которого до сих пор не до конца изучены. За считанные мгновения до отрыва капли её основная масса уже движется вниз под действием силы тяжести, а с исходной поверхностью её соединяет лишь узкий перешеек. При приближении к моменту отрыва этот перешеек вытягивается и утончается до атомных размеров и наконец рвется.

Рис. 2. Отрыв пузырька при слегка наклоненном выходном отверстии: вид спереди и сбоку. Даже слабое нарушение симметрии сказывается на форме перешейка (изображение из статьи Phys. Rev. Lett. 97, 144503)

Теоретические вычисления предсказывали, что процесс утончения перешейка тоже характеризуется потерей памяти о первоначальной форме. Не важно, каково было выходное отверстие: перешеек быстро принимал осесимметричную форму. Развитая в последние десятилетия прошлого века технология сверхскоростной видеосъемки (с частотой свыше 100 тысяч кадров в секунду) подтвердила в общих чертах правильность этого вывода.

Сам факт, что течения вязкой жидкости приводят к потере первоначальной формы, казался настолько естественным, что противоречащие ему экспериментальные результаты, полученные в 2003 году исследователями из Университета Чикаго и опубликованные в статье P. Doshi et al., Science, 302, 1185 (2003), были встречены физиками с нескрываемым удивлением. Оказалось, что при отрыве капли воды не в воздухе, а внутри другой, более вязкой жидкости, форма перешейка сильно зависит от формы отверстия, из которого просачивается вода. Напрашивался вывод, что более важную роль в этом процессе играет не сама та жидкость, которая «каплет», сколько среда, внутри которой это происходит.

Последние исследования этой же группы из Чикаго, описанные в статье N. C. Keim et al., Physical Review Letters, 97, 144503 (3 October 2006), доступной также как cond-mat/0605669, можно считать естественным продолжением этого открытия. В них экспериментально изучался отрыв пузырьков воздуха в воде — ситуация, в которой роль окружающей каплю среды сведена к минимуму.

Пузырьки воздуха получались в эксперименте с помощью погруженного в воду и направленного вверх шприца с различными насадками: круглой, овальной и насадкой с профилем в форме полумесяца. Вся установка располагалась на платформе, которую можно было при необходимости наклонять на требуемый угол. Поведение пузырьков фиксировалось на камеру «Phantom» version 7 , позволявшей получать до 130 000 снимков в секунду, и затем обрабатывалось компьютером.

Рис. 3. Насадка с сечением в форме полумесяца порождает очень несимметричные перешейки (изображение из статьи Phys. Rev. Lett. 97, 144503)

Авторы выяснили, что «классический» сценарий разрыва перешейка (строгая цилиндрическая симметрия и утончение до субмикронных размеров) реализуется только в очень специальных условиях: при строго круглой насадке и абсолютно вертикальной её ориентации. Достаточно взять насадку с чуть вытянутым профилем или же слегка — всего на пару градусов! — наклонить установку, как процесс преображается. Перешеек искажается в направлении вытянутости, принимает плоскую лентообразную форму вместо цилиндрической и затем резко разрывается.

Насадка с еще более несимметричным профилем — в форме полумесяца — производила пузырьки, которые соединялись с ней желобкообразными перешейками. Эта форма сохранялась на протяжении всего процесса утончения и, как показывают снимки, разрыв происходил сразу в нескольких местах.

Иными словами, форма перешейка, соединяющего каплю с поверхностью, повторяет форму выходного отверстия и сохраняется практически неизменной при сужении «перетяжки» в сотни раз! Значит, в этом случае гидродинамические течения не только не «стирают» память о первоначальной форме, но и тщательно её сохраняют. Гидродинамические течения со столь необычными свойствами физикам до сих пор не встречались.

Стоит отметить, что в этой истории физиков-теоретиков больше беспокоит не само по себе необычное поведение воды, а тот факт, что определенный математический прием, часто используемый в теоретической физике, на этот раз дал осечку. Речь идет о выделении доминирующей сингулярности при изучении поведения решений уравнений эволюции. Дифференциальные уравнения, описывающие эволюцию какой-либо системы во времени, могут быть очень сложными, но при приближении к «катастрофическому» моменту (в данном случае — к моменту разрыва перешейка) они, как правило , существенно упрощаются. Обычно удается выделить ту главную силу, которая толкает систему к катастрофе, а всё остальное при этом становится второстепенным. В этом случае поведение системы вблизи критического момента обычно ничего не «помнит» о начальных условиях просто потому, что главная сингулярность слишком проста, чтоб вобрать в себя эту информацию.

В данном случае эксперименты показали, что система ведет себя самоподобно — что характерно для систем, движимых какой-то одной главной сингулярностью, — но при этом информация о начальном состоянии сохраняется в течение всей эволюции. Что это за сингулярность, которая умудряется быть одновременно столь простой и столь информационно емкой, физикам и предстоит разобраться.

Не исключено, что эти, казалось бы, чисто математические тонкости вскоре отразятся и на прикладной физике или даже на современных технологиях. Образование и отрыв капелек и пузырьков используется повсеместно, начиная с химической промышленности и заканчивая струйными принтерами. Теоретическое моделирование таких процессов, которое предваряет их внедрение в технологии, до сих пор игнорировало саму возможность подобных эффектов памяти. Для физика же эта работа является лишним подтверждением того, что несмотря на многовековую историю гидродинамики, нестационарные течения со свободной поверхностью до сих пор таят в себе немало сюрпризов.

Источник

Теоретические исследования движения пузырьков воздуха в потоке воды при аэрации

УДК 628.16. Научная специальность: 05.23.04.

Теоретические исследования движения пузырьков воздуха в потоке воды при аэрации

В. Б. Викулина, к.т.н., доцент; Л. В. Инешина, студентка бакалавриата, Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ)

Аэрационные сооружения, используемые в очистке воды, требуют оптимизации технологического процесса по признакам формирования и распределения воздушных масс в потоке водоочистного сооружения. В качестве транспортного потока в водоочистных сооружениях используется вода, поэтому это обстоятельство позволяет использовать законы гидродинамики потока при всплытии пузырьков воздуха в качестве дополнительного фактора. В статье приводятся физические принципы всплытия пузырьков воздуха при аэрации. Теоретически обосновывается всплывание пузырьков воздуха в статических условиях жидкости и динамических условиях потока. Получена теоретическая зависимость, которая направлена на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.

Ключевые слова: аэрация, пузырёк воздуха, вязкость динамическая, скорость потока, граница раздела фаз, распределение скоростей.

UDC 628.16. The number of scientific speciality: 05.23.04.

Theoretical studies of the motion of air bubbles in the water flow during aeration

V. B. Vikulina, PhD, Associate Professor; L. V. Inesina, undergraduate student, Moscow State University of Civil Engineering (MGSU)

Aeration facilities used in water treatment require optimization of the technological process on the basis of the formation and distribution of air masses in the flow of the water treatment plant. Water is used as a transport flow in water treatment facilities, so this circumstance allows to use the laws of flow hydrodynamics at the ascent of air bubbles as an additional factor. Physical principles of air bubbles ascent during aeration are given. Theoretically justified the rise of air bubbles in static fluid conditions and dynamic flow conditions. The obtained theoretical dependence, which is aimed at the normalization of instability of operation of the aeration structures and the determination of optimal process conditions.

Keywords: aeration, air bubble, dynamic viscosity, flow rate, phase boundary, velocity distribution.

Движение потоков в сооружениях водоочистки с аэрацией (например, аэротенк, аэрофильтр, аэрируемая песколовка) создают технологическую особенность. Основным процессом, в физическом понимании аэрации, является движение пузырьков воздуха снизу вверх. Рассмотрим всплывание пузырька воздуха в жидкости, находящейся в состоянии покоя.

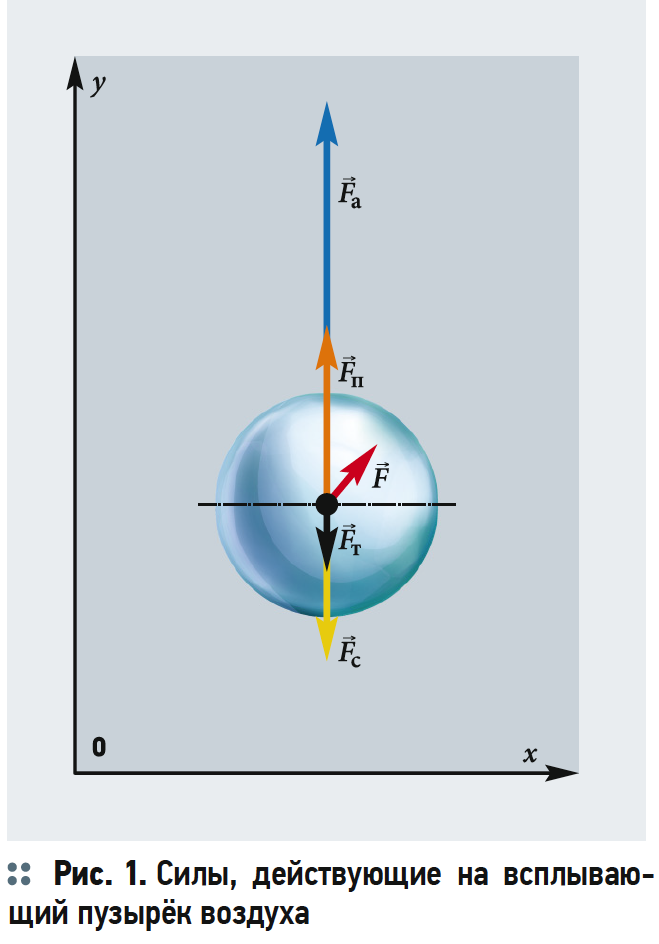
Предположим, что пузырёк воздуха в жидкости имеет форму шара [1].

На всплывающий пузырёк действуют три силы: сила тяжести F_т, архимедова сила F_а и сила сопротивления F_c (рис. 1). В проекции на вертикальную ось OY подъёмная сила F_п равна:

Силы выражаются в ньютонах (Н).

Рассмотрим действие сил при равномерном движении пузырька в воде.

Сила Архимеда (выталкивающая сила) приводит пузырёк в движение вверх, при этом диаметр пузырька увеличивается, достигая своего максимума на поверхности воды.

Сила Стокса (сила трения) при движении пузырька действует в направлении, противоположном силе Архимеда, и направлена сверху вниз.

Сила тяжести действует в условиях ускорения свободного падения и направлена сверху вниз.

Сила Стокса возникает в результате взаимодействия жидкости с пузырьком и равна силе трения, на преодоление которой затрачивается работа.

Разность энергий двух состояний пузырька до начала совершения работы и после — это работа как избыточная свободная энергия. С точки зрения гидростатики дополнительная потенциальная энергия равносильна динамическому напору.

При условии сжимаемости воздуха и при движении пузырька вверх наружное давление на стенки пузырька будет меняться с высотой, а диаметр пузырька будет увеличиваться. Расширение воздуха в пузырьке может происходить либо изотермически, либо адиабатически. Поскольку размер пузырька определяют условия гидростатики и силы Стокса, то принимаем расширение воздуха в пузырьке как изотермическое, поэтому размеры пузырька должны быть достаточно малыми.

Запишем условие для изотермического процесса при вертикальном всплытии пузырька воздуха:

где p — давление жидкости, Па; V — объём жидкости, м³.

Если p₀ — атмосферное давление [Па], то давление на глубине h [м] в жидкости плотностью ρ [кг/м³] будет равно (p₀ + ρgh), где g — ускорение свободного падения, g = 9,81 м/с2; ρ — плотность жидкости, кг/м³; h — глубина, м.

Согласно закону изотермического расширения пузырька (2) на глубине слоя жидкости найдём радиус пузырька:

где r₀ — радиус пузырька на поверхности воды, мм.

Пузырёк движется со скоростью v в жидкости, характеризуемой динамической вязкостью [Па·с]. Движение сферического пузырька в жидкости, которая рассматривается как непрерывная среда, и размеры которого (пузырька) значительно превышают размеры молекул среды, описывается уравнением Стокса для вязкого сопротивления:

где F_c — сила Стокса, Па; м — динамическая вязкость, Па·с или Н·с/м²; v — скорость всплытия пузырька, м/с.

Сила Архимеда F_а (подъёмная сила для пузырька) определяется из выражения

и она равна силе Стокса.

Сила тяжести равна:

где m — масса пузырька, кг.

Сила тяжести зависит от геометрических размеров пузырька. Эта сила крайне мала в сравнении с силами, действующими на пузырёк воздуха в воде, следовательно, значением силы тяжести можно пренебречь.

Скорость всплывания пузырька находится по уравнению:

От шарообразной формы переходим к изменению форм пузырька [2, 3].

Пузырёк находится в движении во время подъёма до поверхности воды. При этом пузырёк воздуха принимает шарообразную форму за счёт действия сил поверхностного натяжения.

Кроме того, изменение давлений сред (внутренней и внешней) пузырька приводит к деформации его поверхности, что способствует колебанию пузырька.

Применительно к единичному всплывающему пузырьку, на границе раздела фаз возникает разность давлений Δр, описываемая уравнением:

где р₁ и р₂ — давления двух фаз на глубине, Па; σ_1,2 — поверхностное натяжение на границе двух фаз, Н/м; R_к — радиус кривизны поверхности рассматриваемого пузырька, м.

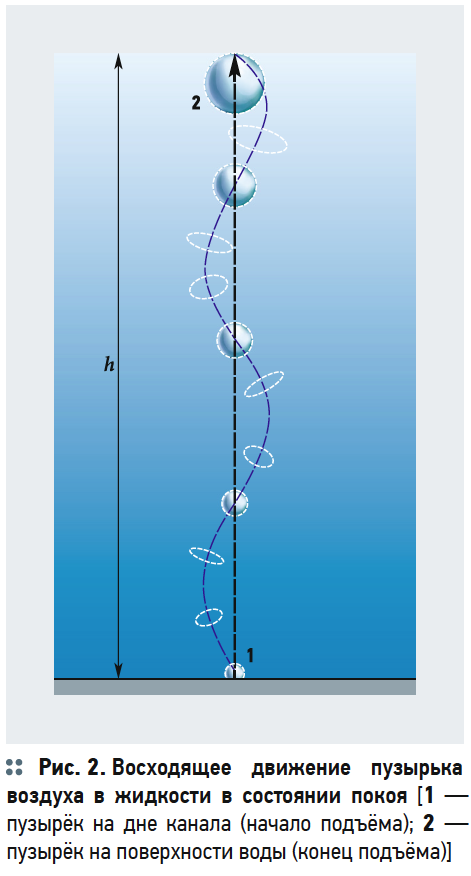
В результате увеличения объёма и изменения формы пузырька возникают его колебательные движения. Траектория всплытия пузырька принимается смещающейся относительно вертикали и носит волновой характер (рис. 2).

Теперь известны все величины, определяющие силу Стокса, что позволяет вычислить работу, совершаемую всплывающим пузырьком.

Вертикальное направление всплывания пузырька выберем за ось Oy.

Увеличение размеров и изменение формы пузырька передаётся окружающей пузырёк жидкости. Тем самым возникает суммарная работа dA и приращение свободной энергии согласно силам, действующим на пузырёк (рис. 1).

Поэтому приращение свободной энергии du в пересчёте на один пузырёк определится равенством:

где du и dA выражаются в джоулях (Дж).

Используя в формуле (9) выражения для силы Стокса (4), радиуса пузырька (3) и скорости всплытия пузырька (7), получаем следующий результат:

Для расчёта свободной энергии пузырьков введём функцию распределения f (r), которая представляет собой плотность вероятности обнаружения размера пузырька в единичном объёме между пузырьками с радиусами r и (r + dr).

Количество пузырьков с такими размерами в объёме dV будет равно f (r)drdV, поэтому их вклад в свободную энергию запишется как:

Помня, что V₀ = 4/3(πr₀ 3 ), и интегрируя по всем возможным размерам пузырьков, получаем:

здесь r_ 03 — среднее значение куба радиуса пузырька на уровне поверхности жидкости, мм³; количество пузырьков в единице объёма жидкости, шт.

Термодинамическая связь параметров системы определяет давление р в системе как производную свободной энергии по объёму. Избыточное давления жидкости тогда составит:

Рассмотрим всплытие пузырька воздуха в потоке жидкости при ламинарном режиме течения.

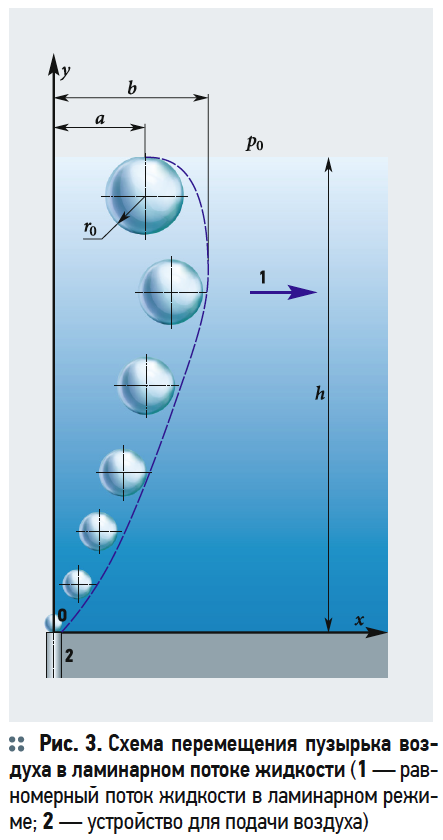
На рис. 3 представлена схема воздействие потока жидкости на вертикальное всплывание пузырька воздуха. Под воздействием распределения скоростей потока v = f(h) происходит смещение пузырька от вертикальной оси Oy. Согласно основным законам гидродинамики распределение скоростей зависит от кинетической энергии потока [3, 4]. По сечению потока происходит распределение скоростей, которые зависят от сопротивления между слоями жидкости при движении.

Нижние слои потока имеют сопротивление движению за счёт шероховатости дна, а движение верхнего слоя замедляется на границе раздела фаз «вода-воздух».

Обозначим через a [мм] расстояние от оси Oy до всплывшего пузырька на поверхности жидкости, а через b [мм] расстояние от оси Oy до всплывающего пузырька, максимально сместившегося по направлению движения жидкости.

Разница между a и b всплывающего пузырька зависит от скорости потока. Тогда выражение (14) запишется как

Полученная математическая зависимость позволяет более точно осуществить численные эксперименты на определённом этапе проектирования аэрационных сооружений систем водоочистки.

Эти действия направлены на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.

Выводы

1. Произведён анализ воздействия физических факторов на движение пузырька воздуха в воде, основанный на изотермическом процессе.

2. Получено уравнение, в котором приводится термодинамическая связь в определении давления в системе, как производная свободной энергии в потоке воды с учётом гидродинамических отклонений.

3. Использование полученного выражения позволяет повысить эффективность процесса водоочистки с применением аэрации.

Источник