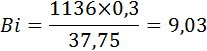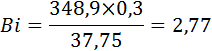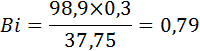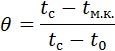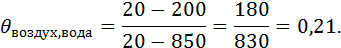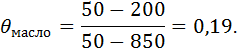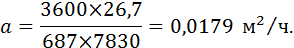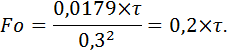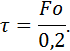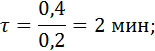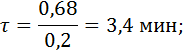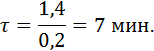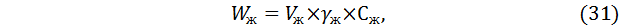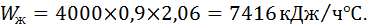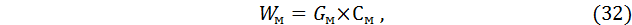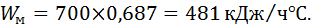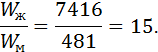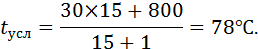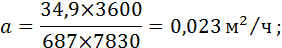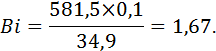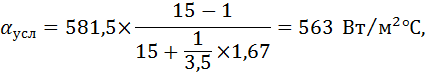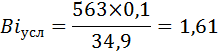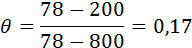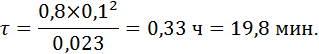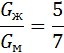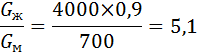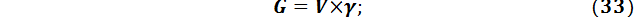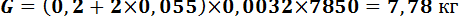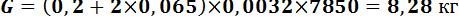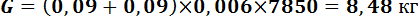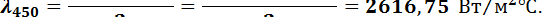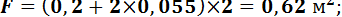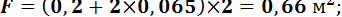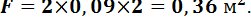Расчет охлаждения металла водой

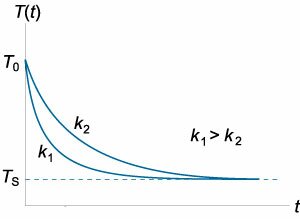
В конце \(17\) века британский ученый Исаак Ньютон изучал охлаждение тел. Эксперименты показали, что скорость охлаждения примерно пропорциональна разнице температур между нагретым телом и окружающей средой. Этот факт можно записать в виде дифференциального уравнения: \[\frac<><

> = \alpha A\left( <— T> \right),\] где \(Q\) − количество теплоты, \(A\) − площадь поверхности тела, через которую передается тепло, \(T\) − температура тела, \(<>\) − температура окружающей среды, \(\alpha\) − коэффициент теплопередачи , зависящий от геометрии тела, состояния поверхности, режима теплопередачи и других факторов.

Поскольку \(Q = CT,\) где \(C\) − теплоемкость тела, то дифференциальное уравнение можно записать как \[\frac<

> = \frac<<\alpha A>>\left( <— T> \right) = k\left( <— T> \right).\] Решение данного уравнение имеет вид: \[T\left( t \right) = + \left( <— > \right)>,\] где \(\) обозначает начальную температуру тела.

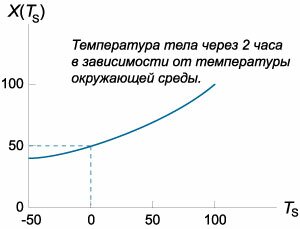
Таким образом, температура тела уменьшается экспоненциально по мере охлаждения, приближаясь к температуре окружающей среды. Скорость охлаждения зависит от параметра \(k = \large\frac<<\alpha A>>\normalsize\) ( коэффициента теплопроводности ). С увеличением коэффициента \(k\) (например, вследствие увеличения площади поверхности), тело будет охлаждаться быстрее (рисунок \(1\).)

Мы решим задачу сначала для случая произвольной температуры окружающей среды, а затем вычислим конечную температуру тела при температуре среды \(0^\circ.\)

Пусть начальная температура нагретого тела составляет \( = 200^\circ.\) Последующее изменение температуры описывается формулой: \[ + \left( <— > \right)> > = <+ \left( <200^\circ - > \right)>.> \] В конце первого часа тело охладилось до \(100^\circ.\) Следовательно, можно записать следующее соотношение: \[ \right) = 100^\circ = + \left( <200^\circ - > \right)>,>\;\; <\Rightarrow 100^\circ = + \left( <200^\circ - > \right)>.> \] Спустя \(2\) часа температура тела становится равной \(X\) градусов: \[X = + \left( <200^\circ - > \right)>.\] Таким образом, мы получили систему двух уравнений с тремя неизвестными: \(,\) \(k\) и \(X:\) \[\left\< \begin 100 = + \left( <200 - > \right)>\\ X = + \left( <200 - > \right)> \end \right..\] Мы не можем однозначно определить температуру тела \(X\) через \(2\) часа из данной системы. Однако можно вывести зависимость \(X\) от температуры окружающей среды \(.\) Выразим функцию \(>\) из первого уравнения: \[> = \frac<<100 - >><<200 - >>.\] Тогда \[> = <\left( <>> \right)^2> = <\left( <\frac<<100 - >><<200 - >>> \right)^2>.\] Следовательно, зависимость \(X\left( <> \right)\) имеет вид: \[ > \right) = + \left( <200 - > \right)<\left( <\frac<<100 - >><<200 - >>> \right)^2> > = <+ \frac<<<<\left( <100 - > \right)>^2>>><<200 - >>.> \] Если, например, положить температуру окружающей среды равной нулю, то температура тела через два часа будет составлять \[ = 0> \right) = 0 + \frac <<<<\left( <100 - 0>\right)>^2>>><<200 - 0>> > = <\frac<<10000>><<200>> = 50^\circ.> \] Зависимость температуры тела \(X\) от температуры окружающей среды в данной задаче показана выше на рисунке \(2.\)

Прежде всего, отметим разницу со случаем когда тело охлаждается в среде, температура которой постоянна. В этом случае температура тела формально будет бесконечно долго приближаться к температуре окружающей среды. В нашей же задаче температура среды линейно возрастает. Поэтому, рано или поздно температура тела станет равной температуре среды, то есть задача имеет решение. Будем считать также, что соблюдается квазистационарный режим, т.е. все переходные процессы в системе быстро затухают.

В таком случае процесс можно описать дифференциальным уравнением: \[\frac<

> = k\left( <— T> \right).\] По условию задачи, \( = > + \beta t.\) Следовательно, последнее уравнение можно записать в виде: \[ <\frac<

> = k\left( <> + \beta t — T> \right)>\;\; <\text<или>\;\;T’ + kT = k> + k\beta t.> \] Мы получили линейное дифференциальное уравнение, которое можно решить, например, с помощью интегрирующего множителя: \[u\left( t \right) = >> = >.\] Общее решение уравнения записывается в форме \[ >\left( > + k\beta t> \right)dt> + C>><<>>> > = <\frac<>\int <>dt> + k\beta \int <>tdt> + C>><<>>>.> \] Второй интеграл в числителе находится интегрированием по частям: \[ <\int <\underbrace <>>_\underbrace t_vdt> > = <\left[ <\begin<*<20>> >>\\ >>\\ \\ \end> \right] > = <\frac<1>>t — \int <\frac<1>>dt> > = <\frac<1>>t — \frac<1><<>>> > = <\frac<1>>\left( > \right).> \] Таким образом, закон охлаждения тела имеет следующий вид: \[ = <\frac<> \cdot \frac<1>> + k\beta \cdot \frac<1>>\left( > \right) + C>><<>>> > = <> + \beta t — \frac<\beta > + C>.> \] Постоянная \(C\) определяется из начального условия \(T\left( \right) = .\) Тогда \[C = — > + \frac<\beta >.\] Итак, процесс охлаждения тела описывается формулой \[T\left( t \right) = > + \beta t — \frac<\beta > + \left( <— > + \frac<\beta >> \right)>.\] В момент \(\tau,\) температуры тела и окружающей среды становятся равными друг другу: \[T\left( \tau \right) = > + \beta \tau .\] Время \(\tau\) определяется из уравнения: \[\require <\cancel<> + \beta \tau> = \cancel<> + \beta \tau> — \frac<\beta > + \left( <— > + \frac<\beta >> \right)>,>\;\; <\Rightarrow \left( <— > + \frac<\beta >> \right)> = \frac<\beta >,>\;\; <\Rightarrow \frac<\beta >\left( <— > + \frac<\beta >> \right) = >,>\;\; <\Rightarrow \frac<\beta >\left( <— >> \right) + 1 = >,>\;\; <\Rightarrow \tau = \frac<1>\ln \left[ <\frac<\beta >\left( <— >> \right) + 1> \right].> \] Мы можем сделать оценку времени \(\tau\) для некоторых типичных значений параметров: \[ <> = 20^<\circ>C,\;\;\;k = \frac<1><5>\,\text<мин>^<-1>,>\;\;\; <\beta = 2\,\frac<\text<град>><\text<мин>>,\;\;\; = 200^<\circ>C.> \] В результате получаем: \[ <\tau = \frac<1>\ln \left[ <\frac<\beta >\left( <— >> \right) + 1> \right] > = <\frac<1><<\frac<1><5>>>\ln \left[ <\frac<<\frac<1><5>>><2>\left( <200 - 20>\right) + 1> \right] > = <5\ln \left[ <\frac<1><<10>> \cdot 180 + 1> \right] > = <5\ln 19 >\approx <5 \cdot 2.944 >\approx <14.77\left[ <\text<мин>> \right].> \]

Источник

Расчет времени нагрева, выдержки и охлаждения при проведении термической обработки , страница 6

Примечание. Общее время нагрева штанги t_общ с учетом времени выдержки составит 36 мин + 12 мин = 48 мин, а с учетом выбранной схемы укладки (например по схеме 3 таблица 9 приложения):

t_общ = 36 × 2 + 12 = 84 мин = 1 ч 42 мин.

4 Расчет времени охлаждения

4.1 Расчет времени охлаждения в среде с постоянной температурой

Пример 4. Определить продолжительность охлаждения центра вала из стали 40Х, диаметром 600 мм, длиной 3 м с температурой 850ºС до температуры 200ºС в различных охлаждающих средах (вода, масло, воздух).

По таблице 3 приложения принимаем коэффициент теплоотдачи.

Средний коэффициент теплопроводности l_ср(от температуры нагрева до температуры охлаждения) будет равен » 37,75 Вт/м 2 °С (по таблице 5 приложения). Зная l и R находим критерий Био по формуле (13):

при охлаждении в воде:

при охлаждении в масле:

при охлаждении на воздухе:

Определяем температурный критерий q(для случая охлаждения):

Для случая охлаждения в воде или на воздухе:

Для случая охлаждения в масле:

Тогда критерий Фурье, определенный по рисунку А.1, б (приложение):

при охлаждении в воде Fo= 0,4 (Bi = 9,03; θ = 0,21);

при охлаждении в масле Fo = 0,68 (Bi = 2,77; θ = 0,19); при охлаждении на воздухе Fo = 1,4 (Bi = 0,79; θ = 0,21).

Коэффициент теплопроводности взят для аустенитного состояния при 800ºС, λ = 26,7 Вт/мºС (таблица 5, приложение), теплоемкость С = 687 Дж/кгºС (таблица 6, приложение) и γ = 7830 кг/м 3 .

Определим коэффициент температуропроводности по формуле (21):

Критерий Фурье по формуле (20):

Подставляя значения Foдля различных сред охлаждения, находим: при охлаждении в воде:

при охлаждении в масле:

при охлаждения на воздухе:

4.2 Расчет времени охлаждения в среде о переменной

4.2.1 Расчет времени охлаждения в масле

Пример 5. Определить время охлаждения центра вала диаметром 200 мм, длиной 3 м, весом 700 кг с температурой 800ºС до 200ºС в баке о маслом объемом 4 м 3 при начальной температуре масла 30ºС.

«Водяное число» масла при удельном весе γ_ж = 0,9 кг/л с теплоемкостью С_ж = 2,06 кДж/кгºС определим по формуле:

где V_ж – объем жидкости (масла);

γ_ж – удельный вес жидкости (масла);

С_ж – теплоемкость жидкости (масла).

«Водяное число» вала весом G_м = 700 кг и с теплоемкостью С_м = 0,687 кДж/кгºС (таблица 6, приложение) определим по формуле:

Отношение «водяных чисел»:

Подставляя значения, «водяных чисел» в уравнение (23) получим:

Следовательно, температура масла повысится с 30º до 78ºС, т.е. на 48ºС, а температура охлаждаемого металла снизится с 800º до 800 – 78 = 722ºС.

Принимая a =581,5 Вт/м 2 ºС (см. пункт 1.4), l =34,9 Вт/м 2 ºС (таблица 5, приложение).

Подставляя наеденные значения (для встречного потока) в уравнение (26) получим:

Значение температурного коэффициента θ находим по формуле (19):

По значениям Bi_усл=1,61 и θ=0,17 по рисунку А.1, б (приложение) находим Fo=0,8, что соответствует расчетным данным по формуле (20), которая была преобразована в формулу (22), определяем время охлаждения:

Поскольку охлаждение ведется в баке с маслом, без принудительного охлаждения его происходит постепенное повышение его температуры за счет вносимого металлом тепла. Для того, чтобы при закалке не происходило резкого повышения температуры масла, рекомендуется принимать отношение веса жидкости к весу закаливаемого металла равным:

В нашем примере

4.2.2 Расчет времени охлаждения изделий при душевой закалке

Пример 6: Определить время охлаждения сложных профилей при душевой закалке: швеллера №20 (200×55×3,2 мм), уголка №9 (90×90×6 мм), балки №20 (200×65×3,2 мм) с температуры конца прокатки (1000ºС) до температуры начала самоотпуска 450ºС при закалке изделий обрызгиванием (душевая закалка) для малоуглеродистой и низколегированной сталей.

Определим вес изделий: