Гидростатическое давление
Калькулятор находит неизвестные величины по заданным, используя формулу давления столба жидкости.
Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:
Калькулятор позволяет найти
- давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
- высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
- плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
- ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости
Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения — земное ускорение, и для давления — величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.
Гидростатическое давление
Гидростатическое давление — давление столба воды над условным уровнем.
Формула гидростатического давления выводится достаточно просто
Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
В 1648 г. это продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Также это приводит к такому явлению как гидростатический парадокс.
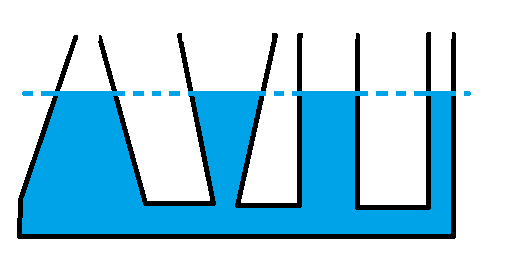
Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.
На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда
Источник
Как рассчитать высоту на которую нужно поднять емкость для капельного полива в 250 литров?
Есть емкость в 250 литров и хочу поставить на подставку, на какую высоту её поднимать, чтоб вода без проблем проходили по капельной ленте и выбегала полностью! Говорят, что фактически и пол метра хватит, лишь бы чуть подъём был и кран с фильтром под бочкой вмещались!
Если прочитать описание на упаковке капельной ленты или просто порыться в интернете, то выяснится, что капельной ленте необходимо давление для нормальной работы в пределах от 0.5 до 1 атмосфер.
Всего ничего!
Больше одной атмосферы даже не рекомендуется, теперь возьмём минимум 0.5 бар (атмосферы) — как его создать, куда поднять и как подключить?!
Разберёмся с бочкой, 250-вая бочка имеет высоту примерно 1.2 метра — то есть на каждый квадратный сантиметр на дне бочки давит 120 кубиков, а это уже больше килограмма, а соответственно больше 1 атмосферы, получается будет работать даже без подъёма, но вода сойдёт только до уровня примерно 50-60 см от дна, так как давление упадёт ниже 0.5 бар и капля просто стане, (она конечно вытечет, но неравномерно польёт участок) и конечно ещё нужно прибавить потери давления на штуцер (врезку, слив и кран).
Отсюда уже делаем логический вывод, чтоб капельный полив работал, от 250 — вой бочки её достаточно поднять, немного выше уровня мёртвой линии — то есть примерно на 70-80 см от поверхности поливаемого участка!, но добавим на потери патрубка и соединяющего водопровода и получим максимум 1 метр поднятой бочки, при желаемом минимуме в 0.5 атмосфере на уровне земли в шланге.
А что если я подниму бочку на 3 или 4 метра, что будет. да ни чего не будет, капля будет через силу неравномерно поливать огурцы и помидоры, на всех стыках будет сочится вода, плюс к этому вы создадите дополнительные трудности с обслуживанием, да и соседи не поймут (те кто понимают конечно).
Ну, бред же! Инженеры, блин! 120 см водяного столба у него — больше атмосферы! Ха три раза! Если грубо, одна атмосфера — 10 метров воды! В школу, срочно на второй год!
Андрей Питерский уже высказался. Но «истина не тускнеет от повторения!»
О,еще один просветленный, Стэлс. К сожалению, видимый.))) У него тоже 1 метр воды — 1 атмосфера. Да вы, ребята, воду со ртутью перепутали! — 6 месяцев назад
Для расчета высоты установки емкости для капельного полива, можно взять за отсчет давление столба воды, которая как известно имеет постоянный вес, и гравитация также имеет постоянную силу. Можно говорить что давление воды увеличивается пропорционально увеличению высоты емкости над уровнем излива (расположения форсунки, капельницы) Так на высоте 50 сантиметров, давление будет 0,5 атмосферы. Это значит что дно бочки должно находится как минимум не ниже полуметра над землей (а точнее над уровнем капельной ленты) Отсюда можно и считать необходимую высоту. При поднятии емкости на высоту один метр, мы получим давление 1 Атмосферу, на высоту двух метров — 2 Атмосферы. Необходимо ли поднимать нашу емкость выше, зависит от общей протяженности капельных лент, и количества форсунок. Давление в системе будет меняться обратно пропорционально удаленности форсунок от емкости. Чем дальше расположена форсунка, тем реже будет каплеобразование, нежели у форсунок расположенных ближе к емкости, поэтому самым оптимальным вариантом, влияющим на качество полива, является не только высота поднятия емкости, но и регулируемые капельницы, проходной объем воды которых можно настроить — ближе к емкости немного ограничить, а дальше от емкости приоткрыть несколько больше. При одинаковых проходных отверстиях, почва ближе к емкости орошается сильнее, происходит залив, а в удалении от нее, наоборот — растениям не хватает влаги.
При устройстве поливочного коллектора из труб, питающегося из одной емкости и питающего несколько магистралей, принимайте во внимание (при выборе высоты установки емкости) и то что давление будет делиться между несколькими поливными лентами.
То что вам говорят что хватит и 0,5 метра, это не совсем правильно. После того как бочка вытечет полностью, давление упадет ниже 0,5 атмосфер, и далее будет сильно падать. Вытечет бочка возможно и полностью, однако полив будет происходить очень долго, может длится до суток. А поливать лучше в течении ночных часов, так как вода меньше испаряется и её больше достается растениям. Поднимите хотя бы на метр, тогда вы получите до самого опорожнения бочки почти 1 атмосферу давления столба воды. Оптимальной высотой для бочки ваших объемов (250 литров) будет 1-1,5 метра.
Более высокое расположение емкости, считаю не рациональным, поскольку не столько положительно скажется на давлении, сколько осложнит монтаж емкости.
Источник
Конвертер величин
Калькулятор гидростатического давления
Этот калькулятор гидростатического давления определяет гидростатическое давление, действующее на тело, находящееся в жидкости на определенной глубине.
Пример: Рассчитать давление, действующее на аквалангиста на глубине 15 м. Плотность морской воды 1022 кг/м³ и атмосферное давление 101325 Па.
Для расчета введите единицы и нажмите кнопку Рассчитать.
Определения и формулы
Гидростатика — раздел физики, изучающий жидкости в состоянии равновесия, в частности, при воздействии на них гравитационного поля. В отличие от гидродинамики, изучающей движение жидкостей и силы, действующие на твердые тела, погруженные в движущиеся жидкости, гидростатика изучает механические свойства и поведение жидкостей в покое, в устойчивом равновесии. Гидростатика, в частности, изучает давление, оказываемое несжимаемыми жидкостями на погруженные в них тела.
Гидростатика широко применяется в метеорологии, медицине (изучение давления в кровеносных сосудах), биологии, инженерном деле, например, при разработке оборудования для использования и транспортировки жидкостей или при проектировании плотин. Гидростатика объясняет многие явления, встречающиеся в повседневной жизни, например, почему предметы могут плавать или тонуть в воде или почему поверхность спокойной воды горизонтальна и перпендикулярна направлению силы тяжести.
Гидростатическое давление — давление вследствие силы тяжести находящейся в равновесии жидкости в любой точке внутри этой жидкости. Оно увеличивается пропорционально глубине жидкости, так как чем глубже погружено тело в воде, тем больше жидкости вес жидкости, который действует на ту же поверхность (подробнее о давлении — в наших калькуляторе давления and конвертере давления). Гидростатическое давление определяется приведенной ниже формулой, называемым основным уравнением гидростатики, которая и используется в нашем калькуляторе:
где P — гидростатическое давление, измеряемое в системе СИ в паскалях (Па), ρ — плотности жидкости, измеряемая в килограммах на кубический метр (кг/м³), P0 — внешнее давление, измеряемое в паскалях, которое обычно является атмосферным давлением (P0 = 101325 Па), g ускорение свободного падения, измеряемое в метрах в секунду за секунду (м/с²), и h — глубина жидкости, измеряемая в метрах (м).
Значение h может также относиться к высоте и это уравнение можно использовать для определения давления столба жидкости указанной высоты.
Отметим, что это уравнение не содержит общей массы или объема жидкости, так как давление не зависит от формы сосуда, массы жидкости или ее полного объема — давление на любой глубине остается одинаковым при любой форме сосуда, в который налита жидкость.
Основные свойства жидкостей были независимо открыты французским математиком, физиком и изобретателем Блезом Паскалем (1623–1662) и голландским математиком Симоном Стевином (1584-1620) и основное уравнение гидростатики в англоязычной литературе иногда называют законом Стевина. Следует отметить, что Стевин определил величину гидростатического давления до Паскаля, однако Паскаль не знал голландского и работ Стевина не читал.
Поскольку в результате наличия гравитационного поля на погруженные в жидкость тела действует гидростатическое давление, на все погруженные в жидкость тела действует также выталкивающая сила. Закон, определяющий выталкивающую силу, действующую на полностью или частично погруженные в жидкость плавающие предметы, был открыт Архимедом, который большую часть жизни прожил в Сиракузах на Сицилии. Он предположил, что эта сила равна весу жидкости, вытесненной телом.
В связи с высоким давлением под водой и необходимостью медленного всплытия, водолазы могут работать, например, на глубине 35 м всего 30 минут. Для увеличения рабочего времени используется метод длительного пребывания под давлением в режиме насыщения. Он позволяет водолазам дольше работать на больших глубинах без риска возникновения декомпрессионной (кессонной) болезни. При использовании этого метода водолазы живут в жилых барокамерах на поверхности или под водой. Из жилой барокамеры водолазов перемещают под воду в место выполнения работ и обратно в закрытом водолазном колоколе, называемом также капсулой для транспортировки персонала (англ. personnel transfer capsule). Капсула представляет собой усовершенствованный водолазных колокол в форме цилиндра (показанного на фотографии) или сферы, который вмещает двух или трех человек. На наружной стороне капсулы установлены баллоны для хранения дыхательной смеси.
Источник
как расчитать напор воды
Если кто помнит физику 7-8 класса подскажите формулу, чтобы просчитать с какой силой будет течь вода из бака объёмом А, поднятого на высоту В?
Объем вообще здесь ни при чем. Давление на глубине h до поверхности воды в баке, в точности равно высоте водяного столба h. 
То есть: если глубина 1м, то давление равно 1метр водяного столба или в привычных единицах- 0,1кг/кв.см. Если 10м = 1кг/кв.см
Понять это очень просто: представляете квадратный столбик воды с основанием площадью один кв.см. и высотой 1 метр(или 10метров). Каков объем воды?
-в первом случае (если 1 метр)- 100 куб.см. такой объем воды весит 100граммов, или 0,1 кг.
-во втором случае (10 метров) — 1000 куб.см. Такой объем воды весит ровно 1кг. Вот этими килограммами и давит = развивает давление.
Геометрические размеры, форма бака, длина трубы/шланга никакого значения для формирования давления не имеют. Только перепад высоты от поверхности воды в баке до места измерения давления.
Другое дело, как Вы пишете, «с какой силой будет течь». Это зависит и от гидравлического сопротивления трубы/шланга (в том числе и от диаметра), наличия вентилей, кранов и т.п.
Принято считать, что на 100 метрах горизонтальной трубы падает давление 1 кг/кв.см. («пионерский» расчет)
Итак: имея бак с уровнем воды 5 метров от поверхности земли и трубу с краном с присоединенным шлангом длиной 50 метров, лежащим на земле, можем утверждать, что статическое давление воды в шланге в некоторой близости от обреза шланга равно 0,5 кг/кв.см (если шланг заткнуть, то и манометр на конце шланга так покажет). Но если шланг открыть, то при движении воды гидравлическое сопротивление потоку будет также около 0,5 кг/кв.см. Конечно, вода не встанет, но будет течь вялой струёй. Практически без давления.
Источник