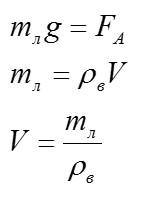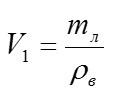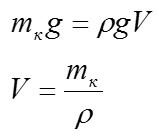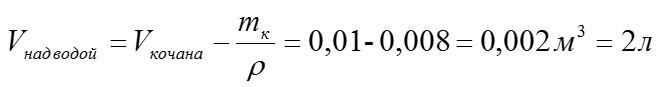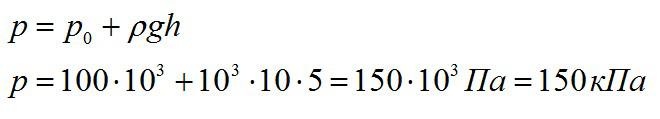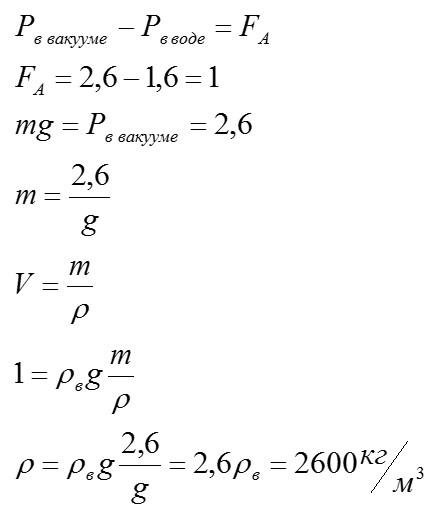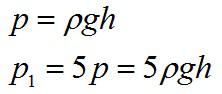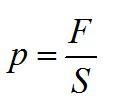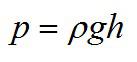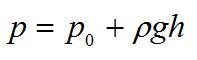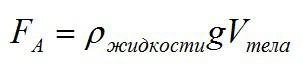Решение задач с кувшинами с водой

Задачи на переливания

Это учебная статья по математике, перед началом занятий мы рекомендуем ознакомиться с вводной частью

Все задачи на переливания принципиально делятся на 2 типа.

Первый – когда у нас есть много жидкости (озеро, бесконечно большая бочка, водопровод), и мы можем наполнять доверху сосуды сколь угодно большое количество раз, то есть количество жидкости не ограничено. При этом мы можем безбоязненно выливать воду из сосудов.

Второй – это когда жидкости у нас ровно столько, сколько изначально налито в сосудах (в этом случае у нас обычно не простая жидкость, а какая-либо особенная: молоко, сок и т. д.). Чаще всего эту жидкость ещё и нельзя проливать – авторы стараются это отдельно оговаривать. Если же мы можем выливать жидкость, то в условиях задачи обычно присутствует какой-либо персонаж, который может пить данный тип жидкости: Кот Баюн, сосед Гриша и т. п.

Также стоит понять принцип задач на переливания: например, если у нас есть сосуд объемом 8 литров и 5 литров, и нам надо отмерить 2 литра воды, мы не имеем права на следующее решение: «Наполним восьмилитровый сосуд на четверть – таким образом, мы и получим 2 литра воды». Или: «Давайте опустошим наш 5 литровый сосуд на 60%, тогда в нем останется ровно 2 литра воды». Нет, так делать нельзя. (Если у ребёнка в этом месте возникают вопросы, то вы можете придумать, например, такое оригинальное объяснение: «А вдруг наш сосуд – это какая-нибудь замысловатая ваза (или древняя амфора), конечно, без шкалы делений!» Или даже просто банка не вполне симметрична, а на глаз определить середину – проблематично…) Мы можем либо полностью наполнять сосуды, либо полностью опустошать их, либо переливать из одного сосуда в другой. При этом мы можем пользоваться тем, что при этих операциях часть воды может оставаться в сосуде, из которого дополняется другой сосуд.

Для примера решим три задачи.

Задача 1-го типа

Для приготовления компота маме нужно налить в 5-литровую кастрюли 4 литра воды. Как маме справиться с этой задачей, если у мамы есть кроме этой кастрюли ещё 3-литровая банка, водопроводный кран и раковина, куда можно выливать воду?

Решение.

Нальём в 3-литровую банку воду и перельём её в кастрюлю. Затем еще раз наполним банку и выльём в кастрюлю, сколько поместится. Тогда в кастрюле будет 5 литров и 1 литр в 3-литровой банке. Теперь выльем всю воду из кастрюли в раковину. Затем перельем литр из банки в кастрюлю и добавим ещё три литра, наполнив банку ещё раз. Теперь в кастрюле 1 + 3 = 4 литра, что и требовалось. Задача решена.

Наше решение можно проиллюстрировать таблицей:

Итак, мы получили желанные 4 литра. Задача решена! Мы считаем, что такой способ решения с помощью таблицы является достаточно наглядным, и рекомендуем для вашего совместного с ребёнком решения.

Задача 2-го типа

У Марьи есть 2 кувшина объёмом 8 и 3 литра. В восьмилитровом кувшине налит весь имеющийся у Марьи кисель. Как отмерить 2 литра киселя? Все излишки киселя можно отдать Коту Баюну, который просто обожает это лакомство.

Решение.

Наполним трехлитровый кувшин доверху из восьмилитрового, после этого у нас будет 5 литров в 8-литровом и 3 литра в 3-литровом. Отдадим весь кисель из 3-литрового кувшина Коту Баюну. После этого у нас осталось 5 литров в 8-литровом и 3-литровый кувшин пуст. Снова наполним 3-литровый кувшин из 8-литрового. После этой операции в 8-литровом кувшине у нас останется ровно 2 литра (5 – 3 = 2). Мы отмерили 2 литра. Задача решена!

Решение также можно проиллюстрировать таблицей:

Ещё одна задача 2-го типа

Задача 3.

В кастрюле налито 8 литров супа. Есть также пустые 3-х и 5-тилитровая банки. Требуется отмерить 4 литра супа. Как это сделать, если суп нельзя проливать?

Решение.

1 способ. Нальём суп доверху в меньшую банку, затем перельём полученные три литра в 5-литровую банку, а 3-литровую наполним снова. Теперь будем лить суп из 3-литровой банки в 5-литровую, пока она не наполнится доверху. Тогда в меньшей банке останется 1 литр (5 – 3 = 2 и 3 – 2 = 1). Перельём 5 литров в кастрюлю, а 1 литр – в большую банку. Затем перельём 3 литра из кастрюли в меньшую банку. После этого в кастрюле останется ровно 4 литра. Задача решена.

2 способ. Нальём суп доверху в большую банку, тогда в кастрюле останется ровно 3 литр. Перельём из большой банки в меньшую 3 литра, после чего перельём их в кастрюлю. Перельём 2 литра из большой банки в меньшую, и наполним большую банку доверху супом из кастрюли. После чего дольём меньшую банку (там было 2 литра, а помещается 3) из большей банки. Получим 4 литра в большой банке. Задача решена.

Проиллюстрируем оба способа таблицам:

Советуем использовать таблицу при решении подобных задач.

Также ребёнку можно дать следующую подсказку. Речь пойдет о задачах, где разрешается выливать жидкости. Пусть в какой-то момент наполнены все сосуды, может быть, частично. Тогда перед ребенком стоит вопрос о том, откуда вылить жидкость. Выливать стоит из полного сосуда, а не из полупустого, так как количество литров в полном сосуде мы всегда с лёгкостью снова получим, тогда как получить полупустой сосуд − дело затруднительное. Надеемся, что в процессе работы вы сами сможете придумать множество оригинальных приемов и способов!

Обратите внимание, что приведённые решения могут не являться единственными. Ни в коем случае не говорите ребёнку, что он как-то не так стал решать задачу, если первым ходом он, допустим, налил воду из крана не в больший, а в меньший сосуд! Просто тщательно следите за его действиями. В большинстве задач есть как минимум 2 способа решения, и, скорее всего, при правильном выполнении переливаний ваш ребёнок в конечном итоге получит результат. Правда, возможно, за большее число ходов, зато – сколько удовольствия от самостоятельного решения без подсказок он получит!

Испытайте свои знания!

Для самых умных и талантливых учеников мы проводим на сайте дистанционную интернет-олимпиаду. Сразу же после прохождения олимпиады показываются результаты и полный разбор задач для работы над ошибками. В зависимости от успехов олимпиадника выдаются электронные дипломы и похвальные грамоты.

Каждый участник получает электронный сертификат участника.

Источник

Как отмерить 4 литра воды с помощью двух вёдер по 5 и 3 литр? Задача для собеседования.

Эту задачу я узнал от одного коллеги, который пробовался на работу в Google. Он работал у нас Айтишником.

Однажды мы разговорились на тему собеседования, и наш диалог зашел про вопросы на тестировании для кандидатов.

Я считаю, что на собесе очень нервная остановка и на тестах кандидат не может себя проявить в полную меру.

На что мне мой коллега ответил, что это наоборот показывает стрессоустойчивость и способность сконцентрировать внимание на одной задачи, а если еще и оценить время, на которое он потратит на решение, то можно сделать много выводов.

Ну, не знаю он айтишник, может ему виднее.

Для примера он мне дал одну задачу, которую ему задавали при наборе в Google.

Эта задача начального уровня и кандидат на должность программиста должен с ней легко справляться за минуту.

После того, как он мне её показал, я тоже решил использовать у себя на собеседованиях, и оценивать за какое время её осилит мой будущий работник.

Задача очень легкая, и если он её не решает, дальше речи о трудоустройстве быть не может.

Условия задачи простые.

У вас есть два ведра по 5 и 3 литра, как с помощью этих этих емкостей можно отмерить ровно 4 литра воды? При этом количества воды и попыток не ограниченно.

Сейчас уже у моей команды есть много разных способов решения этой задачи, и они постоянно делятся ими со мной, вспоминая, как я их тестировал при приеме на работу.

Но больше всего их удивляло, что они шли на должность менеджеров по продажу, а их просили переливать воду. :))).

Используйте эту задачу при тестировании своих кандидатов, очень здорово помогает набирать правильных людей.

Ах, да, чуть не забыл сказать ответ на эту задачу.

Значит, что делаем, для того, чтобы у нас получилось 4 литра вода.

а) Наливаем в трехлитровое ведро до краев воды и переливаем в ведро 5 литров.

б) Далее еще раз набираем трехлитровое до края и дозаполняем два литра в пятилитровое до краев. Итого у нас в трехлитровом остается 1 литр воды.

в) Далее выливаем всю воду из пятилитрового ведра

г) Заливаем 1 литр из ведра в 3 литра в 5 литров, и теперь в 5 литровки у нас ровно 1 литр

д) Наливаем полное трехлитровое ведро и переливаем в 5-литровое.

Итого у на ровно 4 литра в 5- литровом ведре.

5 литровое ведро выливаем в трех литровое.

Итого остается 2 литра в пятилитровом.

Далее опустошаем трехлитровое и наливаем туда два литра из пятилитрового.

Наполняем до краев пятилитровое и переливаем недостающий литр в трехлитровое. Итого в пятилитровом ведре ровно 4 литра воды.

Источник

Задачи по гидростатике с решениями

• 12 Январь 2021
• 10 минут
• 25 773

В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».

За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.

Задачи по гидростатике с решениями

Задача №1 на гидростатику

Условие

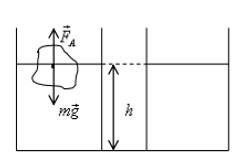
B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?

Решение

По условию плавания тел:

V – объем погруженной в воду части льда. После таяния льда образуется объем воды:

Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.

Ответ: уровень не изменится.

Задача №2 на гидростатику

Условие

Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?

Решение

Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:

Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:

В одном кубическом метре – тысяча литров.

Ответ: 2 литра.

Задача №3 на гидростатику

Условие

Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.

Решение

Вспоминаем основное уравнение гидростатики и записываем:

Ответ: 150 кПа.

Задача №4 на гидростатику

Условие

Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.

Решение

Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.

Ответ: 2600 кг/м3.

Задача №5 на гидростатику

Условие

Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?

Решение

Формула для гидростатического давления:

Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.

Ответ: высота увеличилась в 5 раз.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Вопросы по гидростатике

Вопрос 1. Что такое гидростатический парадокс?

Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.

Вопрос 2. Какие есть внесистемные единицы изменения давления:

Ответ. Внесистемные единицы давления:

• миллиметр ртутного столба;
• бар;
• атмосфера.

Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?

Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).

Вопрос 4. Что такое сообщающиеся сосуды?

Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.

Вопрос 5. Что такое гидравлический пресс?

Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.

Гидростатика: немного теории

Гидростатика – раздел физики, изучающий равновесие жидкостей.

Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?

Давление и плотность

Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.

Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:

Греческое «ро» — плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.

Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.

Закон Паскаля и основное уравнение гидростатики

Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.

Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.

В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.

В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.

Закон Архимеда и условия плавания тел

Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:

На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.

Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.

Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.

Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.

Источник