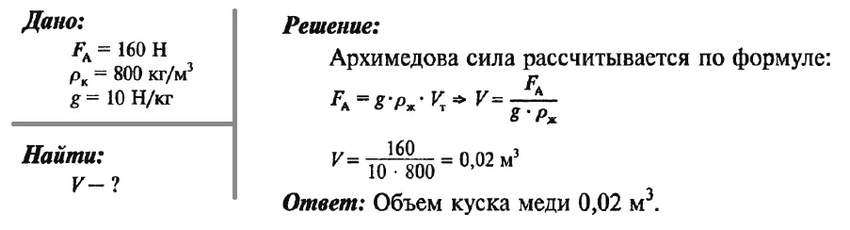Решение задачи сосуд с водой

Логические задачи на переливания

Логические задачи на переливания с решением

Задача 1.

Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?

Задача 2.

Деление 10 л поровну, имея сосуды 3, 6 и 7 л.
Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 3.

Деление 8 л поровну, имея сосуды 8, 5 и 3 л.
Разделить на две равные части воду, находящуюся в полном 8 литровом сосуде, пользуясь этим и пустыми 5- и 3-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 4.

Деление 16 л поровну, имея сосуды 6, 11 и 16 л.
Разделить на две равные части воду, находящуюся в полном 16 литровом сосуде, пользуясь этим и пустыми 11- и 6-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 5.

Два сосуда и кран с водой.
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л?

Решения задач.

Решение задачи 1.

Наливаем кастрюлю.
Переливаем воду из кастрюли в банку.
Наливаем кастрюлю.
Доливаем полную банку, и в кастрюле остается 3 литра.

Решение задачи 2.

В скобках – второй вариант решения.

Сосуд 6 л	Сосуд 3 л	Сосуд 7 л
До переливания	4	0	6
Первое переливание	1 (4)	3 (3)	6 (3)
Второе переливание	1 (6)	2 (1)	7 (3)
Третье переливание	6 (2)	2 (1)	2 (7)
Четвертое переливание	5 (2)	3 (3)	2 (5)
Пятое переливание	5 (5)	0 (0)	5 (5)

Решение задачи 3.

Сосуд 8 л	Сосуд 5 л	Сосуд 3 л
До переливания	8	0	0
Первое переливание	3	5	0
Второе переливание	3	2	3
Третье переливание	6	2	0
Четвертое переливание	6	0	2
Пятое переливание	1	5	2
Шестое переливание	1	4	3
Седьмое переливание	4	4	0

Решение задачи 4.

Сосуд 16 л	Сосуд 11 л	Сосуд 6 л
До переливания	16	0	0
Первое переливание	10	0	6
Второе переливание	10	6	0
Третье переливание	4	6	6
Четвертое переливание	4	11	1
Пятое переливание	15	0	1
Шестое переливание	15	1	0
Седьмое переливание	9	1	6
Восьмое переливание	9	7	0
Девятое переливание	3	7	6
Десятое переливание	3	11	2
Одиннадцатое переливание	14	0	2
Двенадцатое переливание	14	2	0
Тринадцатое переливание	8	2	6
Четырнадцатое переливание	8	8	0

Решение задачи 5.

Если сначала наполнить 11-литровый сосуд, то потребуется 18 переливаний, а если 7-литровый, то, как следует из рисунка, – всего 14.

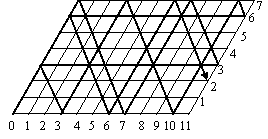
Логические задачи на переливания с решением

Источник

Решение задачи сосуд с водой

Краткая теория, используемая для решения задачи на сообщающиеся сосуды. Подробнее смотрите в конспекте «Сообщающиеся сосуды. Гидравлический пресс. Шлюзы».

Сообщающиеся сосуды — два или более соединённых между собой сосудов (ниже уровни жидкости), в которых жидкость может свободно перетекать из одного сосуда в другой.

Закон сообщающихся сосудов : в открытых сообщающихся сосудах любой формы при равновесии давление жидкости на любом горизонтальном уровне одинаково.

Схематически это выглядит таким образом, что в точках А и В ⇒ р _A = р _B .

ρ₁gh₁ + ρ₂gh₂ = ρ₃gh₃ + ρ₄gh₄

Обратите внимание! Ниже уровня, на котором находятся точки А и В, жидкость однородна. Обозначения : р — давление, ρ — плотность, h — высота, g — ускорение свободного падения (9,8 м/с^2).

Следствие 1 : в открытых сообщающихся сосудах при равновесии высоты столбов жидкостей, отсчитываемые от уровня, ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей.
Следствие 2 : в открытых сообщающихся сосудах при равновесии однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. В левом колене сообщающихся сосудов налита вода, в правом — керосин. Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.

Ответ: 0,04 м (или 4 см). Чтобы увидеть решение задачи, нажмите на спойлер ниже.

Задача № 2. В сообщающихся сосудах находятся ртуть и вода. Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?

Ответ: 0,85 м (или 85 см).

Задача № 3. В сообщающихся сосудах находятся ртуть, вода и керосин. Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?

Ответ: 0,335 м (или 33,5 см).

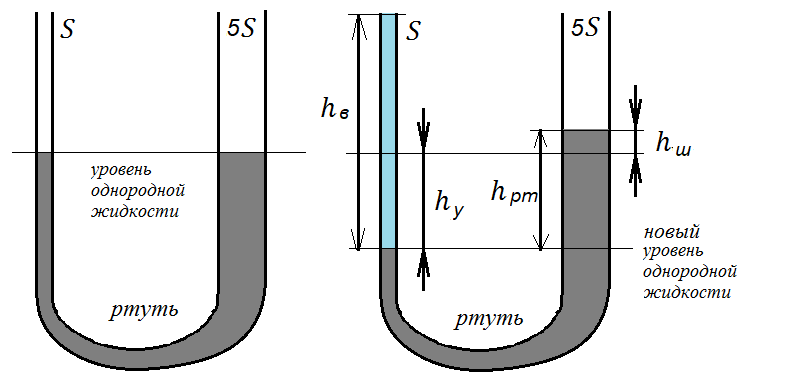
Задача № 4. В цилиндрических сообщающихся сосудах находится ртуть. Площадь поперечного сечения широкого сосуда в пять раз больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают воду, которая образует столб высотой 34 см. На сколько поднимется уровень ртути в широком сосуде и на сколько опустится в узком?

Ответ: в широком сосуде на 0,42 см, в узком — на 2,1 см.

Исходное положение уровня ртути показано на левом рисунке. Обозначим высоту, на которую поднялся уровень ртути в широком колене h_ш. Тогда объем этого столбика равен V = h_ш • 5S – так как площадь сечения широкого сосуда в пять раз больше, чем узкого.
Раз объем ртути в широком колене увеличился, то очевидно, что увеличился он за счет уменьшения объема в узком. Там высота столба ртути уменьшилась на высоту, точно соответствующую найденному объему. Раз сечение узкого колена меньше, чем широкого, то высота, на которую опустилась ртуть в узком сосуде, равна h_y = V/S = (h_ш • 5S)/S = 5h_ш.
Давление столба воды в левом колене равно давлению столба ртути над уровнем однородной жидкости в правом:
ρ_вgh_в = ρ_ртgh_рт. По рисунку мы можем выразить h_рт = h_ш + h_у и сократить уравнение на g:
ρ_вh_в = ρ_рт(h_ш + h_у). Ранее мы определили h_у, следовательно:
ρ_вh_в = ρ_рт(h_ш + 5h_ш) или ρ_вh_в = 6ρ_ртh_ш. Найдем h_ш:
h_ш = ρ_вh_в : 6ρ_рт = 1000 • 0,34 : (6 • 13600) = 340 : 81600 = 0,0042 (м) или 0,42 (см).
h_y = 5h_ш = 5 • 0,0042 = 0,021 (м) или 2,1 (см).

Задача № 5. Высота воды в левом колене сообщающихся сосудов h₁ = 40 см, в правом h₂ = 10 см. В каком направлении будет переливаться вода, если открыть кран? На сколько изменится уровень воды в левом сосуде? Найти объем воды, который перелился из одного сосуда в другой. Левое колено сосуда имеет площадь поперечного сечения S₁ = 10 см 2 , правое S = 20 см 2 .

Ответ: в правый; 0,2 м; 0,2 л.

Источник

Решение задачи сосуд с водой

Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».

Название величины

Обозначение

Единица измерения

Формула

Объем тела

V_т = F_A / pg

Плотность жидкости

кг/м 3

p_ж = F_A / (Vg)

Сила Архимеда

F_A = p_ж V_т g

Постоянная

g ≈ 10 Н/кг

Физика 7 класс: все формулы и определения МЕЛКО на одной странице

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Тело объемом 2 м 3 погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2. Определить выталкивающую силу, действующую на деревянный плот объемом 12 м 3 , погруженный в воду на половину своего объема.

Задача № 3. Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4. Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5. Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6. Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

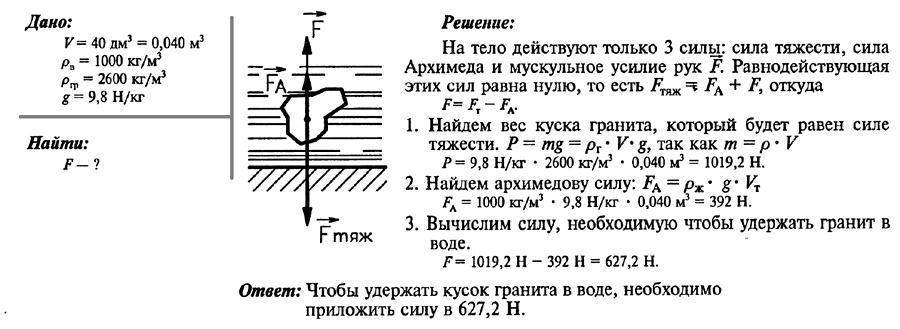
Задача № 7. Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм 3 ?

Задача № 8. Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.

Задача № 9 (повышенной сложности). Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности). Рассчитайте, какой груз сможет поднять шар объемом 1 м 3 , наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11. Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м 3 .

Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V₁ – объем цилиндра, погруженного в масло (V₁ = V – V₂ = Sh₁); h₁ – высота части цилиндра, погруженной в масло; V₂ – объем цилиндра, погруженного в воду после добавления масла; р_в – плотность воды (1000 кг/м 3 ); р_м – плотность масла (800 кг/м 3 )

Найти : (h – h₁) / h — ?

Решение . F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9p_вgV
F₁ – сила, выталкивающая цилиндр из масла F₁ = p_мgV₁
F₂ – сила, выталкивающая цилиндр из воды после добавления масла F₂ = p_вgV₂
Баланс сил: F – F₁ = F₂
0,9p_вgV – p_мgV₁ = p_вgV₂ V₁ = V – V₂ ⇒ 0,9p_вV – p_м(V – V₂) = p_вV₂

V(0,9p_в – p_м) = V₂(p_в – p_м) V = Sh; V₁ = Sh₁ ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).

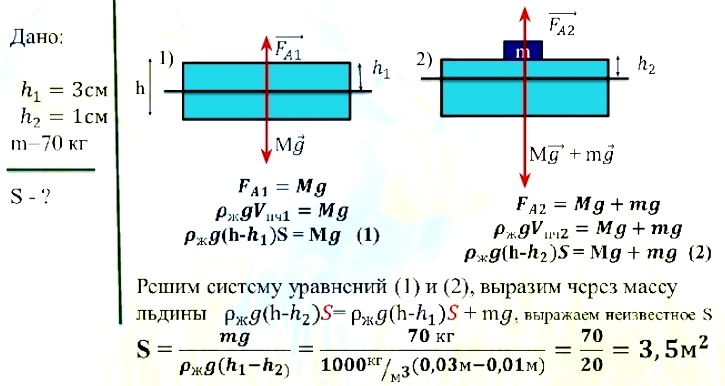
Задача № 12. Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.

Ответ: 3,5 м 3 .

Теория для решения задач.

Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = р_атм + p*g*h

Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».

Источник