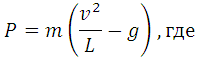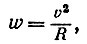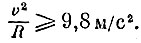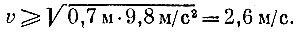Если достаточно быстро вращать
27958. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю.
В верхней точке сила давления, выраженная в ньютонах, равна
m — масса воды в килограммах,
v — скорость движения ведeрка в м/с,
L — длина верeвки в метрах,
g — ускорение свободного падения (считайте g = 10 м/с 2 ).
С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верёвки равна 40 см? Ответ выразите в м/с.
Понятно, что чем выше скорость вращения, тем больше давление воды (в том числе и в верхней точке). Нам необходимо найти минимальную скорость, при которой вода не будет выливаться, то есть скорость, при которой давление в верхней точке будет равным нулю (вода как бы зависнет) Р = 0. Решаем уравнение, сантиметры переводим в метры (40см = 0,4м):
Произведение равно нулю, когда один из множителей равен нулю, m≠ 0 (это масса воды), значит
При скорости вращения 2 м/с вода выливаться не будет. Если же скорость будет от 0 до 2 м/с давление в верхней точке будет отрицательным и вода выльется.
Источник
Сила давления вращения ведерка с водой
Ведерко с водой, привязанное к веревке длиной l = 60 см, равномерно вращается в вертикальной плоскости. Найти наименьшую скорость v вращения ведерка, при которой в высшей точке вода из него не выливается. Какова сила натяжения веревки T при этой скорости в высшей и низшей точках окружности? Масса ведерка с водой m = 2 кг.
l = 60 см = 60·10 -2 м

Решение:
На тело действуют три силы: сила тяжести, центростремительная сила, возникающая из-за вращения ведерка и сила натяжения нити. 2- й закон Ньютона запишется в виде:
где равнодействующая сила :
В верхней точке:
Проеция на ось Y :
В верхней точке, если давление на стенки ведра отсутствует и вода при этом не вылевается из ведра, то

Минимальная скорость, при которой это возможно. С учётом того, что
2- й закон Ньютона запишется в виде:
где равнодействующая сила:
Проеция на ось Y :
Ответ:
Источник
Сила давления вращения ведерка с водой
«Уничтоженная» тяжесть
«Вода не выливается из сосуда, который вращается,- не выливается даже тогда, когда сосуд перевернут дном вверх, ибо этому мешает вращение»,- писал две тысячи лет назад Аристотель. На рис. 31 изображен этот эффектный опыт, который, без сомнения, многим знаком: вращая достаточно быстро ведерко с водой, вы достигаете того, что вода не выливается даже в той части пути, где ведерко опрокинуто вверх дном.
Обычно объясняют это явление «центробежной силой», понимая под ней ту воображаемую силу, которая будто бы приложена к телу и обусловливает стремление его удалиться от центра вращения. Этой силы не существует: указанное стремление есть не что иное, как проявление инерции, а всякое движение по инерции осуществляется без участия силы. В физике под центробежной силой разумеют нечто иное, а именно — ту реальную силу, с какой вращающееся тело натягивает удерживающую его нить или давит на свой криволинейный путь. Сила эта приложена не к движущемуся телу, а к препятствию, мешающему ему двигаться прямолинейно: к нити, к рельсам на криволинейном участке пути и т. п.
Обращаясь к вращению ведерка, попытаемся разобраться в причине этого явления, не прибегая к двусмысленному понятию «центробежной силы». Зададим себе вопрос: куда направится струя воды, если в стенке ведерка сделать отверстие? Не будь силы тяжести, водяная струя по инерции направилась бы по касательной АК к окружности АВ (рис.31). Сила же тяжести заставляет струю снижаться и описывать кривую (параболу) АР. Если круговая скорость достаточно велика, эта кривая расположится вне окружности АВ. Струя обнаруживает перед нами тот путь, по которому при вращении ведерка двигалась бы вода, если бы не препятствовало надавливающее на нее ведерко. Теперь понятно, что вода вовсе не стремится двигаться отвесно вниз, а потому и не выливается из ведерка. Она могла бы вылиться из него лишь в том случае, если бы ведерко было обращено отверстием в направлении его вращения.
Рис.31. Почему не выливается вода из вращаемого ведра?
Вычислите теперь, с какой скоростью надо в этом опыте вращать ведерко, чтобы вода из него не выливалась вниз.
Скорость эта должна быть такова, чтобы центростремительное ускорение вращающегося ведерка было не меньше ускорения свободного падения: тогда путь, по которому стремится двигаться вода, будет лежать вне окружности, описываемой ведерком, и вода нигде от ведерка не отстанет. Формула для вычисления центростремительного ускорения w такова:
где v — круговая скорость, R — радиус кругового пути. Так как ускорение свободного падения на земной поверхности g=9,8 м/с 2 , то имеем неравенство
Если положить R равным 70 см, то
Легко рассчитать, что для получения такой круговой скорости надо делать рукой около полутора оборотов в секунду. Подобная частота вращения вполне достижима, и опыт удается без труда.
Способностью жидкости прижиматься к стенкам сосуда, в котором она вращается вокруг горизонтальной оси, пользуются в технике для так называемого центробежного литья. При этом имеет существенное значение то, что неоднородная жидкость расслаивается по плотности: более тяжелые составные части располагаются дальше от оси вращения, легкие занимают места ближе к оси. Вследствие этого все газы, содержащиеся в расплавленном металле и образующие так называемые «раковины» в литье, выделяются из металла во внутреннюю, полую часть отливки. Изделия, изготовленные таким способом, получаются плотными и свободными от раковин. Центробежное литье дешевле обычного литья под давлением и не требует сложного оборудования.
Источник