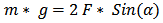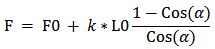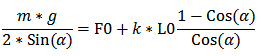Сила натяжения троса под водой

Расчет запаса надежности навесной переправы

Я не собираюсь оспаривать правила и сложившиеся традиции в альпинистской и туристической среде. Если положено переправу делать из сдвоенной основной веревки — значит надо делать так. Соблюдать правила или нет — личное дело каждого (кроме командира группы, ответственного за всех остальных, конечно же). Я выкладываю лишь результаты математических расчетов, которые могут быть интересны любознательным людям.

Условия задачи

Провисание груза на переправе обусловлено растяжением веревки. Предположим, что веревка растягивается не очень сильно, и её удлинение под нагрузкой подчиняется закону Гука.

Ослаблением натяжения веревки за счет затягивания узлов, упругости точек крепления переправы и подобными факторами мы пренебрежем.

Очевидно, что сильнее всего веревка натянута при расположении груза в середине переправы. Ради простоты расчетов мы будем рассматривать только такой случай.

Теория

Рассмотрим силы, действующие на груз, который подвешен в середине переправы. Нас интересует только вертикальная составляющая.

где m*g — сила тяжести, действующая на груз,
F — сила натяжения веревки,
α — угол отклонения веревки от горизонтали.

Сила натяжения веревки, согласно закону Гука, будет подчиняться следующей формуле:

где F0 — сила предварительного натяжения веревки (без груза),
k — коэффициент жесткости веревки,
L0 — длина переправы.

Данных о коэффициенте жесткости альпинистских веревок мне найти не удалось. Пришлось провести эксперимент и порастягивать веревку безменом. Новая 8 мм статика дала значение порядка 2800 Н/м. Точность измерений оставляет желать лучшего, но порядок значений именно такой.

Подставим выражение для силы натяжения в первую формулу, получим следующее:

Получившееся уравнение даже имеет аналитическое решение в области действительных чиссел! 🙂

Нас интересует действительное положительное решение относительно α в окресностях ноля. Я не буду его приводить в аналитическом виде, оно слишком громоздко. Вычислив α, легко получить и все остальные нужные нам параметры.

Расчеты

Входные данные: масса груза, длина переправы, преднатяжение веревки. Нас интересуют натяжение веревки под грузом, максимальное провисание переправы и коэффициент запаса прочности.

Рассмотрим наиболее типичный случай. Переправляем груз массой 80 кг через реку шириной 30 м. Веревка основная, сдвоенная. Гарантированное усилие на разрыв — 44 кН. Жесткость веревки примем за 6000 Н/м (=2*3000 Н/м, т.к. веревка сдвоенная). Поскольку в переправе из сдвоенной веревки каждая из веревок натягивается независимо, то усилие преднатяга также можно сделать вдвое большим, пусть это будет 3000 Н (=2*1500 Н).

Масса груза	80 кг	Максимальное усилие на разрыв	44000 Н
Длина переправы	30 м	Натяжение веревки под грузом	3911 Н
Преднатяжение веревки	3000 Н	Максимальное провисание груза	3.02 м
Коэффициент жесткости веревки	6000 Н/м	Коэффициент запаса прочности	11.25

Что касается провиса переправы, вполне ожидаемый и согласующийся с практикой результат. Даже при условии очень сильного натяжения переправы точки крепления следует располагать повыше над водой. Посмотрим теперь, что будет, если использовать одинарную веревку?

Масса груза	80 кг	Максимальное усилие на разрыв	22000 Н
Длина переправы	30 м	Натяжение веревки под грузом	2568 Н
Преднатяжение веревки	1500 Н	Максимальное провисание груза	4.63 м
Коэффициент жесткости веревки	3000 Н/м	Коэффициент запаса прочности	8.56

Удивительно, но коэффициент запаса прочности изменился не так уж и сильно! Я нахожу объяснение этому в том, что веревка сильнее растягивается.

Выходит, что больший практический смысл использовать двойную веревку в переправе отнюдь не в повышенной надежности, а уменьшении провиса! С надежностью даже в этом случае всё очень-очень хорошо. Считаю, что даже трех- четырехкратного запаса вполне бы хватило, даже учитывая снижение прочности за счет узлов и за счет старения веревки.

Возьмем вариант с одинарной основной веревкой за некий эталон и попробуем изменять другие параметры. Начнем с массы.

Масса груза	50 кг	Максимальное усилие на разрыв	22000 Н
Длина переправы	30 м	Натяжение веревки под грузом	2112 Н
Преднатяжение веревки	1500 Н	Максимальное провисание груза	3.50 м
Коэффициент жесткости веревки	3000 Н/м	Коэффициент запаса прочности	10.4

Уменьшение массы груза в полтора раза разительно снижает провисание переправы.
А что если сократить ширину реки, скажем, до 10 метров?

Масса груза	80 кг	Максимальное усилие на разрыв	22000 Н
Длина переправы	10 м	Натяжение веревки под грузом	2059 Н
Преднатяжение веревки	1500 Н	Максимальное провисание груза	1.94 м
Коэффициент жесткости веревки	3000 Н/м	Коэффициент запаса прочности	10.68

Снова радикальное снижение провисания. Отсюда вывод: если деревья по берегам реки не позволяют закрепить переправу повыше, то есть большой резон искать место, где река сужается!

Наконец, рассмотрим самый жесткий случай: переправляем груз массой 100 кг по переправе длиной 50 м по одинарной веревке, умудрившись натянуть её до состояния струны в 5000 Н.

Масса груза	100 кг	Максимальное усилие на разрыв	22000 Н
Длина переправы	50 м	Натяжение веревки под грузом	5581 Н
Преднатяжение веревки	5000 Н	Максимальное провисание груза	4.40 м
Коэффициент жесткости веревки	3000 Н/м	Коэффициент запаса прочности	3.94

Даже в этом случае коэффициент запаса прочности достаточен для безопасной переправы.

Рассмотрим еще один экстремальный случай. Вместо основной веревки возьмем одинарный 6 мм шнур.

Масса груза	80 кг	Максимальное усилие на разрыв	7200 Н
Длина переправы	30 м	Натяжение веревки под грузом	2568 Н
Преднатяжение веревки	1500 Н	Максимальное провисание груза	4.63 м
Коэффициент жесткости веревки	3000 Н/м	Коэффициент запаса прочности	2.80

Разница с эталонным вариантом — только в максимальном усилии на разрыв веревки, которое в данном случае равно 7200 Н. Коэффициент жесткости примерно такой же (может чуть поменьше будет, но это не дает большого эффекта). Соответственно провис переправы тоже тот же самый. Разница — в коэффициенте запаса прочности, который оказывается равен 2.80. Чисто теоретически должно выдержать. Чисто практически я бы попробовал этот вариант только в самом крайнем, исключительном случае.

Выводы

Использование сдвоенной веревки осмыслено скорее с точки зрения уменьшения провиса переправы. На безопасность сдвоенная веревка влияет только лишь с той позиции, что если одна из веревок порвется, это не приведет к жертвам. Влияние на коэффициент запаса прочности за счет сдваивания минимально. И уж точно коэффициент не отличается в 2 раза, как это могло бы показаться на первый взгляд.

Провис переправы сильно зависит от массы груза.

Длина переправы влияет в основном на провис, а не на максимальное натяжение веревки, хотя определенная зависимость, конечно же, есть. При возможности следует делать переправу как можно короче.

Источник

Учебники

Журнал «Квант»

Общие

Буздин А. И. О швартовке, трении и формуле Эйлера //Квант. — 1988. — № 5. — С. 49-50.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Содержание

Наверное, всем хорошо известно, что при швартовке судна с него бросают на пристань канат (швартов) с петлей на конце, которую надевают на причальную тумбу. Затем, когда судно подходит совсем близко к пристани, матрос быстро наматывает другой конец каната «восьмеркой» на специальную опору на палубе — кнехт (чугунная парная тумба). Таким способом удается надежно удерживать громадное судно рядом с причалом. В чем же здесь дело? В необычайной силе матроса?

По-видимому, многие, в том числе и прославленный писатель-фантаст Жюль Берн, склонны именно к такому заключению. Обратимся, вслед за Перельманом [1] , к эпизоду из книги Жюля Верна «Матиас Шандор», где описывается подвиг силача-атлета Матифу. Этот герой при спуске на воду судна «Трабоколо» предотвратил его столкновение с маленькой прогулочной яхтой, что грозило яхте гибелью.

«. «Трабоколо» быстро скользило вниз по наклону. Белый дымок, появившийся вследствие трения, закрутился перед его носом, тогда как корма погрузилась уже в воду бухты (судно спускалось на воду кормой вперед — А. Б.).

Вдруг появляется человек, схватывает швартов, висящий у передней части «Трабоколо», и старается удержать его, пригнувшись к земле. В одно мгновение он наматывает швартов на вбитую в землю металлическую трубу и, рискуя быть раздавленным, держит с нечеловеческой силой в руках канат в продолжение 10 секунд.»

Жюль Берн правильно отметил роль, которую играет трение во время скольжения корабля,— нагрев его корпуса и возникновение из-за этого дыма. Однако он недооценил роль трения (и переоценил, тем самым, роль Матифу) при описании подвига атлета.

Давайте попробуем разобраться, какая сила нужна, чтобы удержать канат, уже намотанный на опору — трубу или кнехт.

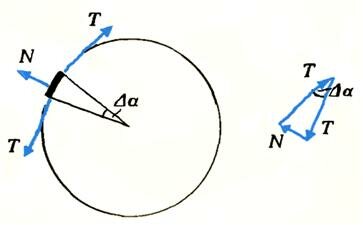
Вначале трением пренебрежем и рассмотрим неподвижный участок каната, изогнутый опорой на малый угол Δα (см. рисунок). Пусть канат натянут силой T и со стороны опоры на рассматриваемый участок каната действует сила реакции N. Найдем ее из условия равновесия каната: сумма всех сил, действующих на участок каната, равна нулю. Отсюда

N = T \Delta \alpha\)

(здесь мы учли, что для малых углов sin Δα = Δα).

При наличии трения канат может быть неподвижным и в том случае, когда силы натяжения слева и справа от рассматриваемого участка немного отличаются друг от друга. Проскальзывание каната начнется тогда, когда разность этих сил достигнет максимальной величины силы трения покоя:

\Delta T = F_ = \mu N = \mu T \Delta \alpha\),

где μ — коэффициент трения между канатом и опорой. Из последнего равенства следует, что скорость изменения силы натяжения каната с ростом угла охвата пропорциональна величине силы натяжения:

Знак минус здесь означает, что при увеличении угла охвата натяжение каната уменьшается.

В физике часто встречаются ситуации, когда скорость изменения какой- либо величины пропорциональна самой этой величине. Напомним, например, явление естественного радиоактивного распада («Физика 10», § 92): уменьшение числа нераспавшихся радиоактивных ядер в единицу времени пропорционально их же числу. Другим примером может служить разряд заряженного конденсатора через резистор: уменьшение заряда на конденсаторе пропорционально току через резистор, который, в свою очередь, пропорционален заряду конденсатора. Во всех этих случаях происходит очень быстрое изменение соответствующей величины. Действительно, если, например, скорость изменения скорости (ускорение) движения тела постоянна, то величина скорости линейно растет со временем. Если же ускорение пропорционально скорости, то оно все время увеличивается и скорость растет намного быстрее — по так называемому экспоненциальному закону.

Такая же зависимость получается и в нашем случае для изменения силы натяжения каната. (Подчеркнем еще раз, что речь идет о минимально возможной разности сил натяжения каната — когда вот-вот начнется его скольжение по опоре.) Впервые этот вопрос был рассмотрен великим математиком, механиком, физиком и астрономом Леонардом Эйлером (1707—1783). Он показал, что натяжение каната Т в зависимости от угла охвата опоры канатом (угол навития) а изменяется по закону

где е = 2,72. — основание натурального логарифма, T₀ — начальное натяжение каната (еще не навитого на опору).

Угол α (измеряемый в радианах) связан с числом оборотов n каната вокруг кнехта простым соотношением: α = 2 πn. Тогда, если при одном обороте натяжение каната уменьшается в k раз, т. е.

после n оборотов натяжение ослабевает в k n раз:

При коэффициенте трения μ = 0,3, например, один оборот каната вокруг кнехта уменьшает силу его натяжения почти в 7 раз, а если сделать два оборота — натяжение ослабевает примерно в 40 раз! С ростом числа оборотов натяжение каната (благодаря трению) становится все меньше и меньше и постепенно сходит на нет.

Возвращаясь к герою Жюля Верна Матифу, мы теперь можем сказать, что, намотав канат на железную трубу, он сильно облегчил себе задачу. Я. И. Перельман, используя содержащиеся в романе данные о «Трабоколо» и сделав соответствующие расчеты, обнаружил, что если силач Матифу успел обернуть канат вокруг трубы три раза, то на его месте мог бы быть и ребенок. Точно так же и при швартовке судов от матросов не требуется большой силы — нужно лишь проявить внимательность и ловкость и вовремя успеть быстро намотать канат на кнехт.

Заметим, что с рассмотренным явлением каждый из вас сталкивается практически ежедневно, что-нибудь завязывая — будь то шнурки, шарф или веревка. Ведь любой узел по существу представляет собой веревку, навитую на «опору» (ту же самую веревку).

Источник