Стакан с водой уравнение

Физика. 8 класс. Перышкин А.В Лабораторная работа №1

Привет, кто поможет горю. Может уже кто делал ?!
Нужна Лабораторная работа №1 Физика. 8 класс. Перышкин А.В

Привет, если у нас одни и теже учебники , то тогда тебе повезло:)
Лабораторная работа 1
Сравнение количеств теплоты при смешивании воды разной температуры
Цель работы: определить количество теплоты, отданное горячей водой и полученное холодной при теплообмене, и объяснить полученный результат.
Приборы и материалы: калориметр, измерительный цилиндр (мензурка), термометр, стакан.
Ход работы:
1. Нальем в калориметр горячей воды массой 100 г. Возьмем столько же холодной воды и нальем ее в стакан. Измерим с помощью термометра температуру холодной и горячей воды. Результаты измерений занесем в таблицу.
2. Вольем холодную воду в калориметр, в сосуд с горячей водой, помешаем термометром и измерим температуру полученной смеси (72°С). Результат измерений занесем в таблицу.
3. Рассчитаем количество теплоты отданное горячей и полученное холодной водой по следующим формулам:

rде: Q — количество теплоты отданное горячей водой; Q1 — количество теплоты полученное холодной водой; m — масса холодной или горячей воды; с = 4200 — теплоемкость воды; t – температура горячей воды; t1 – температура холодной воды; t2 – температура смеси.

Выводы: В результате измерений было установлено, что количество теплоты отданное горячей водой равно количеству теплоты полученное холод­ной водой. Таким образом, подтверждается закон сохранения энергии.

Источник

Почему стакан с водой не может заменить авиагоризонт?

Есть такое поверье, что в случае отказа всех авиагоризонтов можно наполнить стакан водой и лететь по нему. Казалось бы — а почему нет?

Попробуйте поставить стакан с водой на табуретку, представить, что табуретка это козырек приборной панели и понаклонять ее. Работает? Да. Уровень воды будет параллелен полу, а вовсе не сиденью табуретки. Тогда в чем проблема? Метод вполне пригоден? На самом деле — нет. И вот почему:

В первую очередь нам будет мешать самая обычная болтанка. Редко когда мы летаем в идеально спокойной атмосфере, а в остальных случаях. Не будет ровного зеркала воды, которое сможет служить индикатором. Особенно часто, кстати, болтанка присутствует в облачности, то есть именно тогда, когда нам и нужен авиагоризонт. Проводим очередной эксперимент — садимся в обычный автобус, наливаем воду в стакан и смотрим. Если дорога неидеальна (а идеальных дорог нет даже в Москве) абсурдность идеи сразу станет понятна. Вода будет вести себя так, что определить по ней горизонт ну никак не получится, тут штаны бы не облить.

Направление действия силы тяжести в самолете, как это ни странно, не всегда вертикально относительно земли. Для начала разберемся с системами координат — нас интересует так называемая «связанная система координат», она же самолетная. Ось Х этой системы совпадает с продольной осью фюзеляжа, ось У направлена вверх, перпендикулярно СГФ (строительная горизонталь фюзеляжа), а ось Z смотрит вправо. Так вот — в полете направление действия силы тяжести обычно совпадает с осью У связанной системы (с некоторым допуском, разумеется).

Вне зависимости от текущих углов тангажа и крена. Собственно «координированный» разворот тем и отличается от «некоординированного», что в первом случае перегрузка действует строго вдоль оси У, а во втором — как придется.

То есть пока самолет стоит на земле — стакан-авиагоризонт работает правильно — поверхность воды перпендикулярна как оси У земной системы координат (то есть горизонтальна) так и самолетной. Но вот дальше. Мне, честно говоря, лень углубляться в аэродинамику и динамику полета, поэтому снова несколько простых примеров.

Пример 1. Представьте, что мы закрепили наш стакан на баке мотоцикла и едем по идеальной прямой по идеальному асфальту без ускорений. Стакан-авиагоризонт покажет все правильно. Но вот — поворот! Все видели мотоциклы и все видели как они проходят повороты. Так вот — в повороте, при идеальном его выполнении, вода в стакане будет параллельна не поверхности земли, а поверхности бака, на которой установлен наш стакан.

Пример 2. Наверное многие видели мотоциклетные шоу, когда мотоциклисты ездят по вертикальным стенкам цилиндра? Несложно догадаться, что и в этом случае, поверхность воды в стакане будет параллельна стенке цилиндра, а вовсе не земному горизонту. Мотоциклист ведь не падает со стенки только потому, что есть некая сила прижимающая его к ней и действует эта сила именно по нормали (перпендикулярно) к опорной поверхности, то есть стенке цилиндра.

Пример 3. А этот эксперимент многие проводили в детстве. Берем ведро, наливаем воду и начинаем вращать ведро в вертикальной плоскости. И, о чудо, в верхней точки траектории, когда ведро перевернуто, вода вовсе не выливается из него. Вот точно так же будет себя вести и вода в стакане-авиагоризонте, установленном в пилотажном самолете в верхней точке петли.

И снова вернемся в самолет. Самый обычный, пассажирский. Наливаем воду в стакан и ждем начала разбега. Вот заревели двигатели, появилось ускорение. Смотрим в свой стакан, а там. Вода показывает нам увеличение тангажа, хотя мы еще разбегаемся по полосе на трех стойках и тангаж у нас нулевой. То же самое можно повторить и в наземном транспорте в повороте. Машина в повороте кренится минимально, а вот водичка в стакане покажет довольно значительный крен. То есть ускорения, вызванные разгоном, торможением или скольжением самолёта, сделают показания стакана-авиагоризонта абсолютно недостоверными.

И последний, но самый главный эксперимент. Наливаем воду в стакан перед началом захода на посадку. Погода должна быть хорошей, чтобы видеть землю. Во время полета по STAR (схема захода на посадку) иногда приходится покрутиться очень хорошо. Крены легко достигают 30 градусов (пассажирам кажется, что чуть ли не 90!), а вот уровень воды в стакане. Будет по прежнему параллелен полу пассажирского салона, а не естественному горизонту. И это будет очень хорошо видно.

Источник

Капиллярные явления

Введение

В наш век высоких технологий все большее значение в жизни людей имеют естественные науки. Люди 21 века производят супер производительные компьютеры,смартфоны,все глубже и глубже изучают окружающий нас мир. Я думаю, что люди готовятся к новой научно технической революции, которая изменит наше будущее коренным образом. Но когда произойдут эти изменения никто не знает. Каждый человек своим трудом может приблизить этот день.

Эта научно-исследовательская работа – мой маленький вклад в развитие физики.

Данная научно-исследовательская работа посвящена актуальной на данный момент теме «Капиллярные явления». В жизни мы часто имеем дело с телами, пронизанными множеством мелких каналов (бумага, пряжа, кожа, различные строительные материалы, почва, дерево). Приходя в соприкосновение с водой или другими жидкостями, такие тела очень часто впитывают их в себя. В данном проекте показана важность капилляров в жизни живых и неживых организмов.

Цель исследовательской работы: обосновать с точки зрения физики причину движения жидкости по капиллярам, выявить особенности капиллярных явлений.

Объект исследования: свойство жидкостей, всасываясь, подниматься или опускаться по капиллярам.

Предмет исследования: капиллярные явления в живой и неживой природе.

1. Изучить теоретический материал о свойствах жидкости.
2. Ознакомиться с материалом о капиллярных явлениях.
3. Провести серию экспериментов с целью выяснения причины поднятия жидкости в капиллярах.
4. Обобщить изученный в ходе работы материал и сформулировать вывод.

Прежде чем перейти к изучению капиллярных явлений, надо ознакомиться со свойствами жидкости, которые играют немалую роль в капиллярных явлениях.

Поверхностное натяжение

Сам термин «поверхностное натяжение» подразумевает, что вещество у поверхности находится в «натянутом», то есть напряжённом состоянии, которое объясняется действием силы, называемой внутренним давлением. Она стягивает молекулы внутрь жидкости в направлении, перпендикулярном её поверхности. Так, молекулы, находящиеся во внутренних слоях вещества, испытывают в среднем одинаковое по всем направлениям притяжение со стороны окружающих молекул; молекулы же поверхностного слоя подвергаются неодинаковому притяжению со стороны внутренних слоёв веществ и со стороны, граничащей с поверхностным слоем среды. Например, на поверхности раздела жидкость – воздух молекулы жидкости, находящиеся в поверхностном слое, сильнее притягиваются со стороны соседних молекул внутренних слоёв жидкости, чем со стороны молекул воздуха. Это и является причиной различия свойств поверхностного слоя жидкости от свойств её внутренних объёмов.

Внутреннее давление обуславливает втягивание молекул, расположенных на поверхности жидкости, внутрь и тем самым стремится уменьшить поверхность до минимальной при данных условиях. Сила, действующая на единицу длины границы раздела, обуславливающая сокращение поверхности жидкости, называется силой поверхностного натяжения или просто поверхностным натяжением σ .

Поверхностное натяжение различных жидкостей неодинаково, оно зависит от их мольного объёма, полярности молекул, способности молекул к образованию водородной связи между собой и др.

При увеличении температуры поверхностное натяжение уменьшается по линейному закону. На поверхностное натяжение жидкости оказывают влияние и находящиеся в ней примеси. Вещества, ослабляющие поверхностное натяжение, называют поверхностно-активными (ПАВ). По отношению к воде ПАВ являются нефтепродукты, спирты, эфир, мыло и др. жидкие и твёрдые вещества. Некоторые вещества увеличивают поверхностное натяжение. Примеси солей и сахара, например.

Объяснение этому даёт МКТ. Если силы притяжения между молекулами самой жидкости больше сил притяжения между молекулами ПАВ и жидкости, то молекулы жидкости уходят внутрь из поверхностного слоя, а молекулы ПАВ вытесняются на поверхность. Очевидно, что молекулы соли и сахара будут втянуты в жидкость, а молекулы воды вытеснены на поверхность. Таким образом, поверхностное натяжение – основное понятие физики и химии поверхностных явлений – представляет собой одну из наиболее важных характеристик и в практическом отношении. Следует отметить, что всякое серьёзное научное исследование в области физики гетерогенных систем требует измерения поверхностного натяжения. История экспериментальных методов определения поверхностного натяжения, насчитывающая более двух столетий, прошла путь от простых и грубых способов до прецизионных методик, позволяющих находить поверхностное натяжение с точностью до сотых долей процента. Интерес к этой проблеме особенно возрос в последние десятилетия в связи с выходом человека в космос, развитием промышленного строения, где капиллярные силы в различных устройствах часто играют определяющую роль.

Один из таких методов определения поверхностного натяжения основан на поднятии смачивающей жидкости между двумя стеклянными пластинками. Их следует опустить в сосуд с водой и постепенно сближать параллельно друг другу. Вода начнёт подниматься между пластинками – её будет втягивать сила поверхностного натяжения, о которой сказано выше. Легко рассчитать коэффициент поверхностного натяжения σ можно по высоте подъёма воды у и зазору между пластинками d.

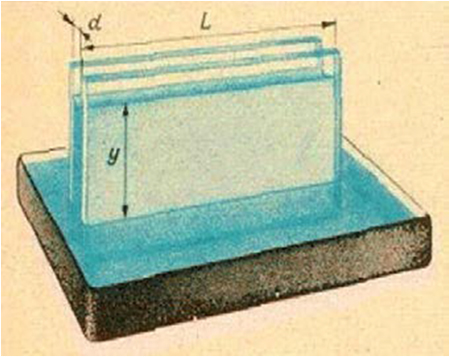
Сила поверхностного натяжения F = 2 σ L, где L – длина пластинки (двойка появилась из-за того, что вода соприкасается с обеими пластинками). Эта сила удерживает слой воды массы m = ρ Ldу, где ρ – плотность воды. Таким образом, 2 σ L = ρ Ldуg. Отсюда можно найти коэффициент поверхностного натяжения σ = 1/2( ρ gdу). (1)Но интереснее сделать так: с одного конца сжать пластинки вместе, а с другого оставить небольшой зазор.

Вода поднимется и образует между пластинками удивительно правильную поверхность. Сечение этой поверхности вертикальной плоскостью – гипербола. Для доказательства достаточно в формулу (1) вместо d подставить новое выражение для зазора в данном месте. Из подобия соответствующих треугольников (см. рис. 2) d = D (x/L). Здесь D – зазор на конце, L – по-прежнему длина пластинки, а x – расстояние от места соприкосновения пластинок до места, где определяется зазор и высота уровня. Таким образом, σ = 1/2( ρ gу)D(x/L), или у = 2 σ L/ ρ gD(1/х). (2)Уравнение (2) действительно является уравнением гиперболы.

Смачивание и несмачивание

Для детального изучения капиллярных явлений следует рассмотреть и некоторые молекулярные явления, обнаруживающиеся на трёхфазной границе сосуществования твёрдой, жидкой, газообразной фаз, в частности рассматривается соприкосновение жидкости с твёрдым телом. Если силы сцепления между молекулами жидкости больше, чем между молекулами твёрдого тела, то жидкость стремится уменьшить границу (площадь) своего соприкосновения с твёрдым телом, по возможности отступая от него. Капля такой жидкости на горизонтальной поверхности твёрдого тела примет форму сплюснутого шара. В этом случае жидкость называется несмачивающей твёрдое тело. Угол θ , образованный поверхностью твёрдого тела и касательной к поверхности жидкости, называется краевым. Для несмачивающей θ > 90°. В этом случае твёрдая поверхность, несмачиваемая жидкостью называется гидрофобной, или олоефильной. Если же силы сцепления между молекулами жидкости меньше, чем между молекулами жидкости и твёрдого тела, то жидкость стремится увеличить границу соприкосновения с твёрдым телом. В этом случае жидкость называется смачивающей твёрдое тело; краевой угол θ 90°. Поверхность же будет носить название гидрофильная. Случай, когда θ = 180°, называется полным несмачиванием. Однако это практически никогда не наблюдается, так как между молекулами жидкости и твёрдого тела всегда действуют силы притяжения. При θ = 0° наблюдается полное смачивание: жидкость растекается по всей поверхности твёрдого тела. Полное смачивание или полное несмачиваение являются крайними случаями. Между ними в зависимости от соотношения молекулярных сил промежуточное положение занимают переходные случаи неполного смачивания.

Смачиваемость и несмачиваемость – понятия относительные: жидкость,смачивающая одно твёрдое тело, может не смачивать другое тело. Например,вода смачивает стекло, но не смачивает парафин; ртуть не смачивает стекло, но смачивает медь.

Смачивание обычно трактуется как результат действия сил поверхностного натяжения. Пусть поверхностное натяжение на границе воздух – жидкость σ 1,2,на границе жидкость – твёрдое тело σ 1,3, на границе воздух – твёрдое тело σ 2,3.

На единицу длины периметра смачивания действуют три силы, численно равные σ 1,2, σ 2,3, σ 1,3, направленные по касательной к соответствующим границам раздела. В случае равновесия все силы должны уравновешивать друг друга. Силы σ 2,3 и σ 1,3 действуют в плоскости поверхности твёрдого тела, сила σ 1,2 направлена к поверхности под углом θ .

Условие равновесия межфазных поверхностей имеет следующий вид: σ 2,3 = σ 1,3 + σ 1,2cos θ или cos θ =( σ 2,3 − σ1 ,3)/ σ 1,2

Величину cos θ принято называть смачиванием и обозначать буквой В.

Определённое влияние на смачивание оказывает состояние поверхности. Смачиваемость резко меняется уже при наличии мономолекулярного слоя углеводородов. Последние же всегда присутствуют в атмосфере в достаточных количествах. Определённое влияние на смачивание оказывает и микрорельеф поверхности. Однако до настоящего времени пока не выявлена единая закономерность влияния шероховатости любой поверхности на смачивание её любой жидкостью. Например уравнение Венцеля-Дерягина cosθ = xcosθ0 связывает краевые углы жидкости на шероховатой ( θ ) и гладкой ( θ 0) поверхностях с отношением х площади истинной поверхности шероховатого тела к её проекции на плоскость. Однако на практике это уравнение не всегда соблюдается. Так, согласно этому уравнению в случае смачивания (θ 90 – к его увеличению (т.е. к большей гидрофобности). Исходя из этого и даются, как правило, сведения о влиянии шероховатости на смачивание.

По мнению многих авторов, скорость растекания жидкости на шероховатой поверхности ниже вследствие того, что жидкость при растекании испытывает задерживающее влияние встречающихся бугорков (гребней) шероховатостей. Необходимо отметить, что именно скорость изменения диаметра пятна, образованного строго дозированной каплей жидкости, нанесённой на чистую поверхность материала, используется в качестве основной характеристики смачивания в капиллярах. Её величина зависит как от поверхностных явлений, так и от вязкости жидкости, её плотности, летучести.

Очевидно, что более вязкая жидкость с прочими одинаковыми свойствами дольше растекается по поверхности и следовательно медленнее протекает по капиллярному каналу.

Капиллярные явления

Капиллярные явления, совокупность явлений, обусловленных поверхностным натяжением на границе раздела несмешивающихся сред (в системах жидкость — жидкость, жидкость — газ или пар) при наличии искривления поверхности. Частный случай поверхностных явлений.

Изучив подробно силы, лежащих в основе капиллярных явлений, стоит перейти непосредственно к капиллярам. Так, опытным путём можно пронаблюдать, что смачивающая жидкость (например, вода в стеклянной трубке) поднимается по капилляру. При этом, чем меньше радиус капилляра, тем на большую высоту поднимается в ней жидкость. Жидкость, не смачивающая стенки капилляра (например, ртуть с стеклянной трубке), опускается ниже уровня жидкости в широком сосуде. Так почему же смачивающая жидкость поднимается по капилляру, а несмачивающая опускается?

Не трудно заметить, что непосредственно у стенок сосуда поверхность жидкости несколько искривлена. Если молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют с молекулами твёрдого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твёрдым телом (смачивающая жидкость). При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится. Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твёрдым телом, её поверхность искривляется вверх. В этом случае говорят о несмачивании жидкостью стенок сосуда.

В узких трубочках, диаметр которых составляет доли миллиметра, искривлённые края жидкости охватывают весь поверхностный слой, и вся поверхность жидкости в таких трубочках имеет вид, напоминающий полусферу. Это так называемый мениск. Он может быть вогнутым, что наблюдается в случае смачивания, и выпуклым при несмачивании. Радиус кривизны поверхности жидкости при этом того же порядка, что и радиус трубки. Явления смачивания и несмачивания в данном случае также характеризуется краевым углом θ между смоченной поверхностью капиллярной трубки и мениском в точках их соприкосновения.

Под вогнутым мениском смачивающей жидкости давление меньше, чем под плоской поверхностью. Поэтому жидкость в узкой трубке (капилляре) поднимается до тех пор, пока гидростатическое давление поднятой в капилляре жидкости на уровне плоской поверхности не скомпенсирует разность давлений. Под выпуклым мениском несмачивающей жидкости давление больше, чем под плоской поверхностью, и это ведёт к опусканию несмачивающей жидкости.

Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа: ∆p = ± 2 σ /R.

Знак капиллярного давления («плюс» или «минус») зависит от знака кривизны. Центр кривизны выпуклой поверхности находится внутри соответствующей фазы. Выпуклые поверхности имеют положительную кривизну, вогнутые – отрицательную.

Так, условие равновесия жидкости в капиллярной трубочке определяется равенством

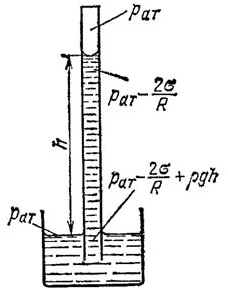
где ρ – плотность жидкости, h – высота её поднятия в трубочке, p₀ – атмосферное давление.

Из данного выражения следует, что h = 2 σ / ρ gR. (2)

Преобразуем полученную формулу, выразив радиус кривизны R мениска через радиус капиллярной трубочки r.

Из рис. 6.18 следует, что r = Rcos θ . Подставляя (1) в (2), получаем: h = 2 σ cos θ / ρ gr.

Полученная формула, определяющая высоту поднятия жидкости в капиллярной трубочке, носит название формулы Жюрена. Очевидно, что чем меньше радиус трубки, тем на большую высоту поднимается в ней жидкость. Кроме того, высота поднятия растёт с увеличением коэффициента поверхностного натяжения жидкости.

Подъём смачивающей жидкости по капилляру можно объяснить и по-другому. Как было сказано ранее, под действием сил поверхностного натяжения поверхность жидкости стремится сократиться. Вследствие этого поверхность вогнутого мениска стремится выпрямиться и сделаться плоской. При этом она тянет за собой частицы жидкости, лежащие под ней, и жидкость поднимается по капилляру вверх. Но поверхность жидкости в узкой трубке плоской оставаться не может, она должна иметь форму вогнутого мениска. Как только в новом положении данная поверхность примет форму мениска, она снова будет стремиться сократиться и т.д. В результате действия этих причин смачивающая жидкость и поднимается по капилляру. Поднятие прекратится, когда сила тяжести Fтяж поднятого столба жидкости, которая тянет поверхность вниз, уравновесит равнодействующую силу F сил поверхностного натяжения, направленных касательно к каждой точке поверхности.

По окружности соприкосновения поверхности жидкости со стенкой капилляра действует сила поверхностного натяжения, равная произведению коэффициента поверхностного натяжения на длину окружности: 2 σπ r, где r – радиус капилляра.

Сила тяжести, действующая на поднятую жидкость,

где ρ – плотность жидкости; h – высота столба жидкости в капилляре; g – устроение силы тяжести.

Подъём жидкости прекращается, когда F_тяж = F или ρπ r^2hg = 2 σπ r. Отсюда высота поднятия жидкости в капилляре h = 2 σ / ρ gR.

В случае несмачивающей жидкости последняя, стремясь сократить свою поверхность, будет опускаться вниз, выталкивая жидкость из капилляра.

Выведенная формула применима и для несмачивающей жидкости. В этом случае h – высота опускания жидкости в капилляре.

Капиллярные явления в природе

Капиллярные явления также весьма распространены в природе и часто используются в практической деятельности человека. Дерево, бумага, кожа, кирпич и очень многие другие предметы, окружающие нас, имеют капилляры. За счет капилляров вода поднимается по стеблям растений и впитывается в полотенце, когда мы им вытираемся. Поднятие воды по мельчайшим отверстиям в куске сахара, забор крови из пальца – это тоже примеры капиллярных явлений.

Кровеносная система человека, начинаясь с весьма толстых сосудов, заканчивается очень разветвленной сетью тончайших капилляров. Могут вызвать интерес, например, такие данные. Площадь поперечного сечения аорты равна 8 см 2 . Диаметр же кровеносного капилляра может быть в 50 раз меньше диаметра человеческого волоса при длине 0,5 мм. В теле взрослого человека имеется порядка 160 млрд капилляров. Их общая длина доходит до 80 тыс. км.

По многочисленным капиллярам, имеющимся в почве, вода из глубинных слоев поднимается к поверхности и интенсивно испаряется. Чтобы замедлить процесс потери влаги, капилляры разрушают путем разрыхления почвы с помощью борон, культиваторов, рыхлителей.

Практическая часть

Возьмем стеклянную трубочку с очень маленьким внутренним диаметром (d

Источник