Теплоизолированный сосуд был до краев наполнен водой

Масса воды, первоначально имевшейся в сосуде, равна, очевидно, 200 г. Кусок льда, опущенный в воду, останется плавать на её поверхности. Поэтому масса вытесненной воды равна массе льда. В результате, в сосуде останется вода массой $m = 200 г — 42 г = 158 г$. Определим, сможет ли оставшаяся вода растопить весь лёд. Для этого вычислим теплоту $Q_<1>$, необходимую для плавления всего куска льда, и теплоту $Q_<2>$, которая выделится при остывании воды до $0^ < \circ>С$:

$Q_ <1>= \lambda m_ <льда>= 330000 \frac<Дж> <кг>\cdot 0,042 кг = 13860 Дж$,
$Q_ <2>= cm \cdot 20^ < \circ>С = 4200 \frac<Дж> C > 0,158 кг \cdot 20^ < \circ>С = 13272 Дж$.

Так как $Q_ <1>> Q_<2>$, то лёд растает не весь, и установившаяся в сосуде температура будет равна $0^ < \circ>С$.

Источник

Всероссийской олимпиады школьников по физике

Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 1

Мартышка и удав движутся навстречу по круговой дорожке, длина которой в два раза больше длины удава. Мартышка бежит со скоростью u по земле, а, встретившись с удавом, заскакивает на него и бежит по нему со скоростью u относительно удава. Добежав до хвоста, она спрыгивает на землю и бежит с той же скоростью u относительно земли. Найдите скорость удава, если после встречи с мартышкой в точке A дорожки следующая встреча произошла в диаметрально противоположной точке B. Удав всё время движется с постоянной скоростью по земле.

Решение: Мартышка добежит до хвоста удава за время t₁ = L/u, где L длина удава (1 балл). Голова удава за это время сместится от A на

x = vt₁ = vL/u (2 балла), на такое же расстояние сместится хвост удава от B (1 балл). Поэтому до места следующей встречи мартышке нужно пробежать по земле расстояние x, а голове удава за то же время t пройти расстояние L – x (1 балл), тогда t = x/u = (L – x)/v (1 балл). Отсюда для скорости удава получим уравнение v 2 = (u – v)u (2 балла), положительный корень которого даёт искомое значение v = u(Ö5 – 1)/2, а отрицательный противоречит условию встречного движения (2 балла).

Ответ: v = u(Ö5 – 1)/2.

Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 2

Имеются два кубика одинакового размера из разных материалов. В сосуд налита вода, а сверху масло плотности ρ = 0,8ρ_о, где ρ_о плотность воды. При опускании в сосуд первого кубика он плавает на границе раздела жидкостей, находясь наполовину объёма в воде и наполовину – в масле. Если кубики склеить и опустить в сосуд, то они плавают полностью погрузившись в воду. Выразите плотности материалов кубиков через плотность воды.

Решение:

Для плавания первого кубика из закона Архимеда следует, что масса кубика равна массе вытесненной жидкости (1 балл).

Выразим массу кубика через его плотность и объём m = ρ₁V (1 балл).

Выразим суммарную массу вытесненной жидкости, учтя равенство вытесненных объёмов воды и масла m = ρV/2 + ρ_oV/2 (2 балла).

В случае плавания склеенных кубиков в воде из закона Архимеда имеем ρ₁V + ρ₂V = 2ρ_oV (2 балла).

Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 3

В электрочайнике с двумя нагревателями необходимо нагреть объем воды от комнатной температуры до температуры кипения. Каждый нагреватель, включенный в сеть отдельно, выделяет мощность . Через какое время закипит вода, если ее подогревать одним нагревателем или двумя, включенными в ту же сеть последовательно или параллельно друг к другу? КПД нагревателя . Удельная теплоемкость воды .

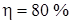
Решение: Для нагреванияводы до температуры кипения необходимо количество теплоты , где – масса воды в чайнике. При включении одного нагревателя его мощность , где – ток, текущий через него, и – напряжение сети. В этом случае на нагревание воды идет часть теплоты, выделяемой нагревателем, ; отсюда время нагревания воды одним нагревателем .

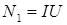
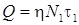
При параллельном включении двух нагревателей, как и при включении одного из них, на каждом нагревателе будет напряжение сети . Следовательно, в каждом из них будет выделяться та же мощность и общая мощность будет ; отсюда время нагревания воды двумя нагревателями .

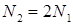
При последовательном включении нагревателей общий ток через них будет равен 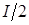. Поэтому общая мощность, выделяемая в них, . Следовательно, время нагревания водя в этом случае .

Ответ: ; ; .

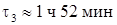
Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 4

Теплоизолированный сосуд был до краев наполнен водой при температуре t₀ = 19 ◦ С. В середину этого сосуда быстро, но аккуратно опустили деталь, изготовленную из металла плотностью ρ₁ = 2700 кг/м 3 , нагретую до температуры t_д = 99 ◦ С, и закрыли крышкой. После установления теплового равновесия температура воды в сосуде равна t_x = 32,2 ◦ С. Затем в этот же сосуд, наполненный до краев водой при температуре t₀ = 19 ◦ С, вновь быстро, но аккуратно опустили две такие же детали, нагретые до той же температуры t_д = 99 ◦ С, и закрыли крышкой. В этом случае после установления в сосуде теплового равновесия температура воды равна

t_y=48,8 ◦ С. Чему равна удельная теплоемкость c₁ металла, из которого изготовлены детали? Плотность воды ρ₀ = 1000 кг/м 3 . Удельная теплоемкость воды с₀ = 4200Дж/(кг ◦ С).

Решение:

Пусть объем сосуда равен V₀, а объем детали — V₁.

Запишем уравнения теплового баланса для первого и для второго случаев:

Исключим из этой системы объем V₀. Для этого выразим в каждом уравнении величину c₀ρ₀V₀ и приравняем получившиеся выражения:

(3)

Объём V₁ сократится. После алгебраических преобразований получим ответ:

(4) (3 балла)

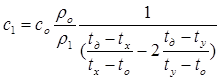
c₁ = 920 Дж/(кг∙ ◦ С) (1 балл).

Ответ: c₁ = 920 Дж/(кг∙ ◦ С).

Муниципальный этап

Дата добавления: 2019-01-14 ; просмотров: 714 ; Мы поможем в написании вашей работы!

Источник

Всероссийской олимпиады школьников по физике

Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 1

Мартышка и удав движутся навстречу по круговой дорожке, длина которой в два раза больше длины удава. Мартышка бежит со скоростью u по земле, а, встретившись с удавом, заскакивает на него и бежит по нему со скоростью u относительно удава. Добежав до хвоста, она спрыгивает на землю и бежит с той же скоростью u относительно земли. Найдите скорость удава, если после встречи с мартышкой в точке A дорожки следующая встреча произошла в диаметрально противоположной точке B. Удав всё время движется с постоянной скоростью по земле.

Решение: Мартышка добежит до хвоста удава за время t₁ = L/u, где L длина удава (1 балл). Голова удава за это время сместится от A на

x = vt₁ = vL/u (2 балла), на такое же расстояние сместится хвост удава от B (1 балл). Поэтому до места следующей встречи мартышке нужно пробежать по земле расстояние x, а голове удава за то же время t пройти расстояние L – x (1 балл), тогда t = x/u = (L – x)/v (1 балл). Отсюда для скорости удава получим уравнение v 2 = (u – v)u (2 балла), положительный корень которого даёт искомое значение v = u(Ö5 – 1)/2, а отрицательный противоречит условию встречного движения (2 балла).

Ответ: v = u(Ö5 – 1)/2.

Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 2

Имеются два кубика одинакового размера из разных материалов. В сосуд налита вода, а сверху масло плотности ρ = 0,8ρ_о, где ρ_о плотность воды. При опускании в сосуд первого кубика он плавает на границе раздела жидкостей, находясь наполовину объёма в воде и наполовину – в масле. Если кубики склеить и опустить в сосуд, то они плавают полностью погрузившись в воду. Выразите плотности материалов кубиков через плотность воды.

Решение:

Для плавания первого кубика из закона Архимеда следует, что масса кубика равна массе вытесненной жидкости (1 балл).

Выразим массу кубика через его плотность и объём m = ρ₁V (1 балл).

Выразим суммарную массу вытесненной жидкости, учтя равенство вытесненных объёмов воды и масла m = ρV/2 + ρ_oV/2 (2 балла).

В случае плавания склеенных кубиков в воде из закона Архимеда имеем ρ₁V + ρ₂V = 2ρ_oV (2 балла).

Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 3

В электрочайнике с двумя нагревателями необходимо нагреть объем воды от комнатной температуры до температуры кипения. Каждый нагреватель, включенный в сеть отдельно, выделяет мощность . Через какое время закипит вода, если ее подогревать одним нагревателем или двумя, включенными в ту же сеть последовательно или параллельно друг к другу? КПД нагревателя . Удельная теплоемкость воды .

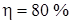
Решение: Для нагреванияводы до температуры кипения необходимо количество теплоты , где – масса воды в чайнике. При включении одного нагревателя его мощность , где – ток, текущий через него, и – напряжение сети. В этом случае на нагревание воды идет часть теплоты, выделяемой нагревателем, ; отсюда время нагревания воды одним нагревателем .

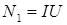
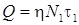
При параллельном включении двух нагревателей, как и при включении одного из них, на каждом нагревателе будет напряжение сети . Следовательно, в каждом из них будет выделяться та же мощность и общая мощность будет ; отсюда время нагревания воды двумя нагревателями .

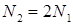
При последовательном включении нагревателей общий ток через них будет равен 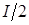. Поэтому общая мощность, выделяемая в них, . Следовательно, время нагревания водя в этом случае .

Ответ: ; ; .

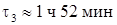
Муниципальный этап

Всероссийской олимпиады школьников по физике

Класс

Учебный год

Задача № 4

Теплоизолированный сосуд был до краев наполнен водой при температуре t₀ = 19 ◦ С. В середину этого сосуда быстро, но аккуратно опустили деталь, изготовленную из металла плотностью ρ₁ = 2700 кг/м 3 , нагретую до температуры t_д = 99 ◦ С, и закрыли крышкой. После установления теплового равновесия температура воды в сосуде равна t_x = 32,2 ◦ С. Затем в этот же сосуд, наполненный до краев водой при температуре t₀ = 19 ◦ С, вновь быстро, но аккуратно опустили две такие же детали, нагретые до той же температуры t_д = 99 ◦ С, и закрыли крышкой. В этом случае после установления в сосуде теплового равновесия температура воды равна

t_y=48,8 ◦ С. Чему равна удельная теплоемкость c₁ металла, из которого изготовлены детали? Плотность воды ρ₀ = 1000 кг/м 3 . Удельная теплоемкость воды с₀ = 4200Дж/(кг ◦ С).

Решение:

Пусть объем сосуда равен V₀, а объем детали — V₁.

Запишем уравнения теплового баланса для первого и для второго случаев:

Исключим из этой системы объем V₀. Для этого выразим в каждом уравнении величину c₀ρ₀V₀ и приравняем получившиеся выражения:

(3)

Объём V₁ сократится. После алгебраических преобразований получим ответ:

(4) (3 балла)

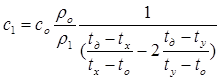
c₁ = 920 Дж/(кг∙ ◦ С) (1 балл).

Ответ: c₁ = 920 Дж/(кг∙ ◦ С).

Муниципальный этап

Дата добавления: 2019-01-14 ; просмотров: 715 ; Мы поможем в написании вашей работы!

Источник