ПРОВЕРКА СТЕРИЛИЗУЮЩИХ ФИЛЬТРОВ НА ЦЕЛОСТНОСТЬ
Проверка стерилизующих фильтров на целостность
Стерилизующая фильтрация газов и жидкостей существует на любом фармацевтическом предприятии. В соответствии с требованиями GMP при использовании систем фильтрации в технологических процессах предприятия необходимо проверять стерилизующие фильтры на целостность. Правила GMP рекомендуют проверять стерилизующие системы фильтрации до начала работы и требуют обязательной проверки на целостность после завершения процесса фильтрации. Таким образом, исключается возможность получения некачественного продукта из-за дефекта стерилизующей мембраны фильтра.
Для этих целей компанией Donaldson Ultrafilter разработан и производится прибор для диагностики целостности фильтров Membra-Check it-01. Прибор позволяет тестировать гидрофильные и гидрофобные фильтры, установленные в фильтродержатель, или капсульные фильтры, а при использовании специальной приставки поверять манометры на точность измерения.
Прибор и программное обеспечение полностью соответствует требованиям FDA и международным стандартам, предъявляемым к электронной измерительной технике. Прибор позволяет проводить следующие тесты:
— тест потери давления
— совместный диффузионный и тест на «точку пузырька»
— диффузионный тест с автоматическим смачиванием фильтра
— водо-интрузионный тест на корпусах большого объема (свыше 150л)
— водо-интрузионный тест с автоматической сушкой фильтра
— водо-интрузионный тест с предварительным охлаждением фильтра после стерилизации
— определения объема сосудов от 0,1 до 32 л
Проверка фильтров на целостность основана на физических явлениях, связанных с процессом взаимодействия смачивающей жидкости и мембраной фильтра.
Диффузионный тест основан на диффузии сжатого газа через смоченную мембрану фильтроэлемента. При этом сжатый воздух растворяется в жидкости, находящейся в порах мембраны, и выходит на обратной стороне фильтра. Под величиной диффузии понимается определенный заданный объем газа, который необходим для компенсации потерь газа вследствии диффузии для поддержания постоянного давления. В поврежденном фильтре величина диффузии значительно превышает заданный параметр на данный тип фильтра. В качестве смачивающей жидкости для гидрофильных фильтров применяется вода, а для гидрофобных — органические растворители (этиловый или изопропиловый спирты) или их смесь с водой. В качестве тестирующего газа используется сжатый воздух или азот.
Тест потери давления проверяет герметичность фильтрационной системы по потере давления за определенный промежуток времени.
Тест на точку пузырька подразумевает плавное повышение давления в системе до образования постоянного воздушного потока. Давление, при котором происходит выдавливание воды из поры фильтра и образование постоянного воздушного потока, называется точкой пузырька.
В ходе водо-интрузионного теста происходит заполнение колокола гидрофобного сухого фильтра водой и подачей сжатого воздуха. При этом измеряется объем воды, который проникает в поры гидрофобного фильтра. Если объем воды не превышает определенного значения, то фильтр прошел проверку на целостность.
Проведение тестов не нарушает стерильность фильтроэлемента, и после проведения теста фильтрационная система полностью готова к работе.
Прибор Membra-Check it-01 может хранить в своей памяти до 100 тестовых программ, и оператору только требуется выбрать нужную, а прибор в автоматическом режиме проведет тест. Небольшие габариты и вес позволяют использовать прибор на всем предприятии, а встроенный принтер и автономное питание позволяют получать результаты испытаний непосредственно на месте.
При необходимости все пневматические линии прибора могут быть промыты горячей водой (до 85 0 С) или моющими средствами, а датчик давления простерилизован в автоклаве.
Прибор изначально комплектуется необходимыми переходниками и адаптерами для подключения к любым типам фильтродежателей. Для проведения тестов небольших фильтров прибор оснащен специальным держателем, который позволяет проводить тесты даже на насадках для шприца.
Для внесения изменений в тестовые программы используется компактная клавиатура, или прибор непосредственно подключается к ПК, на который можно перенести результаты измерений или добавить тестовые программы. Программное обеспечение просто и удобно в работе.
Компания ООО «Далва Консалтинг» является официальным представительством Donaldson Ultrafilter и осуществляет поставки фильтрационного оборудования на территории РФ. При поставке прибора Membra-Check it-01 персонал предприятия проходит обязательное обучение работе с прибором.
Источник
Точка пузырька по воде
Точка пузырька – это минимальное давление газа, необходимое для выдавливания жидкости из пор максимального диаметра мембраны.
Метод «точка пузырька» был разработан Бехольдом в начале века. 
Он основан на эффекте капиллярности (см. Рис.1), согласно которому, высота столбика воды в капилляре обратно пропорциональна диаметру последнему. Вода удерживается в капилляре силами поверхностного натяжения и, если диаметр капилляра уменьшится, высота столба воды возрастет. Однако воду, поднявшуюся в капилляре до определенной высоты, можно вернуть вниз давлением, величина которого эквивалентна высоте столбика воды в капилляре. Следовательно, измеряя давление, при котором вода вытесняется из капилляра, можно вычислить его диаметр.
Применительно к мембране это будет выглядеть следующим образом: Верхняя часть мембраны находится в контакте с жидкостью, которая заполняет все поры мембраны, если выполняется условие смачивания. Нижняя часть мембраны контактирует с воздухом (газом), и при постепенном увеличении давления воздуха пузырек воздуха будет проникать через пору (при выполнении условия равенства радиуса пузырька радиусу поры) (см. Рис.2). Т.е. мембранный фильтр, насыщенный жидкостью, не пропускает воздуха (газа) при тех давлениях, которые обеспечивают его фильтрование через сухой фильтр (диффузионное течение газа). Однако при увеличении давления достигается состояние, при котором сила поверхностного натяжения в больших порах преодолевается, и жидкость из этих пор выталкивается (объемное течение газа) (см.Рис.3). Суть метода состоит в измерении давления, необходимого для проскока воздуха через мембрану (начала объемного течения газа), заполненную жидкостью, которая по отношению к ней является смачивающей. Надо отметить, что проскок газа через смоченную мембрану будет наблюдаться в первую очередь через самые крупные поры, радиус которых можно рассчитать по уравнению Лапласа:
D = 4∙γ ∙(cos θ) / P, (1)
где D – диаметр поры, имеющей форму капилляра (мкм),
γ – поверхностное натяжение на границе жидкость – воздух (для воды 72 дин/см)
θ – краевой угол смачивания (момент проскока газа означает, что контактный угол
θ равен нулю (соs θ = 1))
Р – точка пузырька.
Т.е. в случае воды это уравнение приобретает вид:
D = 221,3 / Р,
где Р – измеряется в см рт.ст.
Из формулы (1) следует, что метод точки пузырька не зависит от природы применяемой жидкости. Однако известно, что при определении пор в одной и той же мембране с использованием различных смачивающих жидкостей: воды, метанола, этанола, н-пропанола, изопропанола дает различные результаты. Явление это малоизучено, вероятно это связано с эффектами смачивания. Поэтому были выбраны еще несколько стандартных смачивающих жидкостей.
В случае измерения очень мелких пор, если в качестве смачивающей среды используется вода, давление, при котором достигается точка пузырька, может быть настолько большим, что происходит деформация мембраны, что сделает результаты измерения недействительными. Поэтому для получения достоверных результатов измерения следует применять жидкости, у которых поверхностное натяжение меньше, чем у воды. Наиболее распространенным в этом случае является минеральное масло со значением поверхностного натяжения 34,7 дин/см. В этом случае уравнение Лапласа принимает вид:
D = 106 / Р
где Р – измеряется в см рт.ст.
Для мембран с еще меньшим размером пор используют еще одну смачивающую жидкость – изобутанол. Сила поверхностного натяжения изобутанола составляет 1,7 дин/см, что позволяет измерять поры в 40 раз меньше, чем это позволяет сделать смачивание водой. Однако в этом случае необходимо убедиться в том, что материал мембраны химически совместим с изобутанолом.
Строго говоря, все выше представленные рассуждения и формулы для определения размера пор методом пузырька справедливы лишь в том случае, если пора имеет цилиндрическую форму. На практике же чаще встречаются мембраны, у которых извилистая пористая структура. Мало того, в большинстве случаев сечение пор больше напоминает эллипс, а не круг.
Возникает вопрос: А чему же тогда соответствуют обозначения размеров пор, проставляемые фирмами-изготовителями мембран, ведь при массовом производстве мембран их размер пор не измеряют, а рассчитывают с помощью математических моделей, основанных на теории капиллярности. Т.е. возникает дилемма. Размеры фильтрующихся частиц мы измеряем непосредственно – под микроскопом, а точка пузырька определяется косвенно из гидродинамики. И, тем не менее, практически все производители указывают точный размер пор мембран.
Поскольку форма поры оказывает существенное влияние на измеренное значение давления точки пузырька производители мембран пускаются на всякого рода «выдумки». А именно в числитель нашего исходного выражения (1) вводят некую поправку, учитывающую форму пор. Назовем эту поправку k. Обычно фирмы-изготовители не приводят то, каким образом получается этот коэффициент, однако известно, что обычно он получается опытным путем для каждого типа мембран.
А можно ли теоритически получить выражение, связывающее точку пузырька и размер некруглой поры? Оказывается, да.
Исходными данными нам будет служить то, что в нашем случае измерения точки пузырька участвуют две противоположно направленные силы: первая (положительная) – сила поверхностного натяжения; вторая (отрицательная) – гидростатическая. Первая, как известно, связана с габаритами поры (периметром) через коэффициент поверхностного натяжения и краевой угол смачивания. Вторая – через прилагаемое усилие (давление газа). В точке пузырька эти противодействующие силы равны. Т.е. можно записать, что:
(периметр сечения поры) · γ ∙ cos θ = (площадь сечения поры) ∙ Р (2)
Как известно из геометрии, эллипс имеет две оси (см. рисунок) – малую (b) и большую (a). При этом именно от первой зависит размер частиц, которые смогут пройти через мембрану. Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи: (S = π · a · b). Если мы обозначим (по аналогии с круглой порой двойную длину полуоси b через D, а двойную длину полуоси a через D1), а соотношение D1 к D через Е, то формулу для вычисления площади эллипса можно записать следующим образом:
S = π · (D1/2) · (D/2) = π · (D · E/2) · (D /2) = (π · D2 · E)/4
В случае круга Е = 1, и мы получим из приведенной выше формулы – формулу для вычисления площади круга.
Аналогичные рассуждения, выполненные применительно к формуле для приблизительного вычисления периметра эллипса, нам дадут следующее выражение:
L = π · D2 · [(1+E2)/2]1/2
Подставив полученные формулы в наше выражение (2) и преобразовав его таким образом, чтобы можно было сравнить результат с формулой (1), мы видим, что уравнение для определения диаметра поры при эллиптическом сечении поры имеет вид:
И опять же в случае круга Е = 1, и мы получим из приведенной выше формулы уравнение (1).
Из этого выражения следует, что размер поры, вычисленный из предположения, что она имеет круглое сечение, будет всегда больше, чем пора эллиптического сечения на 25 – 30%. Поэтому если нам при решении задачи микрофильтрации нам требуется гарантированная степень стерилизации, а не высокая точность классификации мембран по размерам, то, по-видимому, можно пренебречь геометрией пор и сделать допущение о том, что они имеют круглое сечение.
А поскольку точно определить геометрию пор можно только после дополнительных трудоемких исследований, то используя простой метод точки пузырька для определения размера пор мембраны, мы имеем дополнительный фактор безопасности.
Источник
Точка пузырька по воде
Точка пузырька – это минимальное давление газа, необходимое для выдавливания жидкости из пор максимального диаметра мембраны.
Метод «точка пузырька» был разработан Бехольдом в начале века.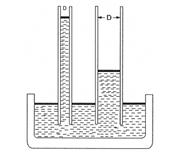 
Он основан на эффекте капиллярности (см. Рис.1), согласно которому, высота столбика воды в капилляре обратно пропорциональна диаметру последнему. Вода удерживается в капилляре силами поверхностного натяжения и, если диаметр капилляра уменьшится, высота столба воды возрастет. Однако воду, поднявшуюся в капилляре до определенной высоты, можно вернуть вниз давлением, величина которого эквивалентна высоте столбика воды в капилляре. Следовательно, измеряя давление, при котором вода вытесняется из капилляра, можно вычислить его диаметр.
Применительно к мембране это будет выглядеть следующим образом: Верхняя часть мембраны находится в контакте с жидкостью, которая заполняет все поры мембраны, если выполняется условие смачивания. Нижняя часть мембраны контактирует с воздухом (газом), и при постепенном увеличении давления воздуха пузырек воздуха будет проникать через пору (при выполнении условия равенства радиуса пузырька радиусу поры) (см. Рис.2). Т.е. мембранный фильтр, насыщенный жидкостью, не пропускает воздуха (газа) при тех давлениях, которые обеспечивают его фильтрование через сухой фильтр (диффузионное течение газа). Однако при увеличении давления достигается состояние, при котором сила поверхностного натяжения в больших порах преодолевается, и жидкость из этих пор выталкивается (объемное течение газа) (см.Рис.3). Суть метода состоит в измерении давления, необходимого для проскока воздуха через мембрану (начала объемного течения газа), заполненную жидкостью, которая по отношению к ней является смачивающей. Надо отметить, что проскок газа через смоченную мембрану будет наблюдаться в первую очередь через самые крупные поры, радиус которых можно рассчитать по уравнению Лапласа:
D = 4∙γ ∙(cos θ) / P, (1)
где D – диаметр поры, имеющей форму капилляра (мкм),
γ – поверхностное натяжение на границе жидкость – воздух (для воды 72 дин/см)
θ – краевой угол смачивания (момент проскока газа означает, что контактный угол
θ равен нулю (соs θ = 1))
Р – точка пузырька.
Т.е. в случае воды это уравнение приобретает вид:
D = 221,3 / Р,
где Р – измеряется в см рт.ст.
Из формулы (1) следует, что метод точки пузырька не зависит от природы применяемой жидкости. Однако известно, что при определении пор в одной и той же мембране с использованием различных смачивающих жидкостей: воды, метанола, этанола, н-пропанола, изопропанола дает различные результаты. Явление это малоизучено, вероятно это связано с эффектами смачивания. Поэтому были выбраны еще несколько стандартных смачивающих жидкостей.
В случае измерения очень мелких пор, если в качестве смачивающей среды используется вода, давление, при котором достигается точка пузырька, может быть настолько большим, что происходит деформация мембраны, что сделает результаты измерения недействительными. Поэтому для получения достоверных результатов измерения следует применять жидкости, у которых поверхностное натяжение меньше, чем у воды. Наиболее распространенным в этом случае является минеральное масло со значением поверхностного натяжения 34,7 дин/см. В этом случае уравнение Лапласа принимает вид:
D = 106 / Р
где Р – измеряется в см рт.ст.
Для мембран с еще меньшим размером пор используют еще одну смачивающую жидкость – изобутанол. Сила поверхностного натяжения изобутанола составляет 1,7 дин/см, что позволяет измерять поры в 40 раз меньше, чем это позволяет сделать смачивание водой. Однако в этом случае необходимо убедиться в том, что материал мембраны химически совместим с изобутанолом.
Строго говоря, все выше представленные рассуждения и формулы для определения размера пор методом пузырька справедливы лишь в том случае, если пора имеет цилиндрическую форму. На практике же чаще встречаются мембраны, у которых извилистая пористая структура. Мало того, в большинстве случаев сечение пор больше напоминает эллипс, а не круг.
Возникает вопрос: А чему же тогда соответствуют обозначения размеров пор, проставляемые фирмами-изготовителями мембран, ведь при массовом производстве мембран их размер пор не измеряют, а рассчитывают с помощью математических моделей, основанных на теории капиллярности. Т.е. возникает дилемма. Размеры фильтрующихся частиц мы измеряем непосредственно – под микроскопом, а точка пузырька определяется косвенно из гидродинамики. И, тем не менее, практически все производители указывают точный размер пор мембран.
Поскольку форма поры оказывает существенное влияние на измеренное значение давления точки пузырька производители мембран пускаются на всякого рода «выдумки». А именно в числитель нашего исходного выражения (1) вводят некую поправку, учитывающую форму пор. Назовем эту поправку k. Обычно фирмы-изготовители не приводят то, каким образом получается этот коэффициент, однако известно, что обычно он получается опытным путем для каждого типа мембран.
А можно ли теоритически получить выражение, связывающее точку пузырька и размер некруглой поры? Оказывается, да.
Исходными данными нам будет служить то, что в нашем случае измерения точки пузырька участвуют две противоположно направленные силы: первая (положительная) – сила поверхностного натяжения; вторая (отрицательная) – гидростатическая. Первая, как известно, связана с габаритами поры (периметром) через коэффициент поверхностного натяжения и краевой угол смачивания. Вторая – через прилагаемое усилие (давление газа). В точке пузырька эти противодействующие силы равны. Т.е. можно записать, что:
(периметр сечения поры) · γ ∙ cos θ = (площадь сечения поры) ∙ Р (2)
Как известно из геометрии, эллипс имеет две оси (см. рисунок) – малую (b) и большую (a). При этом именно от первой зависит размер частиц, которые смогут пройти через мембрану. Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи: (S = π · a · b). Если мы обозначим (по аналогии с круглой порой двойную длину полуоси b через D, а двойную длину полуоси a через D1), а соотношение D1 к D через Е, то формулу для вычисления площади эллипса можно записать следующим образом:
S = π · (D1/2) · (D/2) = π · (D · E/2) · (D /2) = (π · D2 · E)/4
В случае круга Е = 1, и мы получим из приведенной выше формулы – формулу для вычисления площади круга.
Аналогичные рассуждения, выполненные применительно к формуле для приблизительного вычисления периметра эллипса, нам дадут следующее выражение:
L = π · D2 · [(1+E2)/2]1/2
Подставив полученные формулы в наше выражение (2) и преобразовав его таким образом, чтобы можно было сравнить результат с формулой (1), мы видим, что уравнение для определения диаметра поры при эллиптическом сечении поры имеет вид:
И опять же в случае круга Е = 1, и мы получим из приведенной выше формулы уравнение (1).
Из этого выражения следует, что размер поры, вычисленный из предположения, что она имеет круглое сечение, будет всегда больше, чем пора эллиптического сечения на 25 – 30%. Поэтому если нам при решении задачи микрофильтрации нам требуется гарантированная степень стерилизации, а не высокая точность классификации мембран по размерам, то, по-видимому, можно пренебречь геометрией пор и сделать допущение о том, что они имеют круглое сечение.
А поскольку точно определить геометрию пор можно только после дополнительных трудоемких исследований, то используя простой метод точки пузырька для определения размера пор мембраны, мы имеем дополнительный фактор безопасности.
Источник
