задача 3.4.1. Труба, по которой течет вода
Тип работы: Задача
Предмет: Гидравлика
Статус: Выполнен
Год работы: 2020
Страниц: 1
Оригинальность: 86% (antiplagiat.ru)
Формат: docx ( Microsoft Word )
Цена: 148 руб.
Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
Благодаря этой странице вы научитесь сами решать такие задачи:
Другие похожие задачи:
Описание работы:
задача 3.4.1. Труба, по которой течет вода, имеет переменное сечение. Определить скорость во втором сечении, если скорость в первом сечении v1=0,05 м/с; d1=0,2 м; d2=0,1м





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
В какую сторону течёт вода?
Пятничная статья про столкновение задачи из собеседования с реальным миром.
Есть довольна известная задача — перед вами находится металлическая труба с текущей внутри водой. Как определить, в какую сторону она течёт? Её всё ещё могут задать вам на собеседованиях.
По многим задачам с неточной формулировкой уже проходились, давайте разберёмся, что же не так с этой трубой.
Ожидаемое решение — нагреть трубу и посмотреть, в какую сторону будет распространяться тепло. Но тут есть много дополнительных нюансов. Как правило подразумевается, что греть будут газовой горелкой. Встречалось даже ограничение, что у вас может быть любой предмет ценой до ста рублей, что делает задачу практически нерешаемой таким способом, но об этом позже.
Во-первых, надо быть уверенным, что температура воды достаточно низка, чтобы её можно было трогать. Ну, точнее, чтобы можно было понять разницу между «очень горячо» и «очень-очень горячо». Точно сказать сложно, но вряд ли это выше 50 градусов Цельсия.
Во-вторых, надо быть уверенным, что вода течёт со скоростью значительно большей скорости распространения тепла в воде. Например, при скорости потока 1мм/с вы вряд ли поймёте, куда вода движется и движется ли вообще.
В-третьих, надо быть уверенным, что вода не течёт со слишком большой скоростью. Иначе она просто не успеет достаточно прогреться.
Температурная чувствительность человека к разницам температур составляет примерно один градус. Исходя из теплоёмкости воды
4,2 кДж/кг получим, что на грамм протекающей воды мы должны передать в районе 4,2 Джоуля чтобы иметь возможность ощутить разницу температур.
Предположим, что подогревая трубу какой-то горелкой мы передаём трубе примерно половину теплоты сгораемого топлива. Это достаточно щедрое предположение, например хорошие газовые котлы имеют КПД в районе 95%.
Скорость потока в обычном холодном водоснабжении составляет примерно 1м/с. Для обычной трубы 1/2″, скажем в ванной, это даст расход примерно 200 г/с. Будем опираться на эти цифры чтобы иметь представление о том, какого размера должна быть труба, чтобы при привычной скорости потока мы могли определить его направление.
Зайдём с козырей. Предположим, что для решения задачи у вас есть хорошая сварочная горелка, ацетилен и кислород. Расход горелки примерно килограмм ацетилена в час, теплота сгорания примерно 50МДж/кг. Соответственно, в секунду получим примерно 13888 Дж, с учётом низкого КПД трубе передастся примерно 7000 из них. В принципе, можно прогреть на градус трубу с проходом 1.7 кг воды в секунду.
Ну… Решение вроде работает. Но давайте признаем, что большинство программистов никогда не держали в руках сварочную аппаратуру. И глядя на архитектуру некоторых приложений — это к лучшему. Пусть в качестве нагревательного прибора используется обычная газовая горелка со сменным баллоном, вроде той что используется для розжига кальянного угля. Расход газа составляет примерно 100 г/час. Для простоты расчёта возьмём теплоту сгорания пропана такой же, то есть 50МДж. В секунду мы сможем получить 700 Дж. Этого хватит для нагрева 170 грамм воды.
Выглядит уже не так перспективно. Если на дальний конец этой таинственной трубы надет шланг и моя бабушка поливает из него помидоры, то есть поток жидкости по трубе практически не ограничен, то понять направления потока мы уже не сможем. Бабуле придётся слегка зажимать шланг пальцем чтобы задача стала решаемой.
Вообще в условии подразумевалось, что смышлёный соискатель возьмёт зажигалку и нагреет трубу. Я нигде не смог найти нормы расхода газа для зажигалок. Вероятно, проводить подобные изменения никому в голову не пришло.
Возьмём данные по газовым паяльникам. Определённо, это более мощный прибор чем зажигалка, но примем эти цифры для расчёта. Газовый паяльник потребляет примерно 20 мл/час, то есть примерно 10 г/час. Значит с его помощью мы сможем нагревать на один градус примерно 17 грамм воды в секунду.
17 г/с это очень немного. Для такого расхода к трубе должен быть подключен весьма скромный потребитель, например автомат для газировки. Причём это не тот автомат как в торговом центре — пять секунд и поллитровый стакан готов. Это автомат, который наливает стакан очень медленно, с приличествующей случаю торжественностью.
Суммируя всё вышесказанное, задачу нужно было бы поставить следующим образом:
Вы находитесь в бесконечном поле. Перед вами металлическая труба толщиной не более стандартной водопроводнной. В ней течёт вода, температуры не выше 50 градусов Цельсия, со скоростью не более 1 м/с и не менее 1мм/с. Начала и конца этой трубы вы достигнуть не сможете. Какой предмет вам потребуется для определения направления движения жидкости?
Звучит довольно глупо. И это мы ещё опустили совсем уж дурацкие уточнения вроде того, что труба не сделана из галлия, температура вокруг не -190, атмосфера не состоит из гремучего газа или вас не реинкарнировало в бурундука.
Для решения задачи в хоть сколько-нибудь приближенных к реальным условиях вам требуется весьма серьёзное оборудование. С которым работать вы, кстати, скорее всего не умеете.
Как и во всех логических задачах, условности тут просто неисчислимы. Даже если взять задачу с волком козой и капустой — как такое вообще возможно? Вы голый, стоите на берегу реки, перед вами всё это добро и вам надо переправиться? Ах да, берега реки сделаны из адамантия, чтобы вы капусту закопать не догадались. В такой ситуации любой нормальный человек в первую очередь задумается, не позвать ли санитара.
Мы уже прикинули выше, для того, что нормальный человек представляет себе при фразе «труба с водой», тепловое решение практически неприменимо. По крайней мере если у вас нет случайно с собой горелки и двух баллонов.
Тем не менее, можно придумать несколько других решений. Тоже, не без ограничений, но более широко применимых.
Тепловой, но «обратный» вариант — обдуть трубу углекислотой из огнетушителя и посмотреть, как будет стаивать иней.
Можно положить на трубу камертон и слушать звук левее и правее. В направлении движения жидкости звук разнесётся дальше. Тут, впрочем, нужны достаточно большие скорости. Для совсем уж больших скоростей можно будет даже услышать эффект Доплера.
Особо мощные кандидаты могут просто пнуть трубу и посмотреть, в каком направлении волна быстрее затухнет.
При помощи зажима с регулировкой усилия можно сжать трубу, чтобы уменьшить проход, и затем замерить усилие необходимое для её сжатия с обеих сторон от сужения.
В общем решения есть. Но весьма причудливые для столь простой задачи. И все они сложнее очевидного — дойти до конца трубы. В реальном мире бесконечные трубы не встречаются. Более того, там где это важно, направление движение жидкости указывается при монтаже. И даже есть клапаны, препятствующие обратному движению.
К сожалению, такие задачи ничего о кандидате не скажут. Ну кроме того, что он любит на досуге решать головоломки.
Источник
Поиск, обзор и навигация
Магазин работ
ПиАХТ
Чертежи
Решение задач часть 1 Гидравлические испытания
1.2.1. Сосуд заполнен водой, занимающей объем W1= 2 м3. На сколько уменьшится и чему будет равен этот объем при увеличении давления на величину на величину 200 бар при температуре 20 С? Модуль объемной упругости для воды при данной температуре Ео = 2110 МПа.
1.2.2. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина 20 С. Модуль объемной упругости бензина принять равным Ео =1300 МПа, коэффициент температурного расширения bt=8*10-4 1/град
1.2.3 Плотность масла АМГ-10 при температуре 20 С составляет 850 кг/м3. Определить плотность масла при повышении температуры до 60 С и увеличении давления с атмосферного (р1=0,1 МПа) до р2=8,7 МПа. Модуль объемной упругости масла Ео =1305 МПа, температурный коэффициент ?t = 0,0008 1/град
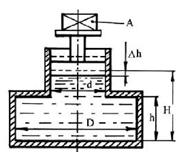
1.2.4. Определить объемный модуль упругости жидкости, если под действием груза А массой 250 кг поршень прошел расстояние ?h = 5 мм. Начальная высота положения поршня (без груза) H = 1,5 м; диаметр поршня d = 80 мм и резервуара D = 300 мм; высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким
1.7.1. При гидравлическом испытании трубопровода диаметром d = 200 мм и длиной L = 250 м давление в трубе было повышено до 3 МПа. Через час давление снизилось до 2 МПа. Сколько воды вытекло через неплотности, если модуль объёмной упругости Е0 = 2060 МПа?
Скачать решение задачи 1.7.1 (Решебник 2) (цена 60р)
1.7.2. Трубопровод диаметром d = 500 мм и длиной L = 1 км наполнен водой при давлении 0,4 МПа и температуре воды 5 С. Определить, пренебрегая деформациями и расширением стенок трубы, давление в трубопроводе при нагревании воды в нём до 15 С, если модуль объёмной упругости Е0 = 2060 МПа, а коэффициент температурного расширения t = 0,15•10-3 1/ С.
Скачать решение задачи 1.7.2 (Решебник 2) (цена 60р)
1.7.7. Компрессор, имеющий производительность Tк = 1,8 норм. м3/мин, сжимает воздух до 8 бар. Температура атмосферного воздуха на входе в компрессор составляет tв = 20 С, относительная влажность равна ф = 70 %. В ресивере сжатый воздух охлаждается до 25 С. Сколько воды выпадает в ресивере в течение часа?
Скачать решение задачи 1.7.7 (Решебник 2) (цена 60р)
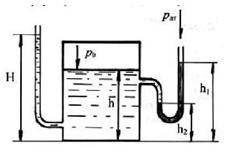
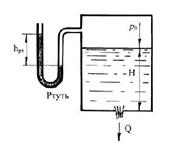
2.5.2. Определить давление Рo воздуха в напорном баке по показанию ртутного манометра. Какой высоты Н должен быть пьезометр для измерения того же давления Рo? Высоты h=2,6 м; h1=1,8 м; h2=0,6 м. Плотность ртути ppm= 13600 кг/м3, воды p= 1000 кг/м3
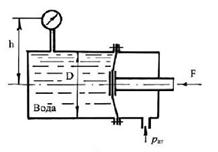
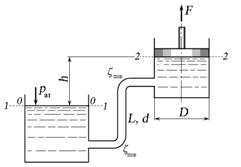
2.5.3. Определить силу F, действующую на шток гибкой диафрагмы, если ее диаметр D = 200 мм, показания вакуумметра рвак = 0,05 МПа, высота h = 1 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если ha = 740 мм. рт. ст.
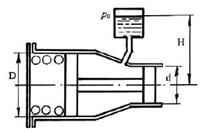
2.5.4. Система из двух поршней, соединенных штоком, находится в равновесии. Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке — масло с плотностью p = 870 кг/м3. Диаметры D =80 мм; d = 30 мм; высота Н = 1000 мм; избыточное давление р0 = 10 кПа.
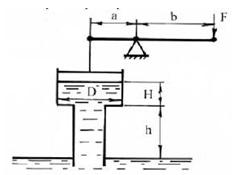
2.5.5. Определить силу Р, необходимую для удержания в равновесии поршня, если труба под поршнем заполнена водой, а размеры трубы: В =100 мм; Н = 0,5 м; h = 4м. Длины рычага: а = 0,2 м и b =1 м. Собственным весом поршня пренебречь.
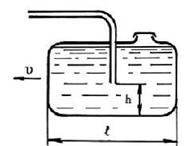
2.5.6 Топливный бак автомобиля длиной L=0,6м, шириной b = 0,5 м и высотой Н = 0,2 м движется с ускорением а = 3,27 м/с2. Определить минимальное количество топлива в баке, обеспечивающее его подачу без подсоса воздуха. Считать, что бензопровод установлен в центре горизонтальной проекции бака, его диаметр мал по сравнению с длиной бака, высота h = 10 мм.
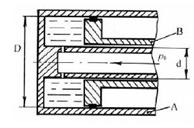
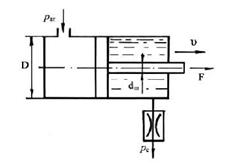
2.5.7 На рис показан элемент одной из возможных схем гидроусилителя сцепления автомобиля (трактора). Масло под давлением р0 = 0,5 МПа подводится внутри вала и затем через отверстие – в полость между двумя совместно вращающимися цилиндром А и поршнем Б, который может скользить вдоль вала. Давление масла, увеличенное благодаря действию центробежных сил, заставляет поршень перемещаться вправо и обеспечивает этим силу нажатия, необходимую для включения сцепления. Определить силу давления масла на поршень Б, если его диаметр D =120 мм; диаметр вала d = 20 мм; частота вращения n = 6 000 об/мин; плотность жидкости p = 920 кг/м3.
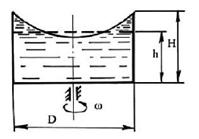
2.5.8 В сосуд высотой Н = 0,3 м залита жидкость до уровня h = 0,2м. Определить, до какой угловой скорости можно раскрутить сосуд, с тем, чтобы жидкость не выплеснулась из него, если диаметр сосуда D = 100 мм.
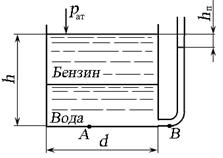
2.7.1. В цилиндрический бак диаметром d = 2 м до уровня h = 1,5 м налиты вода и бензин. Уровень воды в пьезометре, открытом в атмосферу, ниже уровня бензина на hп = 300 мм. Определить объём находящегося в баке бензина, если плотность бензина ?б = 700 кг/м3, плотность воды pв = 1000 кг/м3.
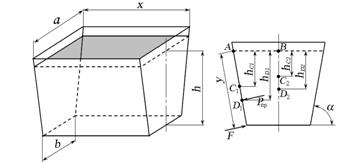
2.7.9. Резервуар заполнен жидкостью плотностью p = 870 кг/м3, высота столба жидкости h = 0,65 м. Основания трапеции боковой стенки а = 0,6 м, b = 0,35 м, длина х = 1,2 м. Определить усилие, действующее на каждый болт крепления боковых стенок и дна резервуара на глубине h, если количество болтов по длине х равно nх = 8 шт., по длине b равно nb = 3 шт. Определить диаметр болтов, если допустимое напряжение на разрыв стального болта = 7000 Н/см2.
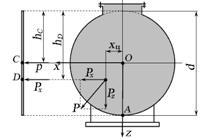
2.7.10 Горизонтальная металлическая цистерна круглого сечения диаметром d = 2 м и длиной L = 10 м полностью заполнена минеральным маслом (удельный вес масла 9•103 Н/м3). Давление на поверхности масла равно атмосферному. Определить силу давления масла на внутреннюю криволинейную поверхность цистерны. Определить координаты центра тяжести тела давления.
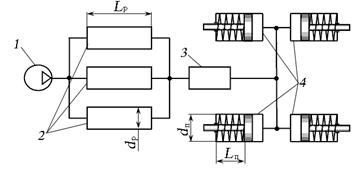
2.7.11 Определить диаметр dр резервуаров — накопителей (ресиверов) 2 автоматической системы тормозов автомобиля, при котором будет обеспечиваться шесть торможений (n = 6) за счёт сжатого воздуха без включения компрессора 1. Последний включается и начинает нагнетать воздух в систему при избыточном давлении р2 = 0,4 МПа и выключается при р1 = 0,6 МПа. Кран управления 3 после каждого торможения выпускает воздух из тормозных цилиндров 4 в атмосферу. Принять: диаметр поршня тормозных камер dп = 180 мм, ходы поршней Lп = 0,06 м, длины резервуаров Lр = 0,8 м, атмосферное давление составляет 749,5 мм. рт. ст. Процесс расширения воздуха считать изотермическим. Объёмом трубопроводов пренебречь. Определить, сколько полных торможений без включения компрессора могут обеспечить эти резервуары, если автомобиль въехал на горный перевал (где атмосферное давление составляет 400 мм. рт. ст.) без использования тормозной системы.
3.4.1. Труба, по которой течет вода, имеет переменное сечение. Определить скорость во втором сечении, если скорость в первом сечении v1=0,05 м/с; d1=0,2 м; d2=0,1м
3.4.2. По трубопроводу диаметром d = 150 мм перекачивается нефть плотностью ? = 800 кг/м3 в количестве 1200 т. в сутки. Определить секундный объемный расход нефти Q и среднюю скорость ее течения ?
3.4.3 По полностью затопленному трубопроводу перекачивается жидкость со скоростью 0,2 м/с. Определить расход жидкости Q, если гидравлический радиус R = 0,015 м.
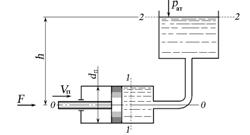
3.9.1. Поршень диаметром dп = 8 см перемещается со скоростью Vп под действием силы F = 0,4 кН. Жидкость плотностью p = 870 кг/м3 под действием поршня из правой части гидроцилиндра перемещается в бак, открытый в атмосферу. Определить скорость перемещения поршня Vп, если высота h = 9,4 м.
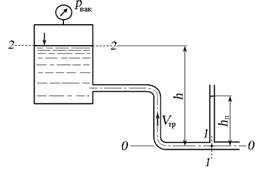
3.9.2. Определить вакуумметрическое давление в баке рвак, при котором скорость течения потока жидкости в трубопроводе составит Vтр = 1,2 м/с. Высота h = 3,2 м, плотность жидкости ? = 870 кг/м3. Высота уровня жидкости в пъезометре составляет hп = 0,64 м.
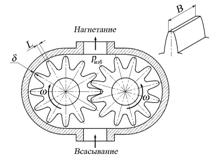
3.9.3. Определить утечки через радиальные зазоры в шестерённом насосе вследствие разности давлений в нагнетательной и всасывающей полости. Высота каждого зазора ? = 0,09 мм, длина зазора L = 2 мм, ширина В = 30 мм, перепад давлений р = 1,32 МПа, наружный диаметр шестерни D = 62 мм, частота вращения n = 1450 об/мин, вязкость масла m = 0,012 Па•с.
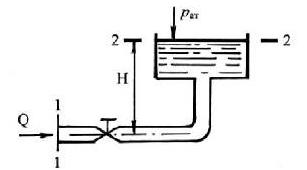
4.3.1. Вода под напором движется в бак, расположенный на высоте h от оси трубопровода. Определить высоту h до уровня воды в баке, открытом в атмосферу, если вязкость воды v = 0,01 Ст, диаметр трубопровода d = 10 мм, длина L = 20 м, пъезометрический напор в сечении 1 — 1 принять Hп = 20 м. Расход воды в трубопроводе составляет Q = 0,072 л/с. Коэффициенты сопротивления крана Cкр = 4, поворота Cпов = 1. Трубу считать гидравлически гладкой.
4.3.2. Поршень диаметром D = 200 мм движется равномерно вверх, всасывая воду. Диаметр трубопровода d = 50 мм, его длина L = 12 м, коэффициент гидравлического трения л = 0,03, коэффициент местного сопротивления (поворота) Спов = 0,5. При высоте h = 2 м сила, необходимая для перемещения поршня вверх, равна F = 2,35 кН. Определить скорость перемещения поршня. Найти, до какой высоты hmax можно поднять поршень без возникновения кавитации, если давление насыщенного пара рнп = 4,25 кПа, плотность воды ? = 1000 кг/м3. Атмосферное давление принять рат = 98,7 кПа. Весом поршня и трением пренебречь.
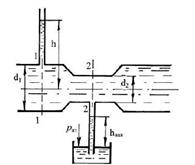
4.5.2. Определить, на какую высоту поднимется вода в трубке, один конец которой присоединен к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды в трубе Q = 0,025 м3/с; избыточное давление р1 = 49 кПа; диаметры d1 = 100 мм и d2 = 50 мм. Потерями напора пренебречь.
5.6.1. Определить число Рейнольдса и режим движения воды в водопроводнойтрубе диаметром d = 300 мм, если расход Q = 0,136 м3/с. Коэффициент кинематической вязкости для воды (при t = 10 °С ) V = 1,306-10 -6 м 2 /с.
5.6.2. По трубопроводу диаметром d = 100 мм транспортируется нефть. Определить критическую скорость, соответствующую переходу ламинарного движения жидкости в турбулентное. Коэффициент кинематической вязкости принять равным V = 8,1*10 -6 м 2 /с.
5.6.3 Как изменяется число Рейнольдса при переходе трубопровода от меньшего диаметра к большему при сохранении постоянства расхода (Q = const)?
6.4.1. Вентиляционная труба d = 0,1 м имеет длину l = 100 м. Определить потери давления, если расход воздуха, подаваемый по трубе, равен Q = 0,078 м3/с. Давление на выходе равно атмосферному (Pат = 0,1 МПа). Местные сопротивления по пути движения воздуха отсутствуют. Кинематическая вязкость воздуха при t = 20 С составляет 15,7•10-6 м2/с. Средняя шероховатость выступов 0,2 мм, плотность воздуха p = 1,18 кг/м3.
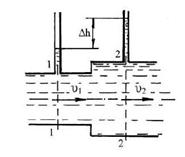
6.4.2. При внезапном расширении трубы от d = 50 мм до D = 150 мм происходит увеличение давления, которому соответствует разность показаний пъезометров ?h = 80 мм. Определить скорости v1 и v2 и расход жидкости. Учесть потери на внезапное расширение.
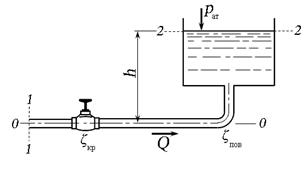
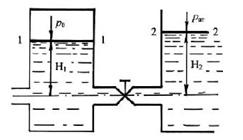
6.4.3 Вода перетекает из напорного бака, где избыточное давление воздуха р1 = 0,3 МПа, в открытый резервуар по короткой трубе диаметром d =50 мм, на которой установлен кран. Чему должен быть равен коэффициент сопротивления крана для того, чтобы расход воды составлял Q = 8,7 л/с. Высоты уровней Н1 = 1м, Н2 = 3 м. Учесть потери напора на входе в трубу (0,5) и на выходе из трубы (внезапное расширение).
7.3.1. Определить расход и скорость вытекания воды из малого круглого отверстия диаметром d = 3 см в боковой стенке резервуара больших размеров. Напор над центром отверстия Н = 1 м, кинематическая вязкость воды при t = 20 °С составляет v = 10 -6 м 2 /с.
7.3.2. Определить расход жидкости (p = 800 кг/м3), вытекающей из бака через отверстие площадью S = 1 см2. Показание ртутного манометра h = 268 мм, высота Н = 2 м, коэффициент расхода отверстия 0,60.
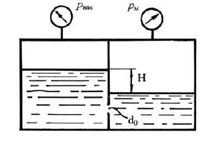
7.3.3. Определить направление истечения жидкости с плотностью p = 1000 кг/м3 через отверстие d0 = 5 мм и расход, если разность уровней Н = 2 м, показание вакуумметра соответствует 147 мм. рт. ст., показание манометра hм=0,25 МПа, коэффициент расхода 0,62.
7.3.4. Определить диаметр отверстия дросселя, установленного на сливе из гидроцилиндра, при условии движения штока цилиндра под действием внешней нагрузки F= 60 кН со скоростью v = 200 мм/с. Диаметры: штока dш = 40 мм, цилиндра D = 80 мм, коэффициент расхода дросселя 0,65, плотность жидкости p = 850 кг/м3 , давление на сливе рс = 0,3 МПа.
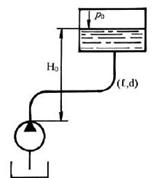
8.5.1. На рисунке показан всасывающий трубопровод гидросистемы. Длина трубопровода ? = 1м, диаметр d = 20 мм, расход жидкости Q = 0,314 л/с, абсолютное давление воздуха в бачке р0 = 100 кПа, высота Н = 1м, плотность жидкости p = 900 кг/м3. Определить абсолютное давление перед входом в насос при температуре рабочей жидкости t = 25°С (v = 0,2•10-4 м2/с). Как изменится искомое давление в зимнее время, когда при этом же расходе температура жидкости упадет до -35°С (v = 10•10-4 м2/с).
8.5.2 По трубопроводу диаметром d = 10 мм и длиной l = 10 м подается жидкость с вязкостью ? = 0,0001 м2/с под действием перепада давления Pр = 4 МПа; плотность p = 1000 кг/м3. Определить режим течения жидкости в трубопроводе.
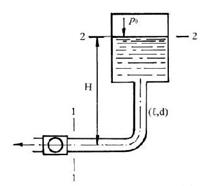
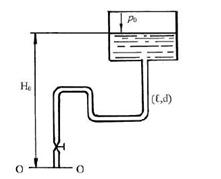
8.5.3. Определить потребный напор, который необходимо создать в сечении 0-0 для подачи в бак воды с вязкостью 0,008 м2/с, если длина трубопровода l = 80 м; его диаметр d = 50 мм; расход жидкости Q = 15 л/с; высота Н0 = 30 м; давление в баке р2 = 0,2 МПа; коэффициент сопротивления крана 5; колена 0,8; шероховатость стенок трубы 0,04 мм.
8.5.4. Определить расход в трубе для подачи воды (вязкость ? = 0,01 Ст) на высоту Н = 16,5 м, если диаметр трубы d = 10 мм, ее длина l = 20 м, располагаемый напор в сечении трубы перед краном Нрасп = 20 м, коэффициент сопротивления крана 4, колена 1. Трубу считать гидравлически гладкой.
8.5.5. При каком диаметре трубопровода подача насоса составит Q = 1 л/с, если на выходе из него располагаемый напор Нрасп = 9,6 м; длина трубопровода l = 10 м; эквивалентная шероховатость 0,05 мм; давление в баке р0 = 30 кПа; высота Н0 = 4 м; вязкость жидкости 0,015 Ст (0,0000015 м2/с) ; плотность 1000 кг/м3? Местными гидравлическими сопротивлениями в трубопроводе пренебречь. Учесть потери при входе в бак.
8.5.6. Трубопровод с расходом жидкости Q = 0,32 л/с в точке М разветвляется на два трубопровода: первый размерами l1 = 1,0 м; d1 = 10 мм; второй размерами l2 = 2,0 м; d2 = 8 мм. В точке N эти трубопроводы смыкаются. Во втором трубопроводе установлен фильтр Ф, сопротивление которого эквивалентно сопротивлению в трубе длиной dэ = 200d2. Определить расход и потерю давления в каждом трубопроводе при р = 900 кг/м3; v = 1Ст.
Источник