Коэффициент объемного сжатия
Гидравлика. Гидростатика
Основное назначение сборника – дать студентам материал, который позволит выработать навыки применения теоретических сведений к решению конкретных задач технического характера и тем самым освоить практику гидравлических расчётов.
Данный курс является основной теоретической дисциплиной для специальностей 2903, 2908, 2909, 1507, 1709.
Данный сборник содержит задачи по гидростатике и включает разделы: “Физические свойства жидкости”, “Гидростатическое давление” и “Относительный покой жидкости”.
Каждый раздел сборника содержит достаточно полные сведения из теории, касающейся материала данного раздела, методические указания и примеры решения некоторых типовых задач.
В четырёх приложениях даются материалы справочного характера, которые необходимы для решения задач.
Наличие в сборнике обширного и разнообразного материала позволяет составить индивидуальное задание для каждого студента.
После ознакомления с соответствующим теоретическим материалом и методическими указаниями по решению типовых задач, следует переходить к самостоятельному выполнению полученного задания.
Каждое задание состоит из нескольких задач, номера и варианты которых выдаются преподавателем. Задание выполняется на листах формата А4, необходимые чертежи выполняются с соблюдением выбранного масштаба.
ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ
Сведения из теории
Жидкостью называется физическое тело, обладающее двумя отличительными особенностями: незначительным изменением своего объема под действием больших внешних сил и текучестью, легкоподвижностью, т.е. изменением своей формы под действием даже незначительных внешних сил. Одной из основных механических характеристик жидкости является плотность.
Плотность.
Плотностью r (кг/м 3 ) называется масса единицы объема жидкости:
, (1.1)
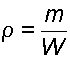
где m – масса жидкого тела, кг; W – объем, м 3 .
Плотность жидкостей уменьшается с увеличением температуры. Исключение представляет вода в диапазоне температур от 0 до 4 0 С, когда ее плотность увеличивается, достигая наибольшего значения при температуре 4 0 С r = 1000 кг/м 3 .
Удельный вес
Удельным весом g (Н/м 3 ) жидкости называется вес единицы объема этой жидкости:
, (1.2)
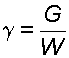
где G – вес жидкого тела, Н; W – объем, м 3 .
Для воды при температуре 4 0 С g = 9810 Н/м 3 .
Между плотностью и удельным весом существует связь:
, (1.3)
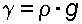
где g – ускорение свободного падения, равное 9,81 м/с 2 .
Сопротивление жидкостей изменению своего объема под действием давления и температуры характеризуется коэффициентами объемного сжатия и температурного расширения.
Коэффициент объемного сжатия
Коэффициент объемного сжатия b w (Па -1 ) – это относительное изменение объема жидкости при изменении давления на единицу:
, (1.4)
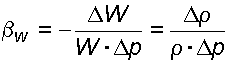
где D W – изменение объема W; D r – изменение плотности r , соответствующие изменению давления на величину D p.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкостей Eж (Па)
. (1.5)
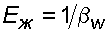
Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давления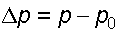 
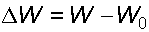
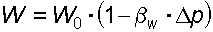
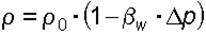
, а изменение объема 
то:
; (1.6)
. (1.7)
1.1.4. Коэффициент температурного расширения
- Коэффициент температурного расширения b t ( 0 С) -1 , выражает относительное изменение объема жидкости при изменении температуры на один градус:
, (1.8)
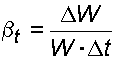
где D W – изменение объема W, соответствующее изменению температуры на величину D t.
Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей b t с увеличением давления уменьшается. Если принять, что приращение температуры D t = t – t0, а изменение объема
; (1.9)
. (1.10)
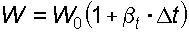
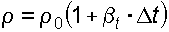
Вязкостью называется свойство жидкости оказывать сопротивление перемещению одной части жидкости относительно другой. Вязкость проявляется только при движении жидкости и сказывается на распределении скоростей по живому сечению потока (рис. 1.1).
Согласно гипотезе Ньютона сила внутреннего трения F в жидкостях пропорциональна градиенту изменения скорости 
, площади соприкосновенияслоев S, зависит от рода жидкости и очень незначительно зависит от давления.
, (1.11)
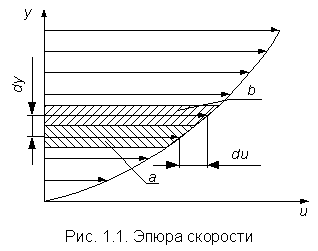
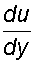
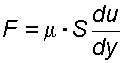
где S – площадь соприкасающихся слоев, м 2 ; du – скорость смещения слоя «b» относительно слоя «a«, м/с; dy – расстояние, на котором скорость движения слоев изменилась на du, м;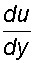 
– градиент скорости, изменение скорости по нормали к направлению движения (с -1 ); m – коэффициент динамической вязкости (Па · с).
Если силу трения F отнести к единице площади соприкасающихся слоев, то получим величину касательного напряжения t , и тогда (1.11) примет вид:
. (1.12)
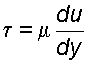
Из (1.12) следует, что коэффициент динамической вязкости может быть определен как:
. (1.13)
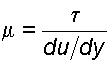
Из (1.13) нетрудно установить физический смысл коэффициента динамической вязкости. При градиенте скорости 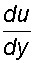= 1; m = t и выражает силу внутреннего трения, приходящуюся на единицу площади поверхности соприкасающихся слоев жидкости.
В практике, для характеристики вязкости жидкости, чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости n (м 2 /с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:
. (1.14)
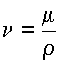
Вязкость жидкости зависит от рода жидкости, от температуры и от давления.
Зависимость вязкости минеральных масел, применяемых в гидросистемах, от давления p при возрастании его до 50 МПа, можно определять с помощью приближенной эмпирической формулы:
, (1.15)
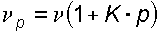
где n p и n – кинематическая вязкость соответственно при давлении p и 0,1 МПа; K – опытный коэффициент, зависящий от марки масла: для легких масел (n 50 -6 м 2 /с) К = 0,02, для тяжелых масел (n 50 > 15 10 -6 м 2 /с) К = 0,03. При незначительных давлениях изменением вязкости пренебрегают. С повышением температуры вязкость жидкости уменьшается. Зависимость коэффициента кинематической вязкости от температуры определяется по эмпирической формуле:
. (1.16)
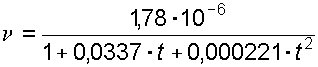
Для смазочных масел, применяемых в машинах и гидросистемах, рекомендуется следующая зависимость:
, (1.17)
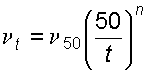
где n t – кинематическая вязкость при температуре t; n 50 – кинематическая вязкость при температуре 50 0 С; n – показатель степени, зависящий от n 50, определяемый по формуле:
. (1.18)
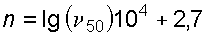
Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера ( 0 Е). Градус Энглера ( 0 Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости n применяется формула Убеллоде:
. (1.19)
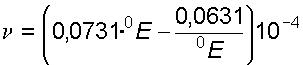
Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости в этом случае определяют по формуле:
, (1.20)
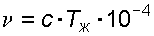
где с – постоянная прибора; Tж – время истечения жидкости, с.
Источник
Физические свойства жидкости
К основным физическим свойствам жидкости, которые рассматриваются в гидродинамике, относятся плотность, удельный вес, удельный объем, температурное расширение, сжимаемость и вязкость.
Плотность — это отношение массы вещества к его объему:
На плотность жидкости влияют температура и давление. Значения плотности некоторых жидкостей приведены ниже:
- Жидкость: р, кг/м3
- Вода: 1000
- Антифриз: 1070
- Бензин: 750
- Керосин: 800
- Дизельное топливо: 860
- Масло МГ- 15-Б: 850
- МГ-22-А: 880
- ТМ-5-18: 900
- Нефть: 900
- Ацетон: 700
- Спирт: 800
- Глицерин: 1260
Удельный вес — это отношение веса жидкости к занимаемому объему:
Удельный объем жидкости — объем единицы массы этой жидкости:
Температурное расширение — свойство жидкости изменять свой объем при изменении температуры. С ростом температуры объем жидкости увеличивается и наоборот. Различные жидкости при увеличении температуры на одну и ту же величину увеличиваются в объеме по разному. Поэтому свойство жидкости увеличиваться в объеме с увеличением температуры характеризуется коэффициентом температурного расширения Bт, который показывает изменение единицы объема данной жидкости при изменении ее температуры на 1 К.
- Жидкость — Bт (10^-4, К^-1)
- Вода: 2
- Антифриз: 5
- Нефть: 8
- Ртуть: 1,8
Увеличение объема при нагревании рассчитывается по уравнению:
дельта V= Bт*V0*дельта Т
где V0 начальный объем жидкости; дельта Т— изменение температуры.
В расчетах ДВС коэффициент температурного расширения считают постоянным, хотя на самом деле он зависит от условий нагревания или охлаждения, давления и начальной температуры.
Сжимаемость — свойство жидкости изменять объем при изменении давления.
дельта V = Bр*V0*дельта р,
где дельта V— изменение объема; дельта р — изменение давления; Вр — коэффициент объемного сжатия.
Коэффициент объемного сжатия показывает изменение единицы объема жидкости при изменении давления на 1 Па. Он зависит от условий сжатия, температуры и начального давления. При расчетах эта зависимость не учитывается.
Коэффициент объемного сжатия для воды равен 5 * 10^-4 1/Па, для нефтепродуктов — 7*10^-4 1/Па, для ртути — 0,3*10^-4 1/Па.
Ввиду незначительных величин жидкости считаются несжимаемыми.
Вязкость — свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой.
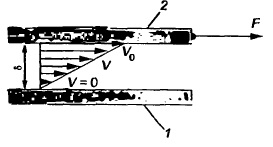
Рис. Схема изменения скорости жидкости, заключенной между неподвижной (1) и подвижной (2) пластинами
Если плоскость 2, находящаяся на расстоянии б от плоскости 1, под действием силы F перемещается со скоростью V0, то слои жидкости, находящиеся между плоскостями, перемещаются с разными скоростями. При этом максимальная скорость V0 в точках контакта с плоскостью 2, минимальная (вплоть до нуля) в точках контакта с плоскостью 1.
Если слои жидкости при движении не перемешиваются, то скорость в потоке изменяется по линейному закону, и отношение V0/б представляет собой градиент скорости.
При скольжении слоев жидкости между ними возникают силы внутреннего трения, которые сопротивляются движению. На преодоление этих сил и расходуется внешняя сила F:
где n — динамический коэффициент вязкости или динамическая вязкость; S — площадь трения (жидкости о пластину).
Динамическая вязкость учитывает свойства жидкости, от которых зависит ее внутреннее трение. В технике и в частности в гидравлике часто используется кинематическая вязкость v, которая равна отношению динамической вязкости жидкости к ее плотности:
Для упрощения решения гидродинамических задач считают, что рассматриваемые жидкости не обладают температурным расширением, сжимаемостью и вязкостью. Такие жидкости в отличие от реальных называются идеальными.
Источник
