- Energy education
- сайт для тех, кто хочет изучать энергетику
- Механика жидкости и газа
- Примеры выполнения заданий
- Примеры решения задач по теме «Основные законы движения жидкости»
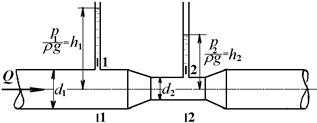
- Примеры решения задач. Пример № 7.1. Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0,2 м, имеющем сужение диаметром d2 = 0,12 м (рис
Energy
education
сайт для тех, кто хочет изучать энергетику
Механика жидкости и газа
Примеры выполнения заданий
В качестве примеров выполнения заданий рассмотрен вариант их решения.
Примеры решения задач по теме «Основные законы движения жидкости»
1. Определить число Рейнольдса для воздушного канала размерами $300х470$ мм, если кинематическая вязкость воздуха составляет $14.16·10^<-6>$ м 2 /с, а расход воздуха равен $40$ м 3 /ч.
2. Вода движется в лотке со скоростью $0.1$ м/c. Глубина наполнения лотка $h=30$ см, ширина по верху $В=50$ см, ширина по низу $b=20$ см. Определить режим движения жидкости, если температура воды составляет $10$ °С.
3. Вода движется в треугольном лотке с расходом $Q=0.5$ л/c. Ширина потока $b=0.8$ м, глубина наполнения $h=0.3$ м. Определить, при какой температуре будет происходить смена режимов движения жидкости.
4. Вода движется в безнапорном трубопроводе с температурой $t=30$ ºC. Трубопровод заполнен на $70$% сечения. Диаметр трубопровода $d=50$ мм. Определить, при какой скорости будет происходить смена режимов движения жидкости.
5. Определить скорость движения воды в трубе, если разница уровней составляет $5$ см.
6. На рисунке представлен водомер Вентури (участок трубы с плавным сужением потока), предназначенный для измерения расхода протекающей по трубопроводу жидкости. Определить расход воды, если разность уровней в трубках дифференциального ртутного манометра $h=20$ см, диаметр трубы $d_1=250$ мм, диаметр горловины (сужения) $d_2=125$ мм. Потерями напора в водомере пренебречь.
7. На водопроводной трубе диаметром $d_1=0.1$ м установлен водомер Вентури диаметром $d_2=0.05$ м. На какую высоту $h_2$ поднимется вода в пьезометрической трубке, присоединенной к суженному сечению, при пропуске расхода $Q=0.005$ м 3 /c, если уровень воды в пьезометре, присоединенном к трубе, $h_1=0.8$ м. Потери напора не учитывать.
8. Определить теоретический расход воды, проходящий через водомер Вентури, установленный под углом $α=30$° к горизонту, если разность уровней, показываемая дифференциальным ртутным манометром, равна $h=6$ мм.рт.ст. Плотность ртути равна $13600$ кг/м 3 . Больший и меньший диаметры водомера соответственно равны $d_1=150$ мм и $d_2=70$ мм, расстояние между сечениями $L=400$ мм. Температура воды составляет $25$ °С




9. Определить диаметр суженной части трубопровода $d_2$, если вода в трубке поднимается на высоту $h=3.5$ м при расходе воды в трубопроводе $Q=0.002$ м 3 /c и диаметре $d_1=0.1$ м. Абсолютное давление в сечении трубопровода диаметром $d_1$ $р_1=1.5·0^5$ Па. Потери напора не учитывать. Температура воды составляет $35$ °С.
10. По нагнетательному патрубку диаметром $d_1=200$ мм вентилятором подается воздух ($ρ=1.2$ кг/м 3 ) с расходом $Q=0.8$ м 3 /c при избыточном давлении $р_1=1.0$ кПа. К патрубку подсоединен диффузор с диаметром выходного сечения $d_2=300$ мм. Определить давление воздуха на выходе из диффузора. Изменение плотности воздуха и потери в диффузоре не учитывать.
Администратор сайта: Колосов Михаил
email:
Copyright © 2011-2021. All rights reserved.
Источник
Примеры решения задач. Пример № 7.1. Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0,2 м, имеющем сужение диаметром d2 = 0,12 м (рис



Пример № 7.1.
Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0,2 м, имеющем сужение диаметром d2 = 0,12 м (рис. 7.1). Разность показаний пьезометров Dh = 250 мм.
Dh = 250 мм = 0,25 м.
Рисунок 7.1 Определить: Q.
Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 1-1 и 2-2:
z1 + 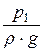
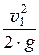
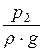
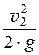
Для горизонтального трубопровода z1 = z2. Обозначим пьезометрические высоты h1 = 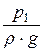
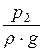
Dh = a2 × 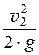
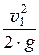
Из уравнения неразрывности v1 × w1 = v2 × w2 выразим скорость во втором сечении:
v2 = v1 × 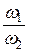
Для круглого напорного трубопровода площадь живого сечения потока w = 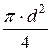
v2 = v1 × 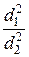
Подставляя это выражение в уравнение Бернулли имеем:
Dh = a2 × 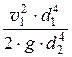
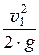
Считаем, что течение жидкости в трубопроводе турбулентное. Принимаем коэффициент Кориолиса a1 = a2 = a = 1,1.
Dh = a × 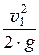
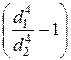
v1 = 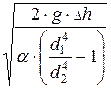
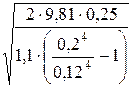
Объёмный расход равен:
Q = v1 × w1 = v1 × 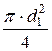
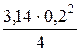
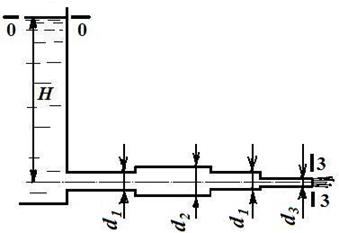
Пример № 7.2. Жидкость вытекает из резервуара большого сечения по горизонтальному трубопроводу переменного сечения. Определить расход Q в горизонтальном трубопроводе (рис. 7.2), скорость на каждом из участков vi и построить пьезометрическую линию 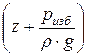
Рисунок 7.2 Решение
Составим уравнение Бернулли (энергии) без учёта потерь энергии для двух сечений: 0-0 (свободная поверхность жидкость в резервуаре, из которого истекает жидкость) и 3-3 (выходное сечение трубопровода):
z0 + 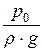
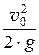
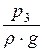
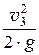
Здесь р0 – давление на свободную поверхность жидкости в открытом резервуаре равно атмосферному давлению, то есть р0 = рбар. р3 – давление в выходном сечении трубопровода. Оно равно давлению той среды, куда происходит истечение. В данном случае р3 = рбар.
Горизонтальную плоскость сравнения совместим с осью трубопровода переменного сечения. Тогда z0 = Н, а z3 = 0.
Скорость на свободной поверхности жидкости в резервуаре v0 пренебрежимо мала по сравнению со скоростью жидкости в трубопроводе переменного сечения vi. Поэтому полагаем, что v0 » 0.
Принимаем, что коэффициент Кориолиса a.3 =1,0. (На практике мы обычно имеем дело с турбулентным движением жидкости.). Уравнение Бернулли имеет вид:
Н + 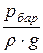
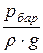
Н = 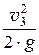
v3 = 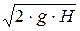
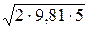
Используя уравнение неразрывности течения определяем расход жидкости в трубопроводе:
Q = v3 × w3 = v × 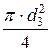
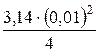
Используя это же уравнение, определяем скорости на участках диаметром d1 и d2:
Q = v1 × w1. Þ v1 = 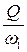
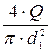
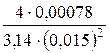
Q = v2 × w2. Þ v2 = 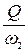
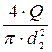
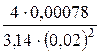
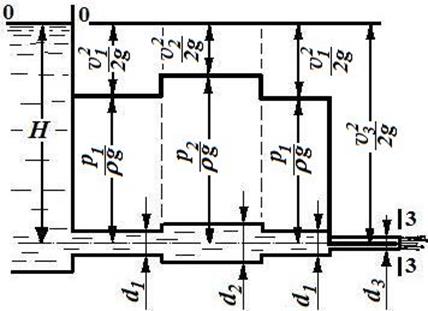
Пьезометрическую линию строят, исходя из следующих положений. Поскольку задача решается без учёта потерь энергии, то напорная линия (линия полной энергии) — 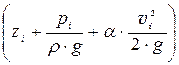
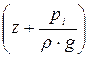
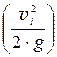
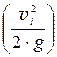
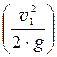
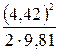
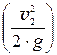
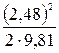
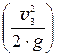
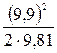
Рисунок 7.3 – Построение пьезометрической линии
Источник