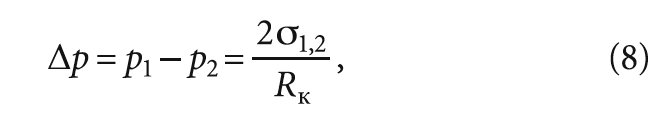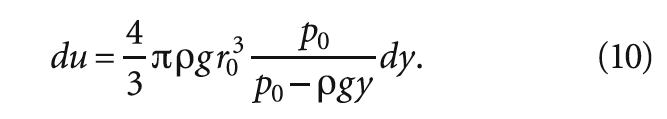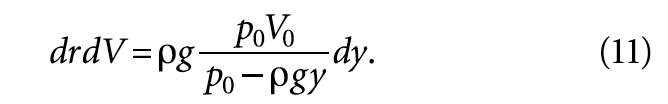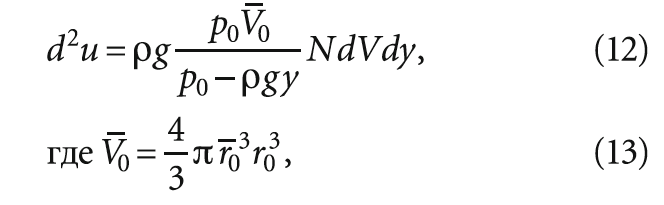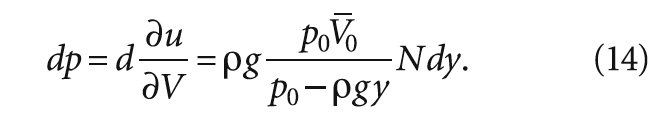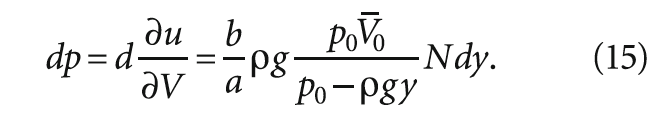Теоретические исследования движения пузырьков воздуха в потоке воды при аэрации
УДК 628.16. Научная специальность: 05.23.04.
Теоретические исследования движения пузырьков воздуха в потоке воды при аэрации
В. Б. Викулина, к.т.н., доцент; Л. В. Инешина, студентка бакалавриата, Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ)
Аэрационные сооружения, используемые в очистке воды, требуют оптимизации технологического процесса по признакам формирования и распределения воздушных масс в потоке водоочистного сооружения. В качестве транспортного потока в водоочистных сооружениях используется вода, поэтому это обстоятельство позволяет использовать законы гидродинамики потока при всплытии пузырьков воздуха в качестве дополнительного фактора. В статье приводятся физические принципы всплытия пузырьков воздуха при аэрации. Теоретически обосновывается всплывание пузырьков воздуха в статических условиях жидкости и динамических условиях потока. Получена теоретическая зависимость, которая направлена на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.
Ключевые слова: аэрация, пузырёк воздуха, вязкость динамическая, скорость потока, граница раздела фаз, распределение скоростей.
UDC 628.16. The number of scientific speciality: 05.23.04.
Theoretical studies of the motion of air bubbles in the water flow during aeration
V. B. Vikulina, PhD, Associate Professor; L. V. Inesina, undergraduate student, Moscow State University of Civil Engineering (MGSU)
Aeration facilities used in water treatment require optimization of the technological process on the basis of the formation and distribution of air masses in the flow of the water treatment plant. Water is used as a transport flow in water treatment facilities, so this circumstance allows to use the laws of flow hydrodynamics at the ascent of air bubbles as an additional factor. Physical principles of air bubbles ascent during aeration are given. Theoretically justified the rise of air bubbles in static fluid conditions and dynamic flow conditions. The obtained theoretical dependence, which is aimed at the normalization of instability of operation of the aeration structures and the determination of optimal process conditions.
Keywords: aeration, air bubble, dynamic viscosity, flow rate, phase boundary, velocity distribution.
Аэрационные сооружения, используемые в очистке воды, требуют оптимизации технологического процесса по признакам формирования и распределения воздушных масс в потоке водоочистного сооружения. В качестве транспортного потока в водоочистных сооружениях используется вода, поэтому это обстоятельство позволяет использовать законы гидродинамики потока при всплытии пузырьков воздуха в качестве дополнительного фактора. В статье приводятся физические принципы всплытия пузырьков воздуха при аэрации. Теоретически обосновывается всплывание пузырьков воздуха в статических условиях жидкости и динамических условиях потока. Получена теоретическая зависимость, которая направлена на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.
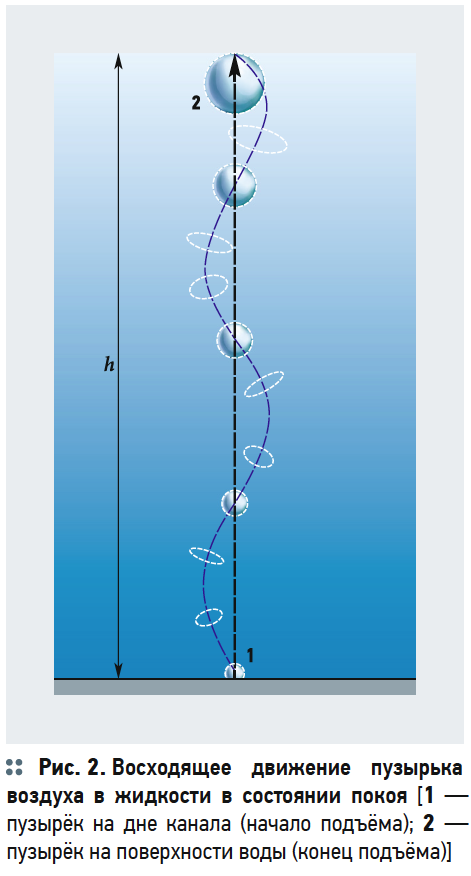
Движение потоков в сооружениях водоочистки с аэрацией (например, аэротенк, аэрофильтр, аэрируемая песколовка) создают технологическую особенность. Основным процессом, в физическом понимании аэрации, является движение пузырьков воздуха снизу вверх. Рассмотрим всплывание пузырька воздуха в жидкости, находящейся в состоянии покоя.
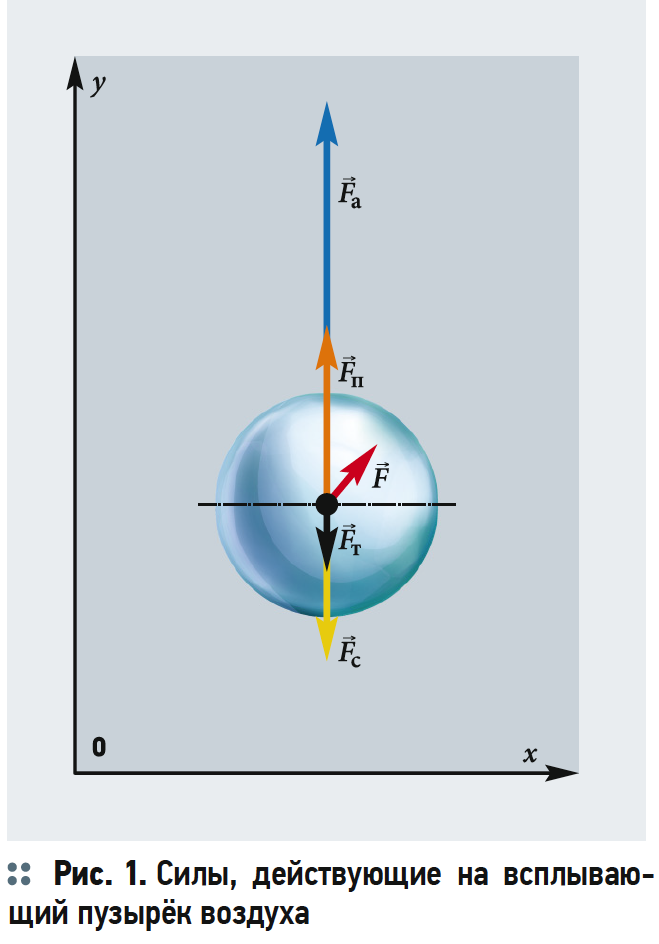
Предположим, что пузырёк воздуха в жидкости имеет форму шара [1].
На всплывающий пузырёк действуют три силы: сила тяжести Fт, архимедова сила Fа и сила сопротивления Fc (рис. 1). В проекции на вертикальную ось OY подъёмная сила Fп равна:
Силы выражаются в ньютонах (Н).
Рассмотрим действие сил при равномерном движении пузырька в воде.
Сила Архимеда (выталкивающая сила) приводит пузырёк в движение вверх, при этом диаметр пузырька увеличивается, достигая своего максимума на поверхности воды.
Сила Стокса (сила трения) при движении пузырька действует в направлении, противоположном силе Архимеда, и направлена сверху вниз.
Сила тяжести действует в условиях ускорения свободного падения и направлена сверху вниз.
Сила Стокса возникает в результате взаимодействия жидкости с пузырьком и равна силе трения, на преодоление которой затрачивается работа.
Разность энергий двух состояний пузырька до начала совершения работы и после — это работа как избыточная свободная энергия. С точки зрения гидростатики дополнительная потенциальная энергия равносильна динамическому напору.
При условии сжимаемости воздуха и при движении пузырька вверх наружное давление на стенки пузырька будет меняться с высотой, а диаметр пузырька будет увеличиваться. Расширение воздуха в пузырьке может происходить либо изотермически, либо адиабатически. Поскольку размер пузырька определяют условия гидростатики и силы Стокса, то принимаем расширение воздуха в пузырьке как изотермическое, поэтому размеры пузырька должны быть достаточно малыми.
Запишем условие для изотермического процесса при вертикальном всплытии пузырька воздуха:
где p — давление жидкости, Па; V — объём жидкости, м³.
Если p0 — атмосферное давление [Па], то давление на глубине h [м] в жидкости плотностью ρ [кг/м³] будет равно (p0 + ρgh), где g — ускорение свободного падения, g = 9,81 м/с2; ρ — плотность жидкости, кг/м³; h — глубина, м.
Согласно закону изотермического расширения пузырька (2) на глубине слоя жидкости найдём радиус пузырька:
где r0 — радиус пузырька на поверхности воды, мм.
Пузырёк движется со скоростью v в жидкости, характеризуемой динамической вязкостью [Па·с]. Движение сферического пузырька в жидкости, которая рассматривается как непрерывная среда, и размеры которого (пузырька) значительно превышают размеры молекул среды, описывается уравнением Стокса для вязкого сопротивления:
где Fc — сила Стокса, Па; м — динамическая вязкость, Па·с или Н·с/м²; v — скорость всплытия пузырька, м/с.
Сила Архимеда Fа (подъёмная сила для пузырька) определяется из выражения
и она равна силе Стокса.
Сила тяжести равна:
где m — масса пузырька, кг.
Сила тяжести зависит от геометрических размеров пузырька. Эта сила крайне мала в сравнении с силами, действующими на пузырёк воздуха в воде, следовательно, значением силы тяжести можно пренебречь.
Скорость всплывания пузырька находится по уравнению:
От шарообразной формы переходим к изменению форм пузырька [2, 3].
Пузырёк находится в движении во время подъёма до поверхности воды. При этом пузырёк воздуха принимает шарообразную форму за счёт действия сил поверхностного натяжения.
Кроме того, изменение давлений сред (внутренней и внешней) пузырька приводит к деформации его поверхности, что способствует колебанию пузырька.
Применительно к единичному всплывающему пузырьку, на границе раздела фаз возникает разность давлений Δр, описываемая уравнением:
где р1 и р2 — давления двух фаз на глубине, Па; σ1,2 — поверхностное натяжение на границе двух фаз, Н/м; Rк — радиус кривизны поверхности рассматриваемого пузырька, м.
В результате увеличения объёма и изменения формы пузырька возникают его колебательные движения. Траектория всплытия пузырька принимается смещающейся относительно вертикали и носит волновой характер (рис. 2).
Теперь известны все величины, определяющие силу Стокса, что позволяет вычислить работу, совершаемую всплывающим пузырьком.
Вертикальное направление всплывания пузырька выберем за ось Oy.
Увеличение размеров и изменение формы пузырька передаётся окружающей пузырёк жидкости. Тем самым возникает суммарная работа dA и приращение свободной энергии согласно силам, действующим на пузырёк (рис. 1).
Поэтому приращение свободной энергии du в пересчёте на один пузырёк определится равенством:
где du и dA выражаются в джоулях (Дж).
Используя в формуле (9) выражения для силы Стокса (4), радиуса пузырька (3) и скорости всплытия пузырька (7), получаем следующий результат:
Для расчёта свободной энергии пузырьков введём функцию распределения f (r), которая представляет собой плотность вероятности обнаружения размера пузырька в единичном объёме между пузырьками с радиусами r и (r + dr).
Количество пузырьков с такими размерами в объёме dV будет равно f (r)drdV, поэтому их вклад в свободную энергию запишется как:
Помня, что V0 = 4/3(πr0 3 ), и интегрируя по всем возможным размерам пузырьков, получаем:
здесь r_ 03 — среднее значение куба радиуса пузырька на уровне поверхности жидкости, мм³; количество пузырьков в единице объёма жидкости, шт.
Термодинамическая связь параметров системы определяет давление р в системе как производную свободной энергии по объёму. Избыточное давления жидкости тогда составит:
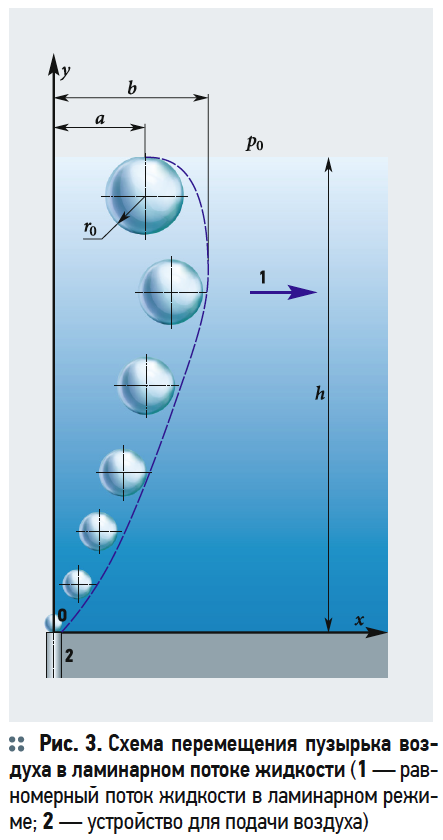
Рассмотрим всплытие пузырька воздуха в потоке жидкости при ламинарном режиме течения.
На рис. 3 представлена схема воздействие потока жидкости на вертикальное всплывание пузырька воздуха. Под воздействием распределения скоростей потока v = f(h) происходит смещение пузырька от вертикальной оси Oy. Согласно основным законам гидродинамики распределение скоростей зависит от кинетической энергии потока [3, 4]. По сечению потока происходит распределение скоростей, которые зависят от сопротивления между слоями жидкости при движении.
Нижние слои потока имеют сопротивление движению за счёт шероховатости дна, а движение верхнего слоя замедляется на границе раздела фаз «вода-воздух».
Обозначим через a [мм] расстояние от оси Oy до всплывшего пузырька на поверхности жидкости, а через b [мм] расстояние от оси Oy до всплывающего пузырька, максимально сместившегося по направлению движения жидкости.
Разница между a и b всплывающего пузырька зависит от скорости потока. Тогда выражение (14) запишется как
Полученная математическая зависимость позволяет более точно осуществить численные эксперименты на определённом этапе проектирования аэрационных сооружений систем водоочистки.
Эти действия направлены на нормализацию неустойчивости работы аэрационных сооружений и на определение оптимальных условий технологического процесса.
Выводы
1. Произведён анализ воздействия физических факторов на движение пузырька воздуха в воде, основанный на изотермическом процессе.
2. Получено уравнение, в котором приводится термодинамическая связь в определении давления в системе, как производная свободной энергии в потоке воды с учётом гидродинамических отклонений.
3. Использование полученного выражения позволяет повысить эффективность процесса водоочистки с применением аэрации.
Источник
Дайвер пускает «мыльные пузыри» под водой и снимает захватывающие дух результаты
Как же мы порой любим наблюдать за творчеством изобретательных людей, ведь они делают нашу жизнь чуть красочнее и разнообразнее.
На сей раз предлагаю вам получить заряд хорошего настроения, познакомив с интересными фотографиями от дайверов. На снимках выстроены увлекательные зарисовки, где главные роли отведены молодым людям и… воздушным кольцам.
Креативная задумка
Группа друзей решила оригинальным способом сохранить воспоминания об отдыхе на побережьях Гавайев и Каймановых островов. Погружаясь под воду, ребята начинали пускать парящие колечки, которые чем-то напоминали мыльные пузыри, и делали их частью своих мини-композиций. За запечатление незабываемых кадров отвечал британец Марк Тилли.
Забавное фото с воздушным обручем в виде нимба.
Здесь дайверу Жану Луи Лебре понадобился дополнительный инвентарь в виде 2-х пальмовых ветвей.
Вот девушка грациозно ступает по череде невесомых пузырей за секунду до того, как они распадутся на множество воздушных горошин и устремятся к поверхности.
Кортни Стаффорд пошла еще дальше и создала 2 большие левитирующие петли. Такие элементы формируются при слиянии нескольких кружочков.
А тут петля дополнена ровным кольцом.
Друзья с теплотой вспоминают совместные путешествия, рассматривая столь яркую подборку изображений.
Методика выполнения
На первом этапе необходимо максимально наполнить легкие воздухом и опуститься на несколько метров под воду. Далее следует постараться принять горизонтальное положение тела и приступить непосредственно к трюку. Важно следить за расходом кислорода и не тратить его понапрасну.
Теперь нужно, плотно сомкнув губы, высунуть язык и с силой вытолкнуть пучок воздуха наружу (в результате этого действия язык вновь окажется в ротовой полости). Чем больше легкие вместят в себя кислорода, тем больше колечек получится сотворить.
На видео в деталях представлен описанный процесс:
Если 2 и более воздушных обруча соприкоснутся друг с другом, получится длинная петля.
Помните, что цикл жизни подобных элементов невелик – всего несколько секунд. Поэтому для получения качественного фото понадобится некоторая сноровка.
Источник