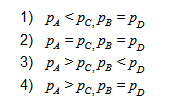Высота столба зависимость вода давление

Статика. Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление).

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то дав­ление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидроста­тическим.

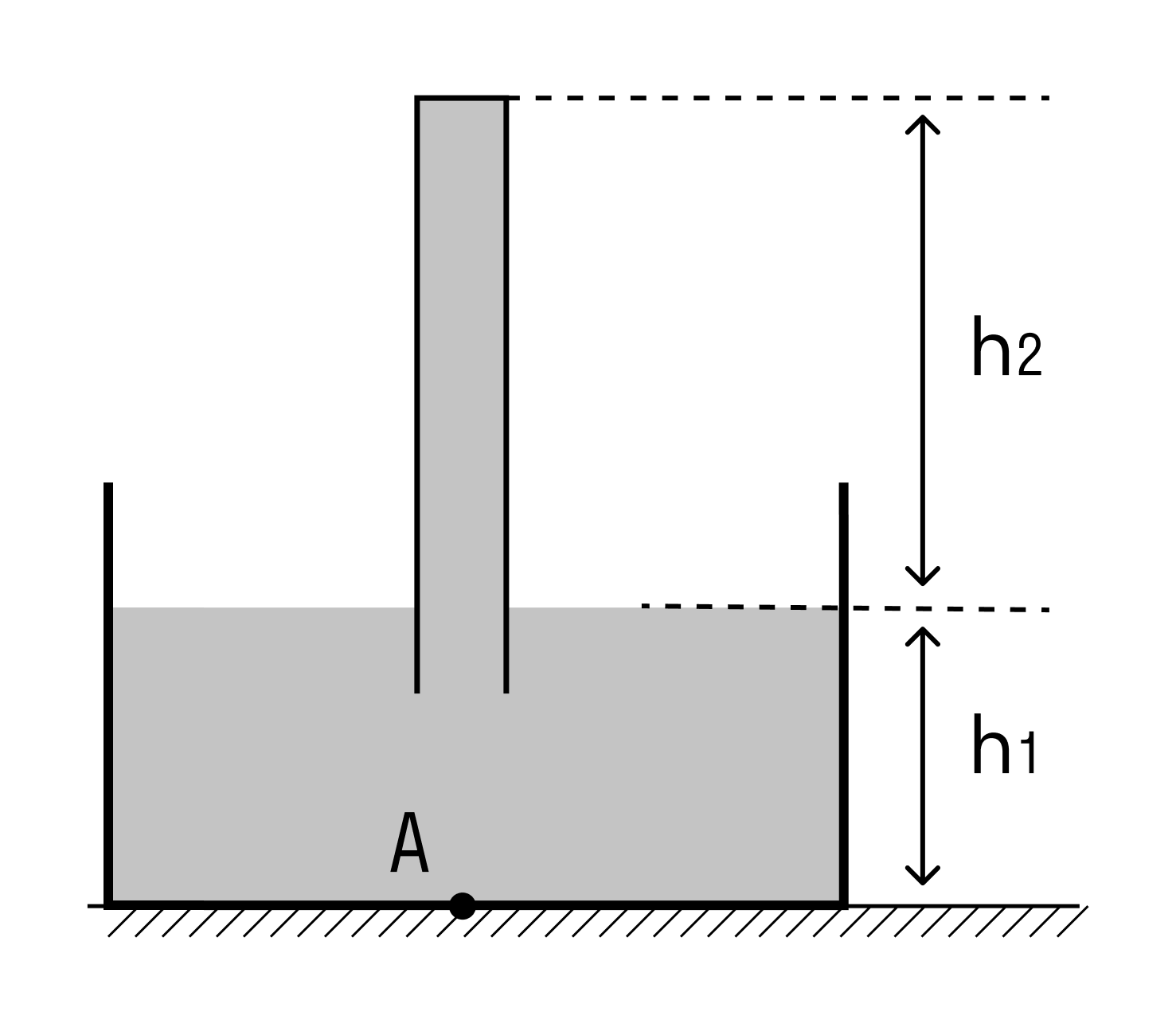
Получим формулу для расчета гидростатического давления жидкости на произвольной глубине h (в окрестности точки A на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления p в основании этого столба на площадь его сечения S:

2) как вес того же столба жидкости, т. е. произведение массы m жидкости на ускорение сво­бодного падения:

Масса жидкости может быть выражена через ее плотность p и объем V:

а объем — через высоту столба и площадь его поперечного сечения:

Подставляя в формулу (1.28) значение массы из (1.29) и объема из (1.30), получим:

Приравнивая выражения (1.27) и (1.31) для силы давления, получим:

Разделив обе части последнего равенства на площадь S, найдем давление жидкости на глубине h:

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободно­го падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе, давление на стенки сосуда, а так­же давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

Гидростатический парадокс .

Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

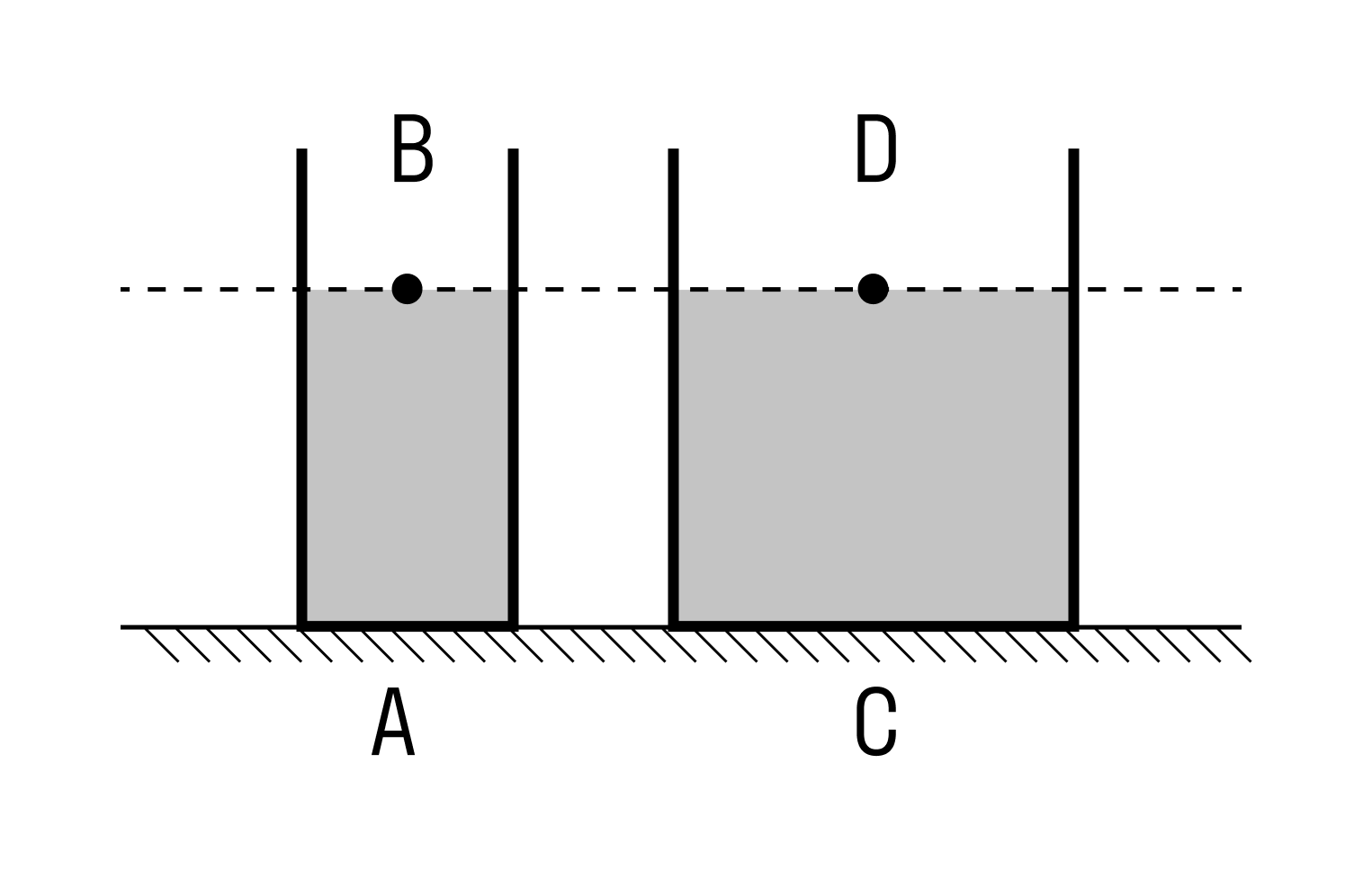
Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужа­ющихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: p = pgh (формула гидростатического давления жидкости). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосу­дов, одна и та же. Она равна весу вертикального столба ABCD жидкости: P = oghS, здесь S — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способ­ностью жидкости передавать давление одинаково во всех направлениях.

Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное дав­ление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давле­ние. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, подняв­шись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давле­ние в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Источник

Гидростатическое давление

Калькулятор находит неизвестные величины по заданным, используя формулу давления столба жидкости.

Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:

Калькулятор позволяет найти

• давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
• высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
• плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
• ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости

Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения — земное ускорение, и для давления — величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.

Гидростатическое давление

Гидростатическое давление — давление столба воды над условным уровнем.

Формула гидростатического давления выводится достаточно просто

Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
В 1648 г. это продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Также это приводит к такому явлению как гидростатический парадокс.

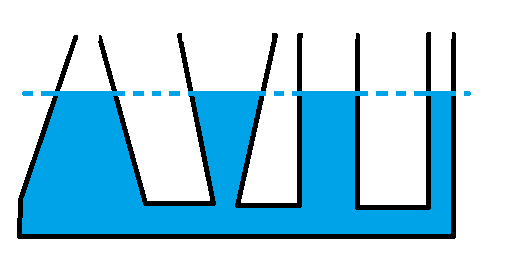
Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.

На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда

Источник

Закон Паскаля

О чем эта статья:

Давление

Идущий по рыхлому снегу человек будет в него постоянно проваливаться. А вот на лыжах он сможет передвигаться по тому же самому снегу спокойно. Казалось бы, ничего не меняется — человек воздействует на снег с одинаковой силой и на лыжах, и без них.

Дело в том, что «проваливание» в снег характеризуется не только силой — оно также зависит от площади, на которую эта сила воздействует. Площадь поверхности лыжи в 20 раз больше площади поверхности подошвы, поэтому человек, стоя на лыжах, действует на каждый квадратный сантиметр с силой в 20 раз меньшей, чем без них.

Или, например, если вы будете с одинаковой силой втыкать кнопки в пробковую доску, легче войдет та кнопка, у которой более заостренный конец, так как его площадь меньше.

Резюмируем: результат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади поверхности, к которой эта сила приложена.

А теперь подтвердим этот вывод опытами, как настоящие физики.

Возьмем небольшую доску и вобьем гвозди в ее углы. Также возьмем емкость с песком и поставим конструкцию из доски и гвоздей в эту емкость. Сначала расположим конструкцию шляпками вниз и поставим на нее гирю. Конструкция не утонет в песке, а только чуть-чуть углубится в него.

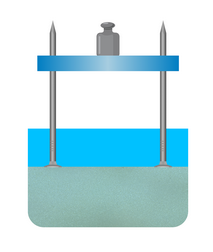
Затем перевернем конструкцию так, чтобы шляпки гвоздей оказались сверху и также поставим на доску гирю. Теперь конструкция утонет в песке.

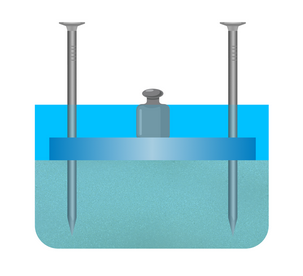
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия силы.

Во всех примерах мы говорили о действии силы, перпендикулярной поверхности. Чтобы охарактеризовать это действие, используется величина давление.

Давление

p = F/S

p — давление [Па]

F — сила [Н]

S — площадь [м 2 ]

Как уменьшить или увеличить давление

Тяжелый гусеничный трактор производит давление на почву, равное 40–50 кПа. Мальчик массой 45 кг производит давление всего лишь в 3 раза меньше, чем такой трактор. Это связано с большой площадью гусениц трактора.

В зависимости от того, какое давление хотят получить, площадь опор уменьшают или увеличивают. Например, чтобы уменьшить давление здания на грунт, в процессе строительства увеличивают площадь нижней части фундамента.

Шины грузовых автомобилей делают значительно шире легковых автомобилей. Чтобы убедиться в этом, обратите внимание на колеса какой-нибудь большой фуры. Самые широкие шины можно увидеть на автомобилях, предназначенных для передвижения в пустыне. Тот же лайфхак используется в шасси самолетов.

Обратную зависимость тоже применяют, например, при создании лезвий колющих и режущих инструментов. Острое лезвие имеет малую площадь, поэтому даже при небольшом нажатии создается большое давление.

Задачка раз

Книга лежит на столе. Масса книги равна 0,6 кг. Площадь ее соприкосновения со столом равна 0,08 м2. Определите давление книги на стол.

Решение

На стол будет давить сила, равная весу книги. Так как она покоится, ее вес будет равен силе тяжести. Следовательно:

p = mg/S = 0,6 × 10 / 0,08 = 75 Па

Ответ: давление книги на стол будет равно 75 Па.

Задачка два

Гусеничный трактор ДТ-75М массой 6 610 кг имеет опорную площадь обеих гусениц 1,4 м 2 . Определите давление этого трактора на почву.

Решение:

p = mg/S = 6 610 × 10 / 1,4 = 47 214 Па = 47,2 кПа

Ответ: давление трактора на почву составляет 47,2 кПа.

Задачка три

Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см2. Какое давление человек оказывает на пол?

Решение

Масса человека: m = 80 кг.

Вес сумки, которую держит человек: P_c = 100 Н.

Площадь соприкосновения подошвы ботинок с полом: S = 600 см 2 .

600 см 2 = 600 / 10 000 м 2 = 0,06 м 2

Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:

Поэтому давление, оказываемое человеком с сумкой на пол, равно:

p = (mg + P_с) / S = (80 × 10 + 100) / 0,06 = 15 000 Па = 15 кПа

Ответ: давление человека с сумкой на пол равно 15 кПа.

Определение закона Паскаля

Итак, мы подошли к формулировке закона Паскаля, и звучит она так:

Давление, производимое на жидкость или газ, передается в любую точку одинаково во всех направлениях.

Обратите внимание — закон работает только с жидкостями и газами. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел. Если молекулы жидкости и газа движутся почти свободно, то молекулы твердых тел так не умеют. Они могут лишь колебаться, немного отклоняясь от исходного положения. Именно благодаря свободному передвижению молекулы газа и жидкости оказывают давление во всех направлениях.

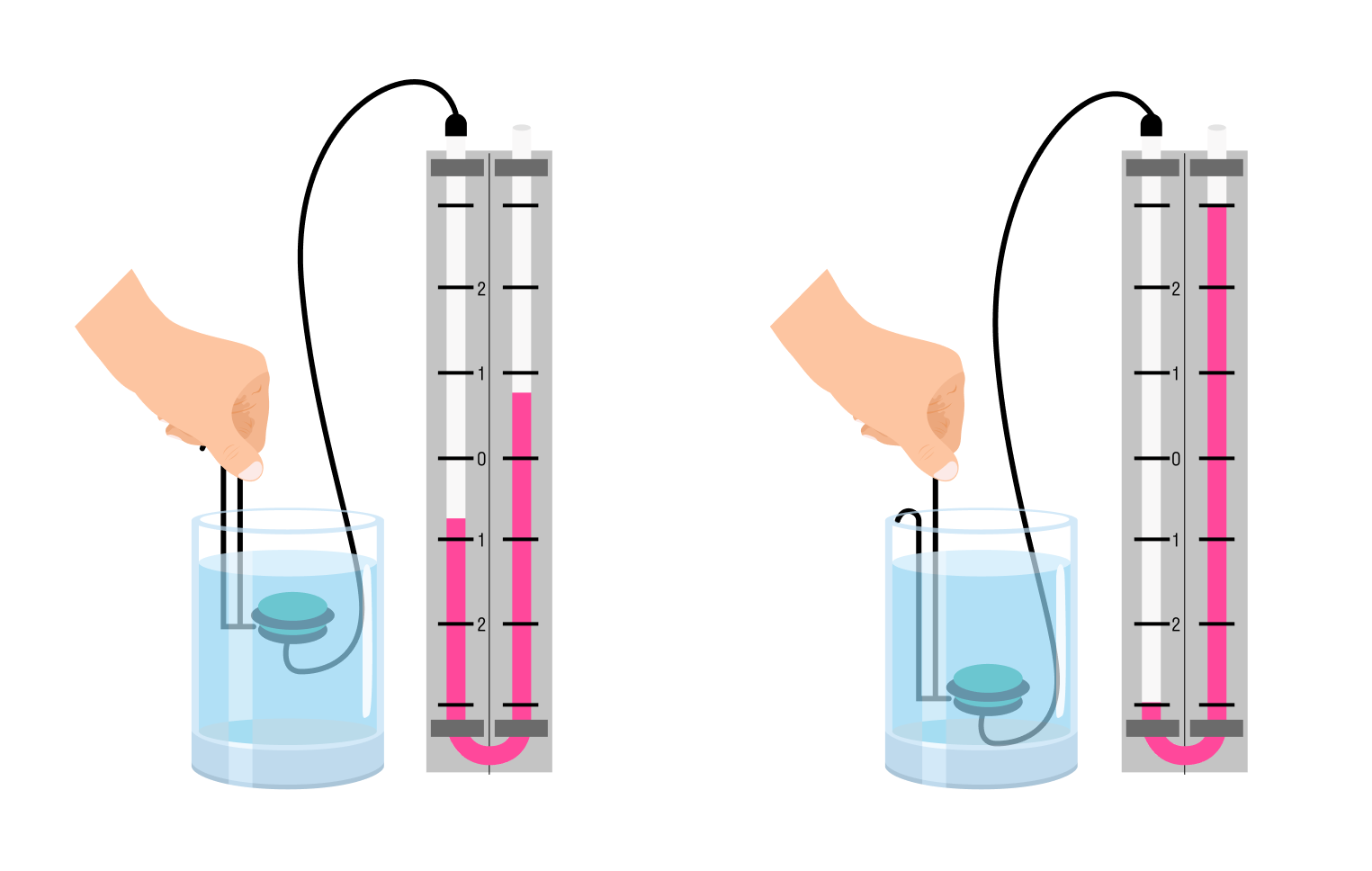
Рассмотрим опыт с шаром Паскаля, чтобы стало понятнее.

Присоединим к трубе с поршнем полый шар со множеством небольших отверстий. Зальем в шар воду и будем давить на поршень. Давление в трубе вырастет и вода будет выливаться через отверстия, причем напор всех струй будет одинаковым. Такой же результат получится, если вместо воды в шарике будет газ.

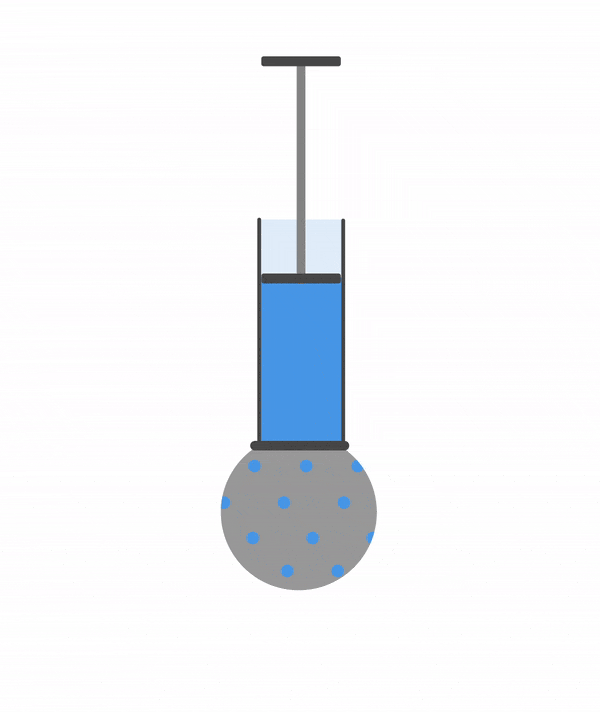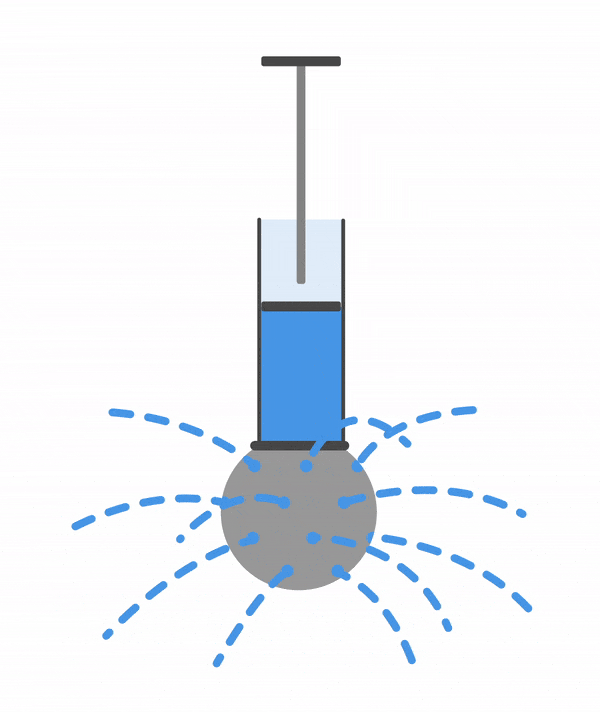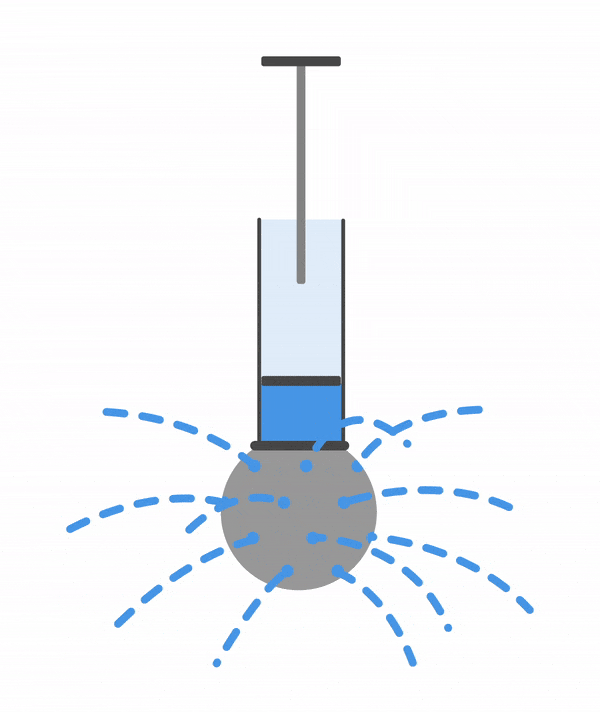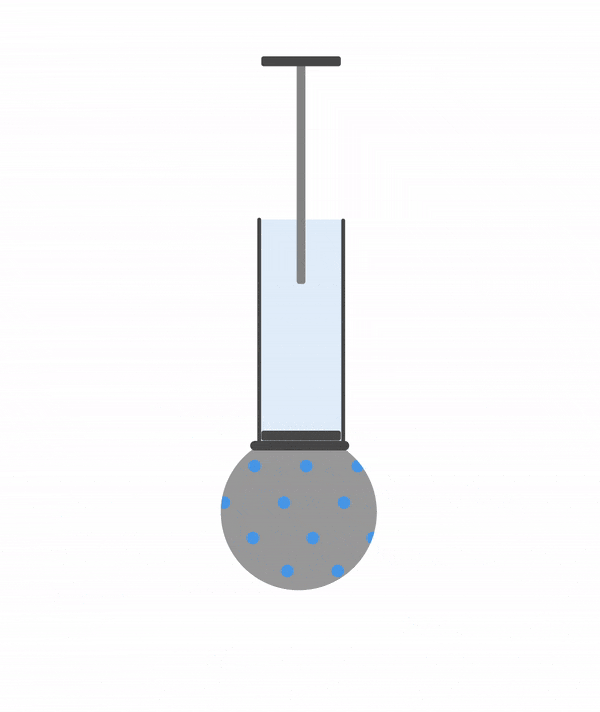
Давление жидкости

Из закона Паскаля следует, что раз давление передается одинаково во всех направлениях, то верхние слои жидкости давят на средние, средние — на нижние, нижние — на дно сосуда.

Давление внутри жидкости на одном и том же уровне одинаково по всем направлениям. С глубиной давление увеличивается.

Это утверждение проверяется с помощью манометра — прибора для измерения давления. Чем глубже мы измеряем давление, тем больше показания.

Давление столба жидкости

p = ρgh

ρ — плотность [кг/м 3 ]

h — высота столба жидкости [м]

g — ускорение свободного падения [м/с 2 ]

На Земле g = 9,8 м/с 2

Формула давления столба жидкости часто требуется в задачах.

Задачка раз

На горизонтальном столе стоят два цилиндрических сосуда — узкий и широкий (см. рисунок). В узкий сосуд налита вода, в широкий — керосин. Уровень жидкости в сосудах одинаковый. Сравните давления p жидкостей в точках A, B, C, D и выберите правильную пару утверждений.

Решение

Давление столба жидкости прямо пропорционально ее плотности и высоте столба. Плотность воды больше плотности керосина, следовательно, давление в точке A больше давления в точке C. Давления в точках B и D равны.

Правильный ответ указан под номером 4.

Задачка два

В сосуд с водой плотностью ρ = 998 кг/м 3 опущена вертикальная стеклянная пробирка, целиком заполненная водой (см. рисунок). Высота h₁ равна 0,3 м. Найдите давление, оказываемое водой на дно сосуда в точке А. Ускорение свободного падения примите равным 10 м/с 2 .

Решение

Поскольку вода не вытекает из пробирки, давление столба высотой h₂ на жидкость в сосуде высотой h₁ уравновешено давлением, которое оказывает вода в сосуде на столб воды в пробирке. Сосуд открытый, поэтому на него действует внешнее давление, которое и передается столбу воды. В результате столб воды в пробирке не оказывает дополнительного давления на точку А, поэтому давление, оказываемое водой на дно сосуда в точке А, равно p = ρgh1. Тогда:

p = ρgh₁ = 998 × 10 × 0,3 = 2 994 Па

Источник