За какое время остынет вода формула

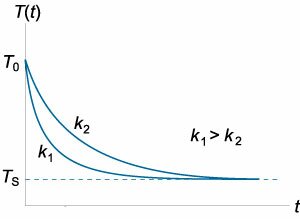
В конце \(17\) века британский ученый Исаак Ньютон изучал охлаждение тел. Эксперименты показали, что скорость охлаждения примерно пропорциональна разнице температур между нагретым телом и окружающей средой. Этот факт можно записать в виде дифференциального уравнения: \[\frac<><

> = \alpha A\left( <— T> \right),\] где \(Q\) − количество теплоты, \(A\) − площадь поверхности тела, через которую передается тепло, \(T\) − температура тела, \(<>\) − температура окружающей среды, \(\alpha\) − коэффициент теплопередачи , зависящий от геометрии тела, состояния поверхности, режима теплопередачи и других факторов.

Поскольку \(Q = CT,\) где \(C\) − теплоемкость тела, то дифференциальное уравнение можно записать как \[\frac<

> = \frac<<\alpha A>>\left( <— T> \right) = k\left( <— T> \right).\] Решение данного уравнение имеет вид: \[T\left( t \right) = + \left( <— > \right)>,\] где \(\) обозначает начальную температуру тела.

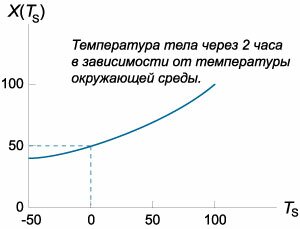
Таким образом, температура тела уменьшается экспоненциально по мере охлаждения, приближаясь к температуре окружающей среды. Скорость охлаждения зависит от параметра \(k = \large\frac<<\alpha A>>\normalsize\) ( коэффициента теплопроводности ). С увеличением коэффициента \(k\) (например, вследствие увеличения площади поверхности), тело будет охлаждаться быстрее (рисунок \(1\).)

Мы решим задачу сначала для случая произвольной температуры окружающей среды, а затем вычислим конечную температуру тела при температуре среды \(0^\circ.\)

Пусть начальная температура нагретого тела составляет \( = 200^\circ.\) Последующее изменение температуры описывается формулой: \[ + \left( <— > \right)> > = <+ \left( <200^\circ - > \right)>.> \] В конце первого часа тело охладилось до \(100^\circ.\) Следовательно, можно записать следующее соотношение: \[ \right) = 100^\circ = + \left( <200^\circ - > \right)>,>\;\; <\Rightarrow 100^\circ = + \left( <200^\circ - > \right)>.> \] Спустя \(2\) часа температура тела становится равной \(X\) градусов: \[X = + \left( <200^\circ - > \right)>.\] Таким образом, мы получили систему двух уравнений с тремя неизвестными: \(,\) \(k\) и \(X:\) \[\left\< \begin 100 = + \left( <200 - > \right)>\\ X = + \left( <200 - > \right)> \end \right..\] Мы не можем однозначно определить температуру тела \(X\) через \(2\) часа из данной системы. Однако можно вывести зависимость \(X\) от температуры окружающей среды \(.\) Выразим функцию \(>\) из первого уравнения: \[> = \frac<<100 - >><<200 - >>.\] Тогда \[> = <\left( <>> \right)^2> = <\left( <\frac<<100 - >><<200 - >>> \right)^2>.\] Следовательно, зависимость \(X\left( <> \right)\) имеет вид: \[ > \right) = + \left( <200 - > \right)<\left( <\frac<<100 - >><<200 - >>> \right)^2> > = <+ \frac<<<<\left( <100 - > \right)>^2>>><<200 - >>.> \] Если, например, положить температуру окружающей среды равной нулю, то температура тела через два часа будет составлять \[ = 0> \right) = 0 + \frac <<<<\left( <100 - 0>\right)>^2>>><<200 - 0>> > = <\frac<<10000>><<200>> = 50^\circ.> \] Зависимость температуры тела \(X\) от температуры окружающей среды в данной задаче показана выше на рисунке \(2.\)

Прежде всего, отметим разницу со случаем когда тело охлаждается в среде, температура которой постоянна. В этом случае температура тела формально будет бесконечно долго приближаться к температуре окружающей среды. В нашей же задаче температура среды линейно возрастает. Поэтому, рано или поздно температура тела станет равной температуре среды, то есть задача имеет решение. Будем считать также, что соблюдается квазистационарный режим, т.е. все переходные процессы в системе быстро затухают.

В таком случае процесс можно описать дифференциальным уравнением: \[\frac<

> = k\left( <— T> \right).\] По условию задачи, \( = > + \beta t.\) Следовательно, последнее уравнение можно записать в виде: \[ <\frac<

> = k\left( <> + \beta t — T> \right)>\;\; <\text<или>\;\;T’ + kT = k> + k\beta t.> \] Мы получили линейное дифференциальное уравнение, которое можно решить, например, с помощью интегрирующего множителя: \[u\left( t \right) = >> = >.\] Общее решение уравнения записывается в форме \[ >\left( > + k\beta t> \right)dt> + C>><<>>> > = <\frac<>\int <>dt> + k\beta \int <>tdt> + C>><<>>>.> \] Второй интеграл в числителе находится интегрированием по частям: \[ <\int <\underbrace <>>_\underbrace t_vdt> > = <\left[ <\begin<*<20>> >>\\ >>\\ \\ \end> \right] > = <\frac<1>>t — \int <\frac<1>>dt> > = <\frac<1>>t — \frac<1><<>>> > = <\frac<1>>\left( > \right).> \] Таким образом, закон охлаждения тела имеет следующий вид: \[ = <\frac<> \cdot \frac<1>> + k\beta \cdot \frac<1>>\left( > \right) + C>><<>>> > = <> + \beta t — \frac<\beta > + C>.> \] Постоянная \(C\) определяется из начального условия \(T\left( \right) = .\) Тогда \[C = — > + \frac<\beta >.\] Итак, процесс охлаждения тела описывается формулой \[T\left( t \right) = > + \beta t — \frac<\beta > + \left( <— > + \frac<\beta >> \right)>.\] В момент \(\tau,\) температуры тела и окружающей среды становятся равными друг другу: \[T\left( \tau \right) = > + \beta \tau .\] Время \(\tau\) определяется из уравнения: \[\require <\cancel<> + \beta \tau> = \cancel<> + \beta \tau> — \frac<\beta > + \left( <— > + \frac<\beta >> \right)>,>\;\; <\Rightarrow \left( <— > + \frac<\beta >> \right)> = \frac<\beta >,>\;\; <\Rightarrow \frac<\beta >\left( <— > + \frac<\beta >> \right) = >,>\;\; <\Rightarrow \frac<\beta >\left( <— >> \right) + 1 = >,>\;\; <\Rightarrow \tau = \frac<1>\ln \left[ <\frac<\beta >\left( <— >> \right) + 1> \right].> \] Мы можем сделать оценку времени \(\tau\) для некоторых типичных значений параметров: \[ <> = 20^<\circ>C,\;\;\;k = \frac<1><5>\,\text<мин>^<-1>,>\;\;\; <\beta = 2\,\frac<\text<град>><\text<мин>>,\;\;\; = 200^<\circ>C.> \] В результате получаем: \[ <\tau = \frac<1>\ln \left[ <\frac<\beta >\left( <— >> \right) + 1> \right] > = <\frac<1><<\frac<1><5>>>\ln \left[ <\frac<<\frac<1><5>>><2>\left( <200 - 20>\right) + 1> \right] > = <5\ln \left[ <\frac<1><<10>> \cdot 180 + 1> \right] > = <5\ln 19 >\approx <5 \cdot 2.944>\approx <14.77\left[ <\text<мин>> \right].> \]

Источник

Время охлаждения (нагрева)

Нестационарный режим теплообмена – это режим, когда температура тел или сред, участвующих в процессе обмена тепловой энергией изменяется во времени. При этом время охлаждения (нагрева) – это аргумент функции температуры тела. Зависимость температуры от времени.

. характеризуется скоростью теплового обмена, которая пропорциональна разности температур тела и окружающего пространства. В отличие от стационарного режима, при котором температуры всех точек системы остаются неизменными длительное время, нестационарный теплообмен возникает, например, при помещении тела в среду с более низкой или более высокой температурой. Если среда – это условно бесконечное пространство (например, атмосферный воздух или вода в «большой» ёмкости), то влияние тела на температуру среды ничтожно, поэтому охлаждение (нагрев) тела происходит при условно постоянной температуре окружающего газа или жидкости.

Заметим, что охлаждение тела сточки зрения математики – это нагрев со знаком «минус». И нагрев, и охлаждение описываются одними и теми же формулами!

О каких задачах может идти речь? Представим небольшой перечень вопросов, на которые можно попытаться ответить, используя предложенный далее расчет в Excel:

Сколько времени будет нагреваться деталь в печи?
Сколько времени остывает отливка после выбивки из формы?
Сколько времени требуется для нагрева воды в бочке на даче?
Через какое время перемерзнет наружный водопровод при отсутствии разбора?
Сколько времени нужно на охлаждение банки пива в холодильнике?

Расчет в Excel времени охлаждения (нагрева).

Алгоритм расчета базируется на законе Ньютона-Рихмана и на теоретических и практических исследованиях регулярного теплового режима советскими учеными Г.М. Кондратьевым («Регулярный тепловой режим», Москва, 1954г.) и М.А. Михеевым («Основы теплопередачи», Москва, 1977 г.).

Для примера выбран расчет времени нагрева до +22 °C в комнате с температурой воздуха +24 °C пивной алюминиевой банки с водой, предварительно охлажденной до +13 °C.

Исходные данные:

Параметров, необходимых для выполнения расчета времени охлаждения (нагрева) – 12 (см. скриншот).

Ориентировочные сведения о значениях коэффициента теплоотдачи α приведены в примечании к ячейке D3.

Теплофизические характеристики материала тела λ, a, ρ, c легко можно найти в справочниках или по запросу в Интернете. В нашем примере – это параметры воды.

В принципе, для выполнения расчета достаточно знать значения любой из пар характеристик: λ, a или ρ, c. Но для возможности выполнения проверки и минимизации вероятности ошибки рекомендую заполнить значениями все 4 ячейки.

Вводим значения исходных данных в соответствующие ячейки листа Excel и считываем результат: нагрев воды от +13 °C до +22 °C в спокойном воздухе комнаты с постоянной температурой +24 °C будет длиться 3 часа 25 минут.

Для справки в самом конце таблицы вычислено время нагрева без учета формы тела – 3 часа 3 минуты.

Алгоритм расчета:

13.1. F=2·H·L+2·B·L+2·H·B – для параллелепипеда;
13.2. F=π·D·L+2·π·D2/4 – для цилиндра;
13.3. F=π·D2 – для шара.
14.1. V=H·L·B – для параллелепипеда;
14.2. V=L·π·D2/4 – для цилиндра;
14.3. V=π·D3/6 – для шара.
15. G=ρ·V
16.1 K=((π/H) 2+(π/L) 2+(π/B) 2 ) -1 – для параллелепипеда;
16.2 K=((2,405/(D/2)) 2+(π/L) 2 ) -1 – для цилиндра;
16.3 K=((D/2)/π) 2 – для шара.
17. m_∞=a/K
18. Bi=α·K·F/(λ·V)
19. Ψ=(1+1,44·Bi+Bi2) -0,5
20. M=Ψ·Bi
21. m_αλ=M·m_∞
22. m_cρ=Ψ·α·F/(c·ρ·V)
23. Δ=ABS (1-m_αλ/m_cρ)·100
24. t=(LN (ABS (t_c-t₁)) -LN (ABS (t_c-t₂))/m_αλ
25. t_N=(LN (ABS (t_c-t₁)) -LN (ABS (t_c-t₂)))·c·ρ·V/(α·F)

Проверка расчета опытом.

Как не трудно догадаться такой несколько странный пример выбран не случайно, а для возможности проведения простого опыта и последующего сравнения результатов. Были взяты термометр, часы и произведены замеры температуры воды в банке в процессе нагревания. Результаты расчетов и опыта отражены на графиках.

Результаты проведенного опыта показали, что нагрев банки с водой от +13 °C до +22 °C в комнате (+24 °C) продолжался примерно 3 часа 20 минут. Это на 5 минут меньше расчетного времени по Кондратьеву и на 17 минут дольше времени по классическому закону Ньютона-Рихмана.

Близость результатов и радует, и удивляет. Но не стоит переоценивать полученные итоги! Время охлаждения (нагрева), вычисленное по предложенной программе расчета в Excel, можно использовать лишь для приблизительных оценок продолжительности процессов! Дело в том, что принятые в расчете константами теплофизические характеристики тела и коэффициент теплоотдачи таковыми на самом деле не являются. Они зависят от изменяющейся температуры! К тому же регулярный режим теплообмена устанавливается не сразу после помещения тела в среду, а спустя какое-то время.

Обратите внимание, что полученные из опыта значения температур банки с водой в течение первого часа расположены выше теоретической расчетной кривой (см. графики). Это означает, что коэффициент теплоотдачи в этом периоде времени был больше выбранного нами значения α=8,3 Вт/(м 2 ·К).

Определим среднее значение α в первые 58 минут из результатов опыта. Для этого:

Запишем t₂=17,5 °C в ячейку D6.
Активируем («встанем мышью») ячейку D28.
Выполним: Сервис – Подбор параметра.
И установим в D28 значение 58 минут, изменяя ячейку D3.

α=9,2 Вт/(м 2 ·К).

Проделав ту же процедуру для t₂=22,5 °C и t=240 мин, получим α=8,3 Вт/(м 2 ·К).

Выбранное при теоретическом расчете значение α (по рекомендации СП 50.13330.2012 и формуле из Справочника по физике – см. примечание к ячейке D3) чудесным образом, хотя и совершенно случайно, совпало со значением α, вычисленным по опытным данным.

Рассмотренным способом можно определять реальные точные средние значения коэффициента теплоотдачи тел с любой формой поверхности по практическим замерам всего двух значений температуры тела и промежутка времени между этими замерами.

Остается добавить, что температура банки с водой после рассмотренных 4-х часов в последующее время будет асимптотически приближаться к 24 °C.

Прошу уважающих труд автора скачивать файл с программой расчетов после подписки на анонсы статей!

Ссылка на скачивание файла: vremya-ohlazhdeniya (xls 55,5KB).

Так сколько часов составит время охлаждения алюминиевой банки с пивом 0,45 л от +20 °C до +8 °C в холодильнике (+3°C)? По расчету в программе – 2,2…2,4 часа. Опытом не проверял… 🙂

Любопытный (возможно, только для меня) факт обнаружился при работе над статьей. И у куба с размером ребер a, и у цилиндра с диаметром а и длиной а, и у шара с диаметром а отношение объема к площади поверхности одинаковое: V/F=a/6.

Статьи с близкой тематикой

Отзывы

53 комментария на «Время охлаждения (нагрева)»

Александр, спасибо за Ваши статьи и таблицы, но меня интересуют расчеты водяных колес в EXCEL и эту тему Вы почему-то обходите стороной.

Например колесо Диам.2 м. ширина 3м, скорость течения 2м/сек. -какова мощность на валу.

Спасибо! Весьма интересные выкладки. Я уже более 40 лет занимаюсь теплотехническими расчетами (нач. КБ печей, УВЗ) и эта тема — моя жизнь)))

Николай, Владимир спасибо за комментарии.

Ответ на Ваш вопрос, Николай:

1. Допустим колесо погружено в поток воды на 0,5м. Тогда масса воды за 1с = 0,5м*3м*2м/с*1000кг/м3=3000кг/с.

2. Энергия потока воды отбираемая из реки вашим колесом: T=m*v^2/2=3000*2^2/2=6000Дж.

3. Мощность подведенная к колесу: N=T/t=6000/1=6000Вт.

4. Если КПД вашей передачи (нужно посчитать) = 0,5. 0,7, то мощность на валу генератора Nг=3,0. 4,2КВт.

5. Мощность на валу колеса при соответствующем конструктиве, хорошей балансировке и подшипниках качения может быть более 5,5КВт.

Подробно о вышесказанном написано у меня применительно к воздуху вот здесь.

Благодарю Вас за статьи и расчеты. Очень полезное дело для пользы всех. Найти нужные расчеты тяжело и иной раз не представляется возможным.

Александр, большое спасибо за Ваши статьи!

У меня вопрос по воздушным теплообменникам (рекуператорах), используемых в системах вентиляции.

Какая скорость нагрева воздуха проходящего между пластинами алюминиевого теплообменника? Насколько я понимаю, процесс зависит от режима воздушного потока (турбулентный, ламинарный)?

Константин, на Ваш вопрос могу сказать только одно — нужно считать в каждом конкретном случае.

А поток для увеличения коэффициента теплоотдачи должен быть турбулентным. В теплообменниках для этого поверхности делают с «волнистостью» и специальными «завихрителями».

Спасибо Вам за публикации. Все доступно и понятно. Вы экономите гору времени и усилий!

Добрый день уважаемый Александр. Прошу Вас помочь рассчитать время нагрева бытового 12-ти литрового газового баллона с газом: вес стального баллона 6 кг, вес с СУГ 12.34 кг, исходная температура баллона с газом -37 гр. Цельсия до температуры +25 гр. Цельсия. Температура в помещении куда занесли баллон +25 гр. Цельсия. За какое время баллон согреется до температуры помещения + 25 гр. Цельсия. С Уважением Кузнецов Владимир.

Здравствуйте, уважаемый Владимир.

Я не знаю теплофизических характеристик СУГ, необходимых для выполнения расчета. Поищите их в интернете и пришлите мне, или сами посчитайте, скачав файл с расчетной программой.

(Теплофизические характеристики СУГ сильно зависят от температуры и давления, что существенно усложняет расчеты. Еще необходимо учитывать, что часть СУГ находится в жидкой фазе, а часть в газообразной. И по мере нагрева массовое соотношение фаз изменяется.)

Как высчитать скорость воздушного потока в тонкой стекляной трубке, при которой проходящий воздух будет полностью остывать?

Написать уравнения (похоже, дифференциальные) и решить систему.

Попытался посчитать охлаждение двигателя ДВС 1,5 литра на морозе от +60 до -10 при температуре 30

Пришлите через страницу «Обратная связь» файл. Посмотрю, что «не получилось».

Очень интересная статья. Увлекся я созданием простых приборчиков, программу написал для управления нагревом электронных плат лампами накаливания и все бы было хорошо если бы не инерционность. Для достижения температуры в 160 градусов я отключаю нагрев на 155, но это допустим при температуре в комнате в 26 градусов. Если же температура окружающей среды меняется то программа не может попасть в нужную температуру (она у меня примитивная). Есть ли простая формула для коррекции температуры отключения нагрева или легче опытным путем создать таблицу с нужными значениями?

Максим, проще и правильнее и точнее опытным путем создать таблицу. А затем данные таблицы аппроксимировать и получить простую формулу, которую можно «забить» в программу.

Теоретически сразу написать такую формулу очень сложно (практически невозможно) из-за необходимости описать все тела и пространство (геометрию, теплофизические характеристики, скорость и направление движения воздуха, . ), участвующие в теплообмене.

Спасибо за вашу публикацию.

Подскажите, пожалуйста, как рассчитать скорости охлаждения в сечениях на разных расстояниях от торца параллелепипеда при торцевой закалке?

Игорь, Вам необходимо выполнить расчет нестационарного температурного поля. Так как расчет может быть осуществлен только численными методами конечных элементов или конечных разностей, то ищите программу, так «вручную» это сделать не реально.

Например: apm.ru/thermal-analysis (нестационарная теплопроводность) бесплатно 30 дней. У них можно заказать выполнение расчета.

Может быть: temper3d.ru/temper-3d/ver-4/ Не знаю — нестационарный режим есть в ней или нет.

Статья очень понравилась, но возникли проблемы с расчетом нагрева объектов сложной формы. Можно ли менять объем и не скажеться ли это на расчет. Нужно посчитать время нагрева детали до 10 градусов, размещенную в теплое помещение, но она не может быть отнесена ни к чему, деталь сложной формы, зато можно определить ее объем по 3D модели.

Анна, для ориентировочной оценки времени охлаждения вашего тела смотрите п.25 расчета. Но погрешность может быть очень большой!

Лучше сделать так:

Посчитайте отношение объема вашего тела к его площади поверхности, а затем подберите эквивалентный цилиндр или параллелепипед с таким же отношением и таким же объемом.

Полезная программка, но есть вопрос. При рассчете тела большого объема разбег по 24 и 25 пункту больше чем на порядок. Цилиндр объемом 430м3, 11×4,5м tс=16, t1=22, t2=18. Какой результат ближе к истине?

Алексей, результаты в п.24 и п.25 разнятся только из-за критерия Ψ.

24. t=(LN (ABS (tc-t1)) -LN (ABS (tc-t2))/m

24. t=(LN (ABS (tc-t1)) -LN (ABS (tc-t2))·c·ρ·V/(α·F·Ψ)

25. tN=(LN (ABS (tc-t1)) -LN (ABS (tc-t2)))·c·ρ·V/(α·F)

При этом Ψ (0 0oC), коэф. теплопроводности Л, коэф. температуропроводности а, удельной теплоемкостью с проходит тело с пл.поверхности П и температурой Т (<<0оC) с скоростью V. При этом T<

Задача учебная или реальная? В любом случае не хватает данных:

— в какой среде находятся тела, её теплофизические параметры?

— какая форма тела №2?

— какие степени черноты поверхностей обоих тел?

— по какой траектории и на каком расстоянии проходит тело №2 относительно шара?

Если просто нужен вид кривой, то изобразить характер её изменения во времени — не трудно. Но для чего тогда перечислены в условии теплофизические параметры шара?

Добрый день, почему не могу скачать калькулятор?

Повторно, ну как скачать и пользоваться калькулятором, я подписался.

Нажимаете на ссылку и файл скачивается. Проверил только что — всё работает. Может у Вас защита на ПК от скачивания файлов xls?

Отправлю файл на почту.

Александр, спасибо за интересные статьи и расчеты.

Хоть и не занимаюсь теплотехникой (моя тема электротехника и электроника), но часто приходится разбираться в проблемах тепла тоже. Подчерпнул у вас много нового в этой теме.

Есть такая задача, оценить в течении какого времени температура в помещении поднимется с начальной до какой-то заданной, при работе в помещении тепловентилятора определенной мощности.

Конечно здорово было бы, что бы в расчете учитывался и теплообмен со стенами и с внешней средой, но в принципе хватило бы и простой оценки, как говорится с использованием «пары формул»).

Может быть посоветуете литературу или статью.

Еще раз спасибо!

Принцип решения Вашей задачи с использование «пары формул» изложен в статье на этом сайте:

Вам нужно определить время нагрева воздуха предметов и ограждающих конструкций (стен, полов, . ) в помещении при известной мощности теплового источника.

Советую также познакомиться с программой Agros2D (теплопередача, нестационарный анализ): agros2d.org.

Поможете рассчитать время, необходимое для охлаждения жидкости (сусло яблочное, используемое в дальнейшем для приготовления сидра) с 10 градусов до 2 градусов на улице при температуре воздуха минус 5 градусов.

Емкость диаметром 1,3 метра, высотой 2 метра, объем 2,5 куб. метра.

Очень приближенно при слабом ветре получается

9. 10 часов, может чуть больше.

Для яблочного сусла не нашел плотность и удельную теплоемкость, принял как для фруктового вина. Впрочем, для воды примерно тот же результат.

Читайте выше в комментариях от 16.06.2019:

«Если хотите более точно решить свою задачу, нужно произвести два замера температуры сусла t1 и t2 через какой-то промежуток времени t и таким образом опытным путем определить расчетный темп охлаждения:

m=(LN (ABS (tc-t1)) -LN (ABS (tc-t2))/t

А далее, зная m, легко решить задачу для любого другого t2 — найти время t по той же формуле (из п.24).»

Александр, добрый день!

Подскажите как в расчетный файл внести корректировки если у емкости расположенной на воздухе есть изоляция толщиной 150 мм и коэффициентом теплопроводности λ10 = 0,034 Вт/(м·К)

Этот приближенный расчет для твердых и однородных тел. Для жидкостей в больших емкостях годится лишь для грубых оценок, так как не учитывает конвективное перемешивание. Поэтому ответ:»Никак.»

Для оценки очень неплохой расчет и. наглядный для банки с пивом. Спасибо, что привели авторов по исследованию регулярных тепловых режимов.

Извините, дилетантский вопрос, насколько изменится время нагрева если изменить материал банки на стекло? Какие значения необходимо изменить в вашей таблице для правильного расчета? Учитывается ли масса материала банки?

Материал банки — алюминий — имеет большую теплопроводность, малую толщину и в расчете не участвует. По сути в примере выполнен расчет цилиндра из НЕПОДВИЖНОЙ воды (при отсутствии конвективного перемешивания).

Источник