Задача сосуды с водой решение

Логические задачи на переливания

Логические задачи на переливания с решением

Задача 1.

Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?

Задача 2.

Деление 10 л поровну, имея сосуды 3, 6 и 7 л.
Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 3.

Деление 8 л поровну, имея сосуды 8, 5 и 3 л.
Разделить на две равные части воду, находящуюся в полном 8 литровом сосуде, пользуясь этим и пустыми 5- и 3-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 4.

Деление 16 л поровну, имея сосуды 6, 11 и 16 л.
Разделить на две равные части воду, находящуюся в полном 16 литровом сосуде, пользуясь этим и пустыми 11- и 6-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 5.

Два сосуда и кран с водой.
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л?

Решения задач.

Решение задачи 1.

Наливаем кастрюлю.
Переливаем воду из кастрюли в банку.
Наливаем кастрюлю.
Доливаем полную банку, и в кастрюле остается 3 литра.

Решение задачи 2.

В скобках – второй вариант решения.

Сосуд 6 л	Сосуд 3 л	Сосуд 7 л
До переливания	4	0	6
Первое переливание	1 (4)	3 (3)	6 (3)
Второе переливание	1 (6)	2 (1)	7 (3)
Третье переливание	6 (2)	2 (1)	2 (7)
Четвертое переливание	5 (2)	3 (3)	2 (5)
Пятое переливание	5 (5)	0 (0)	5 (5)

Решение задачи 3.

Сосуд 8 л	Сосуд 5 л	Сосуд 3 л
До переливания	8	0	0
Первое переливание	3	5	0
Второе переливание	3	2	3
Третье переливание	6	2	0
Четвертое переливание	6	0	2
Пятое переливание	1	5	2
Шестое переливание	1	4	3
Седьмое переливание	4	4	0

Решение задачи 4.

Сосуд 16 л	Сосуд 11 л	Сосуд 6 л
До переливания	16	0	0
Первое переливание	10	0	6
Второе переливание	10	6	0
Третье переливание	4	6	6
Четвертое переливание	4	11	1
Пятое переливание	15	0	1
Шестое переливание	15	1	0
Седьмое переливание	9	1	6
Восьмое переливание	9	7	0
Девятое переливание	3	7	6
Десятое переливание	3	11	2
Одиннадцатое переливание	14	0	2
Двенадцатое переливание	14	2	0
Тринадцатое переливание	8	2	6
Четырнадцатое переливание	8	8	0

Решение задачи 5.

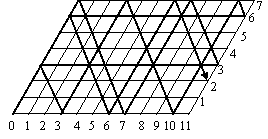
Если сначала наполнить 11-литровый сосуд, то потребуется 18 переливаний, а если 7-литровый, то, как следует из рисунка, – всего 14.

Логические задачи на переливания с решением

Источник

Задачи на измерение и взвешивание

Сосуды с водой I

Отмерьте ровно 4 литра, если у вас есть 3-литровая банка, 5-литровая банка и неограниченный доступ к воде.

Сосуды с водой II

Дано: 8-литровый сосуд, заполненный водой, и два пустых сосуда – объёмом 3 и 5 литров.
Как разделить воду на две равные части (4 и 4 литра), используя наименьшее количество переливаний?

Сосуды с водой III

Дано: 7-литровый сосуд, заполненный водой, и два пустых – объёмом 4 и 3 литра.
Поделите воду на 2, 2 и 3 литра, используя минимальное количество переливаний.

Сосуды с водой IV

Отмерьте 6 литров воды, используя 4 и 9-литровые сосуды.

Сосуды с водой V

Отмерьте 2 литра воды, используя:
1. 4 и 5-литровые сосуды;
2. 4 и 3-литровые сосуды.

1. Наполните 5-литровый сосуд водой.
   Перелейте из него в 4-литровый сосуд 4 литра и слейте всю воду из 4-литрового сосуда.
   Оставшийся в 5-литровом сосуде 1 литр перелейте в 4-литровый сосуд.
   Заново наполните 5-литровый сосуд водой и отлейте из него 3 литра воды в 4-литровый сосуд (где уже есть 1 литр).
   И тогда в 5-литровом сосуде останется 2 литра.
2. Тот же самый принцип, но всё в обратном порядке.
   Наполните водой 3-литровый сосуд и перелейте всю воду в 4-литровый сосуд.
   Заново наполните 3-литровый сосуд и из него отлейте воды в 4-литровый сосуд (туда влезет только 1 литр).
   В 3-литровом сосуде останется 2 литра.

Сосуды с водой VI

Даны 3 сосуда: сосуд А (8-литровый с 5-ю литрами воды); сосуд В (5-литровый с 3-мя литрами воды); и сосуд С (3-литровый с 2-мя литрами воды).
Отмерьте 1 литр, перелив воду только два раза.

Задача на взвешивание I

У вас 10 мешков с монетами, по 1000 монет в каждом. В одном из мешков все монеты фальшивые. Настоящая монета весит 1 г., фальшивая – 1,1 г.. Имея точные весы, как определить мешок с фальшивыми монетами с помощью только одного взвешивания?
Что если неизвестно, сколько мешков было с фальшивыми монетами?

Задача на взвешивание III

А эта задача ещё чуть посложнее предыдущей.
У вас есть 8 мешков с монетами по 48 монет в каждом. В пяти мешках настоящие монеты, а в остальных – фальшивые. С помощью одного взвешивания на точных весах определите все мешки с фальшивками, используя минимальное количество монет.

Задача на взвешивание IV

Один из 12-ти биллиардных шаров бракованный. Он весит или больше, или меньше, чем стандартный. У Вас есть чашечные весы-противовесы, на которых Вы можете сравнивать вес шаров.
Какое минимальное количество взвешиваний гарантирует нахождение бракованного шара?

Достаточно использовать весы три раза. Пометим шары числами от 1 до 12 и специальными символами:
x? означает, что о шаре x нам ничего неизвестно;
x означает, что этот шар может быть тяжелее остальных;
x. означает, что этот шар стандартный по весу.

Для начала на левую чашу положим шары 1? 2? 3? 4?, а на правую чашу шары 5? 6? 7? 8?. Если равновесия не достигнуто, то бракованный шар должен быть среди шаров под номерами 9-12. Теперь кладём на левую чашу 1.2.3. и на правую чашу 9?10?11? и смотрим на результат.

ЕСЛИ ДОСТИГНУТО РАВНОВЕСИЕ, то бракованным шаром является шар №12. Сравнив шар №12 с любым другим шаром, мы узнаем, легче ли он или тяжелее. Если левая чаша тяжелее, то шар №12 стандартен по весу, а 9 10> и 11> , и дальнейшие действия похожи на те, что свершались в предыдущем абзаце. Если левая чаша тяжелее, тогда 1> 2> 3> 4>, 5 2> 3> 5 9. 10. 11. Если достигнуто равновесия, то искомый шар – один из 6 . Сравним, к примеру, 1. и 4>. Если их вес одинаков, тогда шар №5 легче всех останьных шаров. В противном случае шар №4 тяжелее других (он ниже на чаше весов). Если левая чаша весов ниже, тогда все шары стандартного веса, за исключением 1> 2> и 3>. Определить, какой именно из них искомый бракованный шар – дело техники (описано в двух предыдущих абзацах (про 9

Задача на взвешивание V

На рождественской ёлке висят три пары шаров: два белых, два голубых и два красных. Внешне шары одинакового размера. Однако в каждой паре есть один лёгкий и один тяжёлый шар. Все лёгкие шары весят между собой одинаково, и так же все тяжёлые шары. С помощью двух взвешиваний на чашечных весах определите все лёгкие и все тяжёлые шары.

Задача на взвешивание VI

Имеется девять мешков: восемь с песком и один – с золотом. Мешок с золотом только чуть тяжелее. Вам даётся два взвешивания на чашечных весах, чтобы найти мешок с золотом.

Задача на взвешивание VII

Имеется 27 теннисных шариков. 26 весят одинаково, а 27-й чуть потяжелее.
Какое минимальное количество взвешиваний на чашечных весах гарантирует нахождение тяжёлого шарика?

Задача на взвешивание VIII

Купец уронил 40-фунтовую гирю, и она раскололась на 4 неравные части. Когда эти части взвесили, то оказалось, что вес каждой из них (в фунтах) — целое число. Более того, с помощью этих частей можно было взвесить на чашечных весах любой вес (представляющий собой целое число) до 40 фунтов.
Сколько весила каждая часть?

Песочные часы I

Как отмерить 9 минут с помощью 7-минутных и 4-минутных песочных часов?

Песочные часы II

Учитель математики использовал необычный метод измерения времени, отведённого на экзамен. У него были 7-минутные и 11-минутные песочные часы. И чтобы отмерить 15 минут, он переворачивал часы только 3 раза. Объясните как.
(Примечание: одновременное переворачивание обоих часов можно считать за одно переворачивание.)

Бикфордовы шнуры

Имеется два огнепроводных шнура, каждый из которых сгорает ровно за час. Однако шнуры горят неравномерно – некоторые их части горят быстрее, а некоторые медленнее.
Как с помощью этих шнуров отмерить ровно 45 минут?

Источник

Задача сосуды с водой решение

Краткая теория, используемая для решения задачи на сообщающиеся сосуды. Подробнее смотрите в конспекте «Сообщающиеся сосуды. Гидравлический пресс. Шлюзы».

Сообщающиеся сосуды — два или более соединённых между собой сосудов (ниже уровни жидкости), в которых жидкость может свободно перетекать из одного сосуда в другой.

Закон сообщающихся сосудов : в открытых сообщающихся сосудах любой формы при равновесии давление жидкости на любом горизонтальном уровне одинаково.

Схематически это выглядит таким образом, что в точках А и В ⇒ р _A = р _B .

ρ₁gh₁ + ρ₂gh₂ = ρ₃gh₃ + ρ₄gh₄

Обратите внимание! Ниже уровня, на котором находятся точки А и В, жидкость однородна. Обозначения : р — давление, ρ — плотность, h — высота, g — ускорение свободного падения (9,8 м/с^2).

Следствие 1 : в открытых сообщающихся сосудах при равновесии высоты столбов жидкостей, отсчитываемые от уровня, ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей.
Следствие 2 : в открытых сообщающихся сосудах при равновесии однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. В левом колене сообщающихся сосудов налита вода, в правом — керосин. Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.

Ответ: 0,04 м (или 4 см). Чтобы увидеть решение задачи, нажмите на спойлер ниже.

Задача № 2. В сообщающихся сосудах находятся ртуть и вода. Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?

Ответ: 0,85 м (или 85 см).

Задача № 3. В сообщающихся сосудах находятся ртуть, вода и керосин. Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?

Ответ: 0,335 м (или 33,5 см).

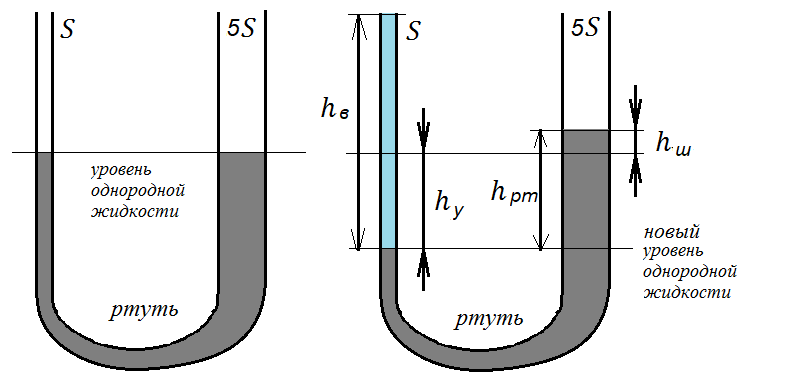
Задача № 4. В цилиндрических сообщающихся сосудах находится ртуть. Площадь поперечного сечения широкого сосуда в пять раз больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают воду, которая образует столб высотой 34 см. На сколько поднимется уровень ртути в широком сосуде и на сколько опустится в узком?

Ответ: в широком сосуде на 0,42 см, в узком — на 2,1 см.

Исходное положение уровня ртути показано на левом рисунке. Обозначим высоту, на которую поднялся уровень ртути в широком колене h_ш. Тогда объем этого столбика равен V = h_ш • 5S – так как площадь сечения широкого сосуда в пять раз больше, чем узкого.
Раз объем ртути в широком колене увеличился, то очевидно, что увеличился он за счет уменьшения объема в узком. Там высота столба ртути уменьшилась на высоту, точно соответствующую найденному объему. Раз сечение узкого колена меньше, чем широкого, то высота, на которую опустилась ртуть в узком сосуде, равна h_y = V/S = (h_ш • 5S)/S = 5h_ш.
Давление столба воды в левом колене равно давлению столба ртути над уровнем однородной жидкости в правом:
ρ_вgh_в = ρ_ртgh_рт. По рисунку мы можем выразить h_рт = h_ш + h_у и сократить уравнение на g:
ρ_вh_в = ρ_рт(h_ш + h_у). Ранее мы определили h_у, следовательно:
ρ_вh_в = ρ_рт(h_ш + 5h_ш) или ρ_вh_в = 6ρ_ртh_ш. Найдем h_ш:
h_ш = ρ_вh_в : 6ρ_рт = 1000 • 0,34 : (6 • 13600) = 340 : 81600 = 0,0042 (м) или 0,42 (см).
h_y = 5h_ш = 5 • 0,0042 = 0,021 (м) или 2,1 (см).

Задача № 5. Высота воды в левом колене сообщающихся сосудов h₁ = 40 см, в правом h₂ = 10 см. В каком направлении будет переливаться вода, если открыть кран? На сколько изменится уровень воды в левом сосуде? Найти объем воды, который перелился из одного сосуда в другой. Левое колено сосуда имеет площадь поперечного сечения S₁ = 10 см 2 , правое S = 20 см 2 .

Ответ: в правый; 0,2 м; 0,2 л.

Источник